【C++】实现红黑树，C++实现红黑树算法详解，C++实现红黑树算法详解及操作指南，C++红黑树算法实现详解与操作指南，从基础到进阶的指南，C++红黑树算法实现详解，从基础到进阶的操作指南，C++红黑树算法实现详解，从基础到进阶的操作指南及算法详解，C++红黑树算法实现详解，从基础到进阶的指南与操作手册

摘要：，，本文介绍了C++实现红黑树的算法详解及操作指南。文章从基础概念开始，逐步讲解红黑树的实现方法，包括插入、删除、旋转等基础操作。文章内容丰富，涵盖了从基础到进阶的指南，帮助读者逐步掌握红黑树的实现技巧。通过本文的学习，读者可以深入了解红黑树的算法原理，并能够熟练地进行操作。

本文为您详细解读了红黑树的实现过程，从基本概念、算法详解到操作指南，全方位展示了红黑树的魅力。

红黑树节点结构定义

红黑树由节点构成，每个节点包含键值、颜色信息（红色或黑色）以及指向左右子节点和父节点的指针，颜色是红黑树中的重要属性，对于维持树的平衡起着至关重要的作用。

红黑树的插入操作详解

插入操作是红黑树的核心部分，在插入新节点后，需要进行变色和旋转操作以满足红黑树的性质，具体步骤如下：

1、按照二叉搜索树的插入方式找到要插入的位置。

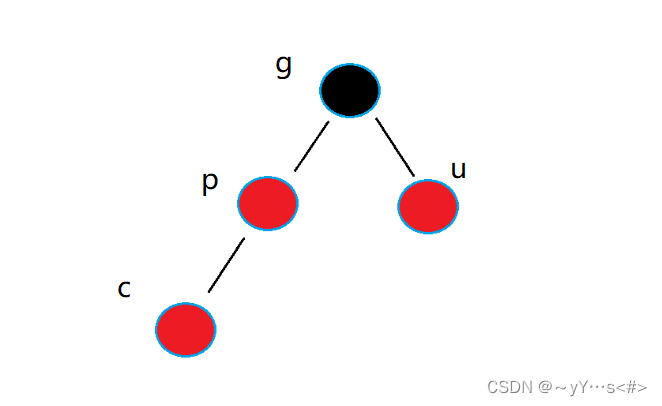
2、插入新节点，并默认将其颜色设置为红色。

3、检查新节点的父节点颜色，如果父节点为黑色，则插入结束；否则，进入变色调整阶段。

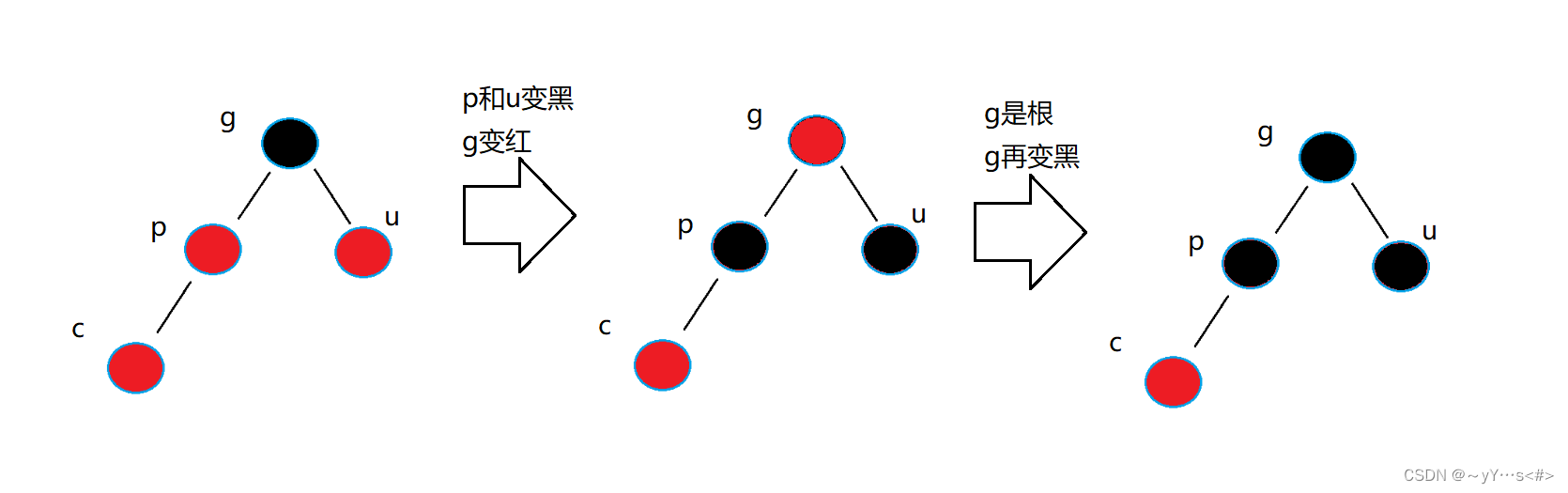
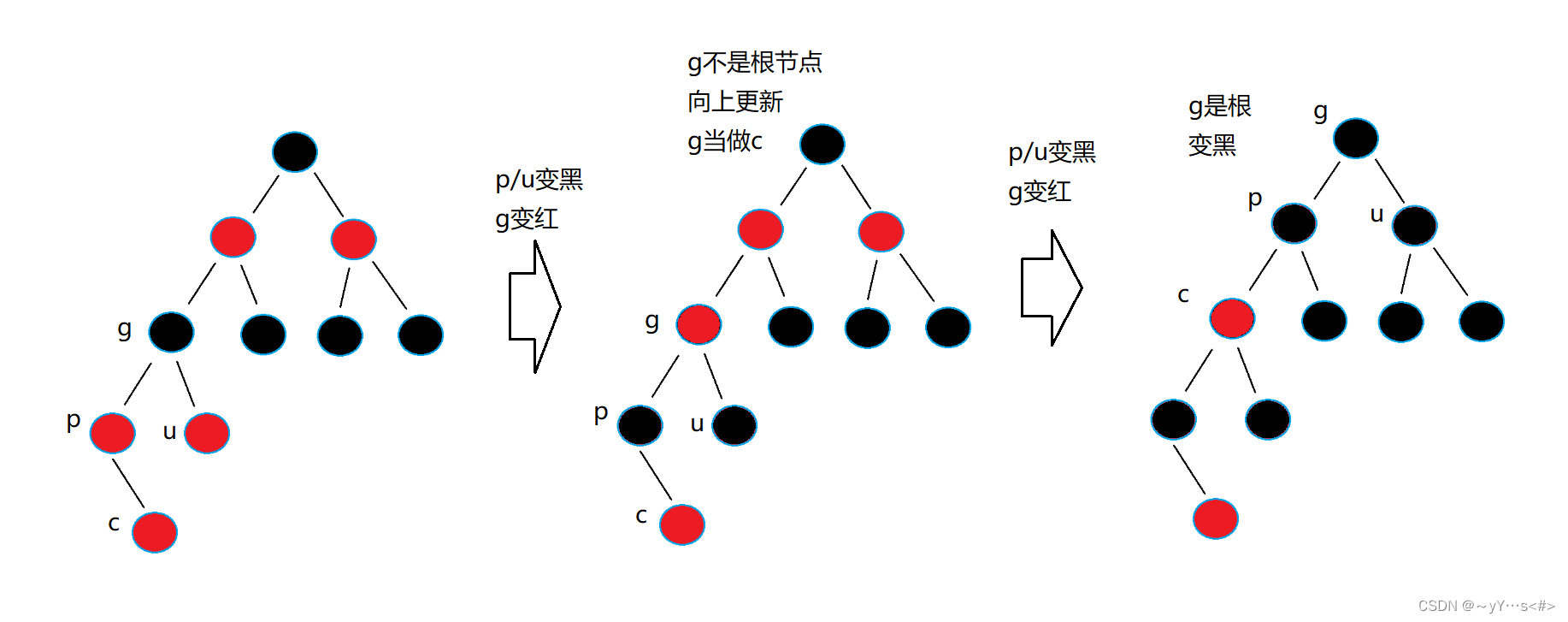
4、根据新节点的父节点和叔叔节点的颜色，进行相应的变色和旋转操作（例如左旋、右旋），确保红黑树的性质得到维护。

红黑树与AVL树的比较

红黑树和AVL树都是平衡二叉树，但它们在平衡方式和实现复杂度上有所不同，AVL树通过比较节点的平衡因子来控制树的平衡，而红黑树则通过控制节点的颜色和路径上的黑色节点数量来保持平衡，相较于AVL树，红黑树的实现相对简单，代码量较小，更容易理解和维护，在实际应用中，红黑树通常更受欢迎。

测试代码及分析的重要性

为了更深入地了解红黑树和AVL树在实际应用中的性能差异，我们进行了以下测试：

1、对比红黑树和AVL树在插入操作时的旋转次数，以评估两者的平衡调整效率。

2、测试两种树在插入操作的时间复杂度，量化性能差异。

3、分析两种树的平衡状态，确保插入新节点后树依然保持平衡。

4、对比两种树的高度，验证红黑树的自平衡特性是否导致更小的树高度。

通过以上测试和分析，我们可以全面评估红黑树和AVL树在实际应用中的性能，为选择合适的平衡二叉树数据结构提供依据，我们还需对红黑树的删除操作进行详细了解与测试，以更全面地评估其性能。

本文旨在为读者提供红黑树的基本原理、实现方法以及实际操作指南，帮助读者逐步掌握红黑树的实现技巧，通过本文的阐述和测试分析，读者可以更加深入地了解红黑树的算法原理和实现细节，同时了解红黑树与AVL树的差异，以便在实际应用中选择合适的平衡二叉树数据结构。——结语部分可以进一步加强和完善，强调红黑树在实际应用中的重要性及其优势。