C++ 素数（质数）的判定方法，C++中素数（质数）的判定方法详解

摘要：C++中素数的判定方法主要是通过遍历待判断数字的每个因子，从2开始到该数字的平方根，检查是否存在能整除该数字的因子。若不存在，则该数字为素数。还可以通过一些优化算法如埃拉托斯特尼筛法、米勒-拉宾素性检验等提高判断效率。这些方法在C++中均可有效实现，用于判断一个数是否为素数。

素数的介绍与判定方法

<div style="text-align:center;"><img style="max-width: 100%;border-radius: 5px;" src="http://www.857vps.cn/zb_users/upload/2024/03/20240327034513171148231323316.png" alt="C++ 素数（质数）的判定方法"></div>（图片来源网络，侵删）

素数的定义：

质数（又称素数）是自然数中无限多的特殊数字，一个大于1的自然数，除了1和它本身以外，不能被其他自然数整除，换句话说，该数除了1和它本身以外不再有其他因数，否则，它被称为合数，根据算术基本定理，每一个大于1的整数，要么本身是质数，要么可以表示为一系列质数的乘积，这种表示形式是唯一的，不考虑这些质数在乘积中的顺序，最小的质数是2。

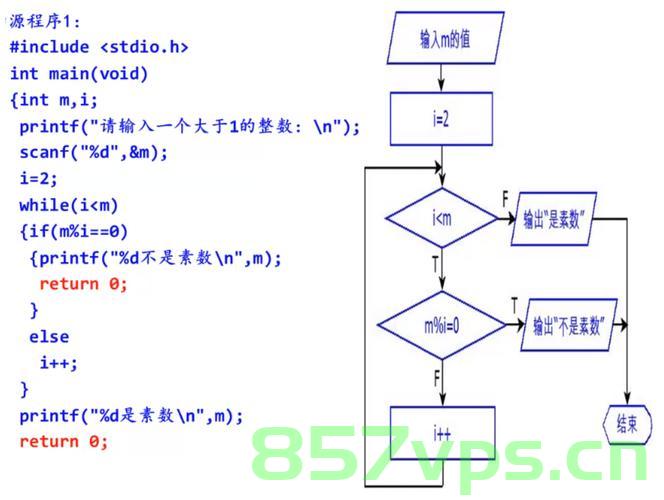
方法一：暴力筛选法

思路：根据素数的定义，判断一个数n是否为素数，可以通过遍历从2到n-1的所有数字，检查是否能被这些数字整除，如果不能被整除，那么n就是素数。

具体实现：

1、从2开始，到n的平方根结束（优化措施，只需检查到根号n即可）。

2、使用循环检查每个数字是否能被n整除。

3、如果找不到能整除n的数字，那么n是素数。

示例代码（C++）：

#include <iostream>
using namespace std;
bool is_prime(int n) {
    if (n <= 1) return false;  // 0和1不是素数
    if (n == 2) return true;   // 2是唯一的偶数素数
    if (n % 2 == 0) return false;  // 排除偶数（除2以外）
    for (int i = 3; i * i <= n; i += 2) {  // 只检查奇数且只需到根号n
        if (n % i == 0) return false;  // 如果n能被i整除，则不是素数
    }
    return true;  // 通过所有检查，是素数
}
int main() {
    int n;  // 需要判断的数值
    cout << "Enter a number: ";  // 提示用户输入数字进行判定是否为素数，后续代码略，请自行补充完整代码逻辑，cin >> n等，然后根据is_prime函数的返回值输出判断结果，cout << (is_prime(n) ? "Prime" : "Not Prime");等，具体输出格式可以根据实际需求调整。}```