代码随想录算法训练营 DAY 20 | 654.最大二叉树 617.合并二叉树 700.二叉搜索树中的搜索 98.验证二叉搜索树，二叉树算法系列训练，最大二叉树、合并与搜索操作及验证二叉搜索树实战解析 DAY 20 代码随想录算法训练营总结报告

摘要：在代码随想录算法训练营的第20天，我们学习了关于二叉树的相关算法。其中包括找到最大二叉树，合并二叉树，以及在二叉搜索树中进行搜索和验证。这些算法涉及对二叉树结构的深入理解和操作，通过学习和实践，我们能更好地掌握二叉树的特性和应用。

最大二叉树

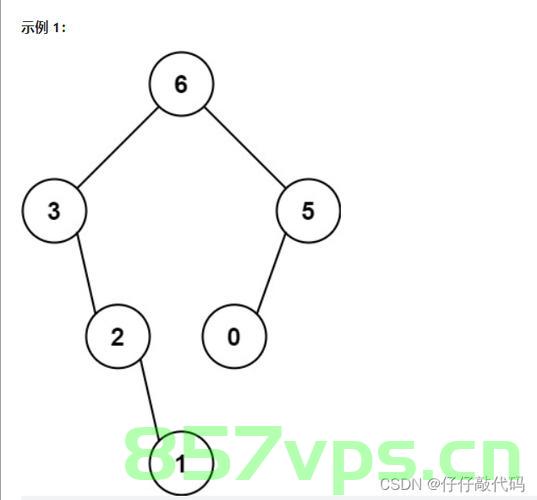
在构造二叉树类的题目中，通常使用前序遍历的方式，即先构造根节点，再构造左子树和右子树，以下是关于最大二叉树的构造方法。

确定递归函数

给定一个数组，我们需要根据这个数组构造一个二叉树，在递归的过程中，每次处理数组的一个子集（即左子树或右子树的节点），递归终止的条件是数组的大小为1，说明已经到达了叶节点。

递归终止条件

当数组的大小为1时，说明已经构造到了叶子节点，此时返回以该值构建的节点，对于题目给定的数组，其大小大于等于1，不考虑空的情况。

单层逻辑

在构造过程中，需要找到数组中的最大值及其索引，根据索引将数组分割成左子树和右子树的节点集合，根据分割后的数组继续构造左子树和右子树，在这个过程中，要确保新构造的左子树和右子树也是最大二叉树。

优化建议

每次递归时都创建新的数组进行分割是不必要的，我们可以使用一个指针来跟踪当前处理的数组段，并在递归过程中更新指针位置，以此避免创建新的数组，这样可以提高算法的效率，以下是优化后的Java代码示例：

合并二叉树

对于合并二叉树的题目，我们需要同时操作两个二叉树，这里使用前序遍历的方式进行处理，以下是合并二叉树的步骤：

递归函数返回值和参数

给定两个二叉树的根节点，我们需要返回合并后的新树的根节点，递归函数的参数是两个根节点。

确定终止条件

当遍历到两个空节点时，返回null作为终止条件，如果一个树为空，则返回另一个树的对应节点作为结果，这是因为在合并过程中，如果一个树为空（即没有节点），那么直接返回另一个树的对应节点即可，如果两个树的对应节点都存在且不为空，则进行合并操作，合并的方式可以是简单的值相加或其他自定义的合并逻辑，这里以简单的值相加为例进行说明，在合并过程中，我们直接在第一个树的结构上进行修改，不重新创建树结构，这样可以避免不必要的内存消耗，完整的Java代码示例如下：首先判断两个根节点是否为空，如果其中一个为空则返回另一个根节点；否则将两个根节点的值相加并更新第一个树的对应节点的值，然后递归地合并左子树和右子树，最后返回第一个树的根节点作为结果，在这个过程中，我们使用了前序遍历的方式进行处理，对于合并操作来说，前序遍历是合适的遍历方式，因为前序遍历的顺序是先访问根节点再访问左右子节点这样可以保证在合并过程中先处理根节点的合并逻辑再处理左右子树的合并逻辑从而得到正确的结果，三、误区提醒陷阱一：不能仅通过比较左节点小于中间节点和右节点大于中间节点来判断是否为二叉搜索树（BST），必须确保左子树的所有节点都小于根节点而右子树的所有节点都大于根节点同时满足这两个条件才能确保是BST，陷阱二：在处理极端情况时需要注意例如最小的整数值可能是int的最小值在这种情况下直接使用最小的int值进行比较可能会导致错误因此可以使用long的最小值Long.MIN_VALUE作为初始比较值以避免这种情况发生，验证二叉搜索树同样可以使用中序遍历来判断一个树是否为BST因为中序遍历的结果是有序的序列如果序列是有序的则说明该树是BST在验证过程中需要注意避免使用简单的比较操作来验证BST的正确性而应该考虑左子树和右子树的验证结果同时确保左子树的所有节点都小于根节点右子树的所有节点都大于根节点这样才能确保验证结果的准确性，Day20总结在解决与二叉搜索树相关的问题时中序遍历是一种非常有用的工具因为它可以帮助我们验证一个树是否为BST以及获取有序序列同时构造二叉树时通常使用前序遍历的方式以确保先构造根节点再构造左右子树。