二项分布假设检验，二项分布假设检验的实践应用与理论探讨，二项分布假设检验的实践应用与理论探讨探索

摘要：本文介绍了二项分布假设检验的相关内容，包括其基本概念、实践应用和理论探讨。文章指出二项分布假设检验是一种统计学方法，用于判断样本数据是否符合二项分布假设。本文详细阐述了二项分布假设检验的应用场景，如质量控制、医学实验等，并探讨了其理论基础和实际操作中的注意事项。文章旨在帮助读者更好地理解和应用二项分布假设检验，为相关领域的研究和实践提供指导。

在概率论与数理统计中，二项分布是一种离散型概率分布，用于描述在n次独立重复试验中成功的次数的概率分布情况，当需要对两组二项分布总体参数的差异性进行推断时，我们进行二项分布的假设检验。

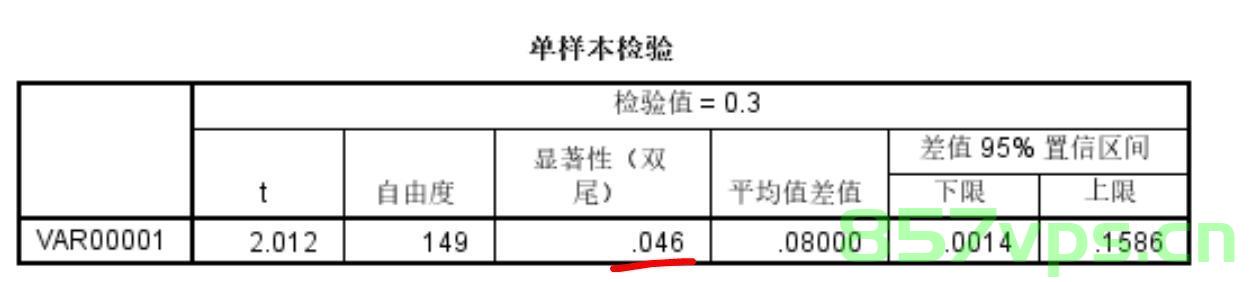
基本定义与性质

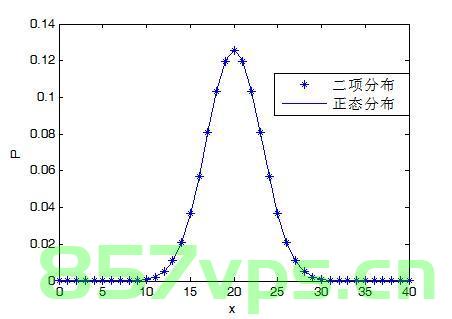
二项分布的概率密度函数为：P(X=k)=nCkpk(1−p)n−kP(X=k) = \binom{n}{k}p^k(1-p)^{n-k}P(X=k)=nCk​pk(1−p)n−k，其中n是试验次数，p是成功的概率，其期望和方差分别为：E(X)=np, Var(X)=np(1−p)E(X)=np, \quad Var(X)=np(1-p)E(X)=np,Var(X)=np(1−p)，当试验次数n很大时，二项分布近似于正态分布。

假设检验的重要性

假设检验是统计推断的重要组成部分，用于判断样本统计量是否足以支持某一假设，在二项分布中，假设检验常用于比较两组数据的差异性，以确定它们是否来自具有不同成功概率的总体。

假设检验步骤与Python实现

步骤：

1、建立原假设和备择假设，原假设H0表示两组数据的成功率相同，备择假设H1表示两组数据的成功率不同，即：H0:p1=p2, H1:p1≠p2H_0: p_1 = p_2, \quad H_1: p_1 \neq p_2H0​:p1​=p2​，H1​:p1​=p2​，其中p1和p2分别是两组数据的成功率。

2、计算估计值和标准误差，估计值是指成功次数的比例，标准误差用于衡量估计值的精确度，对于两组数据，我们需要分别计算这些值，然后计算综合的估计值和标准误差，需要注意的是，我们需要使用加权的方式计算综合值，以考虑每组数据在总体中的比例。

3、计算统计量z，使用公式z=\frac{\hat{p}_1-\hat{p}_2}{se}来计算，hat{p}_i是第i组数据的估计成功率。

4、根据给定的显著性水平α计算P值并进行决策，如果P值小于α，则拒绝原假设；否则接受原假设。

Python实现过程：

from scipy.stats import norm
实际的试验次数和成功次数
n1, n2 = ... # 具体的试验次数和成功次数
x = ... # 综合的成功次数
n = ... # 综合的试验次数
计算估计成功率和标准误差
p_hat = x / n 
se = ... # 计算标准误差的代码 ... 
计算z值和P值
z = (p_hat - p_hat_other) / se 
p_value = 2 * norm.cdf(-abs(z)) 
print("Z-Score:", z) 
print("P-Value:", p_value)

在实际应用中，需要根据具体情况选择合适的统计方法和工具进行数据分析，显著性水平α的选择需要根据实际情况进行确定，通常选择常见的值如α=0.05或α=0.01等，通过二项分布假设检验，我们可以对两组数据的差异性进行科学的推断和决策。