爱上数据结构，二叉树的基本概念，爱上数据结构，二叉树入门解析

摘要：本文将介绍数据结构中的二叉树基本概念。概述二叉树的定义和特点，包括每个节点最多有两个子节点，即左子节点和右子节点。探讨二叉树的遍历方式，如先序遍历、中序遍历和后序遍历等。简要提及二叉树在数据结构中的应用，如搜索、排序和存储等。本文旨在帮助读者理解并爱上数据结构中的二叉树。

🔥个人主页：guoguoqiang. 🔥专栏：数据结构

树的基本概念

1、概念

树是一种非线性的数据结构，由n（n≥0）个有限结点组成，具有层次关系，称之为树是因为它看起来像一棵倒挂的树，即根朝上而叶朝下，没有前驱节点的结点叫做根节点。

在树中，子树不能有交集，否则就是图。

节点的度：一个节点含有的子树的个数称为该节点的度，如上图所示，A的度为6。

叶节点或终端节点：度为0的节点称为叶节点，如上图所示，B、C、H、I等节点为叶节点。

非终端节点或分支节点：度不为0的节点，如上图所示，D、E、F、G等节点为分支节点。

双亲节点或父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点，如上图所示，A是B的父节点。

孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点，如上图所示，B是A的孩子节点。

兄弟节点：具有相同父节点的节点互称为兄弟节点，如上图所示，B、C是兄弟节点。

树的度：一棵树中，最大的节点的度称为树的度，如上图所示，树的度为6。

节点的层次：从根开始定义起，根为第1层，根的子节点为第2层，以此类推。

树的高度或深度：树中节点的最大层次，如上图所示，树的高度为4。

堂兄弟节点：双亲在同一层的节点互为堂兄弟，如上图所示，H、I互为堂兄弟节点。

节点的祖先：从根到该节点所经分支上的所有节点，如上图所示，A是所有节点的祖先。

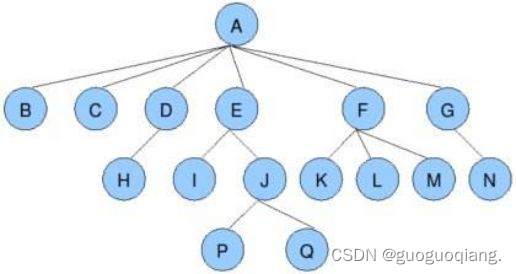
子孙：以某节点为根的子树中任一节点都称为该节点的子孙，如上图所示，所有节点都是A的子孙。

森林：由m（m>0）棵互不相交的树的集合称为森林。

2、树的表示

树的表示通常是通过左孩子右兄弟来表示的。

parent=(child-1)/2;

左孩子=2*parent+1;

右孩子=2*parent+2;

typedef int DataType;

struct Node

struct Node* _firstChild; // 第一个孩子结点

struct Node* _pNextBrother; // 指向其下一个兄弟结点

DataType _data; // 结点中的数据域

};

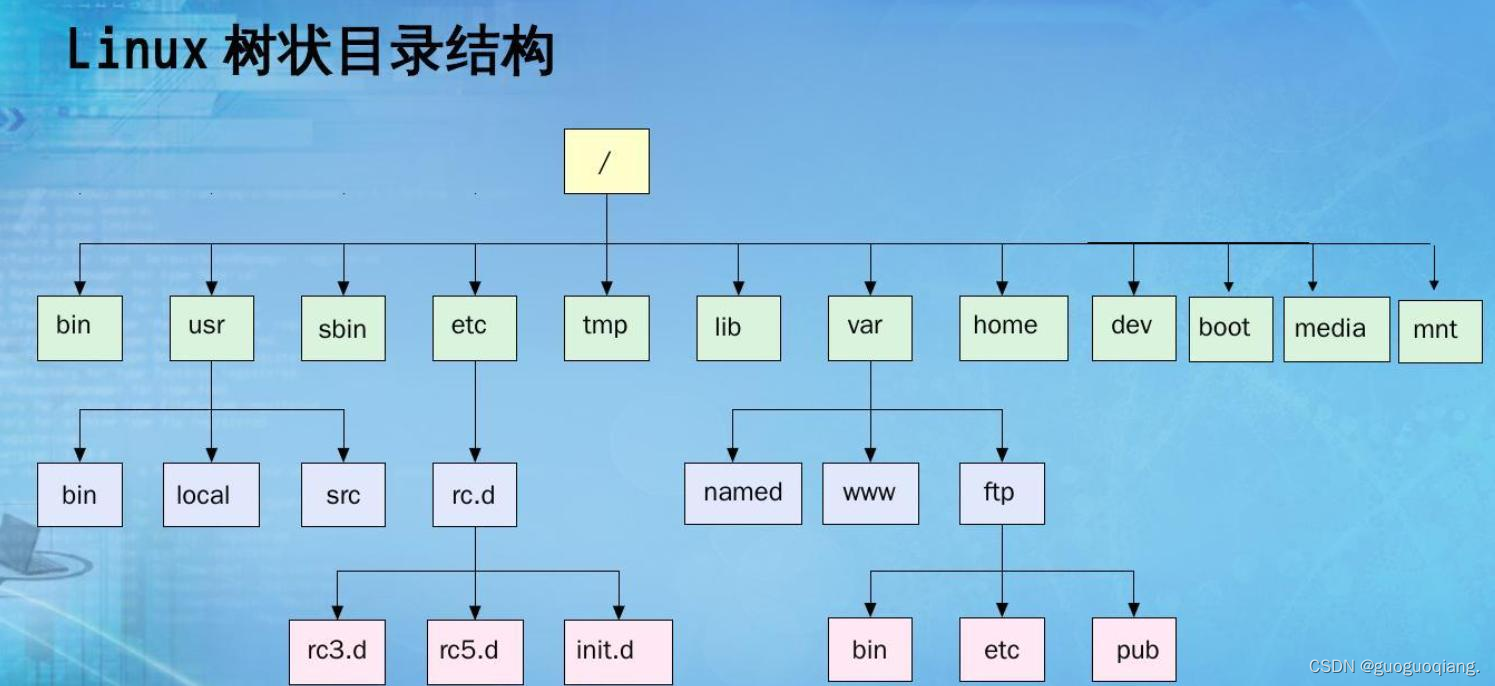
3、树在实际中的应用

（在此插入相关图片）

二叉树的概念及结构

1、二叉树的概念

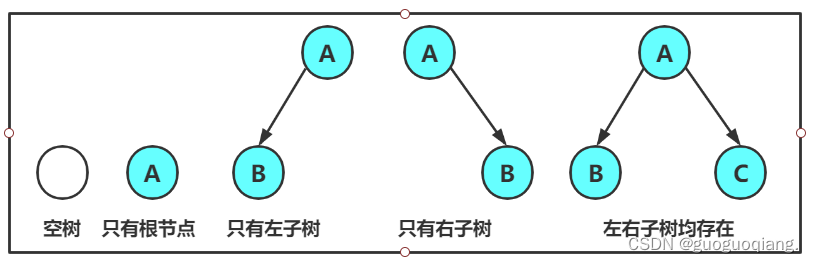
一棵二叉树是结点的一个有限集合，该集合：或者为空，或由根节点加上两棵别称为左子树和右子树的二叉树组成，二叉树是有序树，左子树右子树不能颠倒，二叉树的度不能大于2。

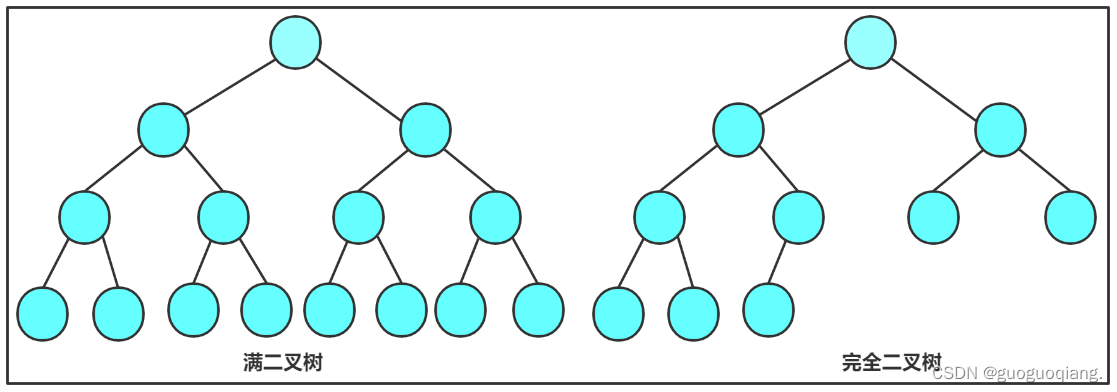
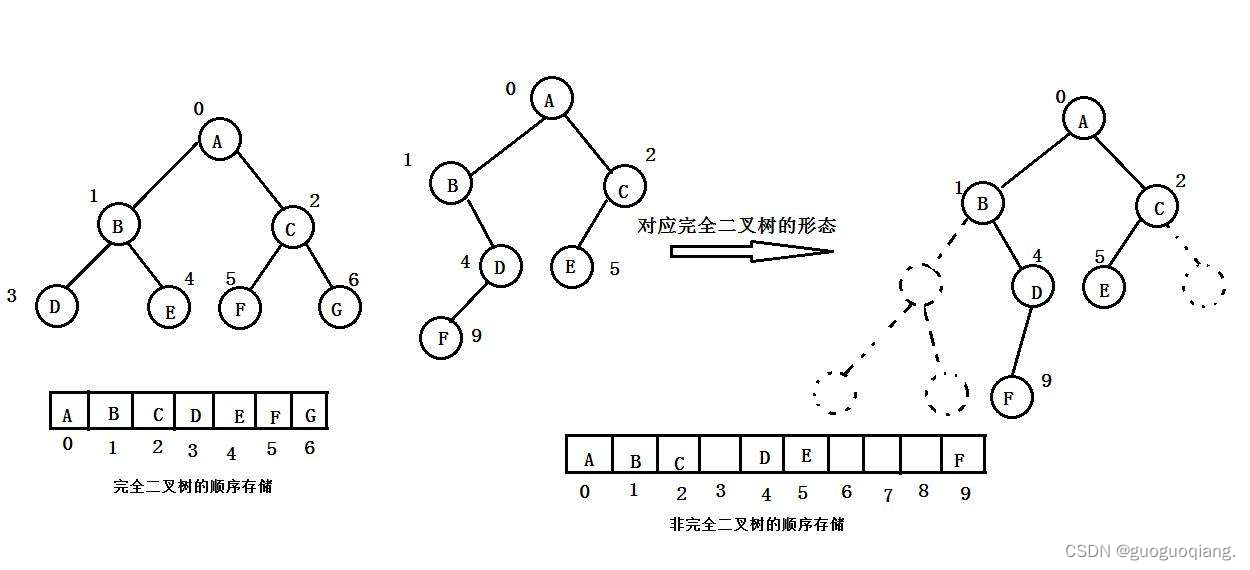
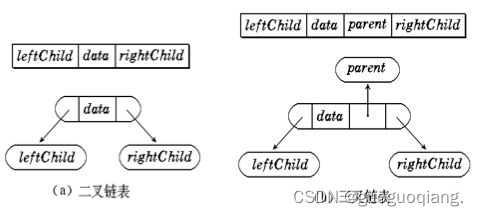
（在此插入相关图片）有两种特殊的二叉树：满二叉树和完全二叉树，对于深度为K的完全二叉树，其结点总数满足特定的条件。（在此插入相关图片）对于深度为K的满二叉树，其每一个层的结点数都达到最大值。（在此插入相关图片）对于深度为K的完全二叉树和满二叉树的性质进行描述和解释。（在此插入相关图片）对于具有特定结点数（例如399个结点）的二叉树的一些性质进行描述和解释。（例如叶子结点数等）对于完全二叉树的性质进行描述和解释。（例如结点数量与高度之间的关系等）对于非完全二叉树的存储结构进行描述和解释。（不适合采用顺序存储结构）对于具有特定结点数的完全二叉树的叶子结点数进行计算。（例如具有特定结点数的完全二叉树的叶子结点数总是等于结点数的一半）对于完全二叉树的存储结构进行描述和解释。（包括顺序存储和链式存储两种结构）顺序存储结构使用数组来存储完全二叉树的特点和公式进行计算。（在此插入相关图片）链式存储结构使用链表来表示一棵二叉树的特点和两种链式存储结构进行描述和解释。（在此插入相关图片展示二叉链和三叉链的结构）代码示例展示二叉链和三叉链的定义和结构，本篇内容到此结束，感谢大家观看！