温馨提示:这篇文章已超过476天没有更新,请注意相关的内容是否还可用!
摘要:第十四届蓝桥杯大赛软件赛省赛(Java 大学A组)是一场面向大学生的编程竞赛,旨在选拔和培养软件领域的优秀人才。该比赛采用Java编程语言,考察参赛者的算法设计、编程实现和问题解决能力。这场比赛为大学生提供了一个展示自己才能的舞台,同时也是提升编程技能、交流学习的好机会。
蓝桥杯 2023年省赛真题
Java 大学A组
试题 A: 特殊日期
试题 B: 与或异或
试题 C: 平均
试题 D: 棋盘
试题 E: 互质数的个数
试题 F: 阶乘的和
试题 G: 小蓝的旅行计划
试题 H: 太阳
试题 I: 高塔
试题 J: 反异或 01 串

那么根据这个夹逼定理我们容易得出湖北经济学院趋近于武大华科。
试题 A: 特殊日期
本题总分:5 分
【问题描述】
记一个日期为 y y \small yy yy 年 m m \small mm mm 月 d d \small dd dd 日,统计从 2000 \small 2000 2000 年 1 \small 1 1 月 1 \small 1 1 日到 2000000 \small 2000000 2000000 年 1 \small 1 1 月 1 \small 1 1 日,有多少个日期满足年份 y y \small yy yy 是月份 m m \small mm mm 的倍数,同时也是 d d \small dd dd 的倍数。
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
35813063
朴素解法
考虑到以日为单位计量,时间段的阶并不大,因此直接使用java.time.LocalDate模拟日期变化,判断然后累加,程序在笔者 P C \rm PC PC 运行 15 15 15 秒后得到了答案。
import java.time.LocalDate;
public class Main {
public static void main(String ...args) { new Main().run(); }
LocalDate start = LocalDate.of(2000, 1, 1);
LocalDate end = LocalDate.of(2000000, 1, 1);
void run() {
long ans = 0;
for (LocalDate i = start; i.compareTo(end) 10x∣yotherwise,对于正整数
y
y
y,记
d
y
d_y
dy为
∑
x
=
1
31
f
y
(
x
)
\sum_{x=1}^{31}f_y(x)
∑x=131fy(x),
m
y
m_y
my为
∑
x
=
1
12
f
y
(
x
)
\sum_{x=1}^{12} f_y(x)
∑x=112fy(x),则在不考虑日期是否合法的情况下,答案为
∑
y
=
2000
2000000
−
1
d
y
m
y
+
1
\sum_{y=2000}^{2000000 - 1} \operatorname{d}_y\operatorname{m}_y+1
∑y=20002000000−1dymy+1。因此我们用倍数法在线性时间复杂度意义下求出
d
d
d 与
m
m
m,将答案拆分成若干合法部分累加,最后得到正确答案。
public static void main(String ...args) { new Main().run(); }
void run() {
System.out.println(
calc(IntStream.rangeClosed(1, 12), IntStream.range(1, 29), y - true)
+ calc(IntStream.of(2), IntStream.of(29), y -> y % 100 == 0 ? (y % 400 == 0) : (y % 4 == 0))
+ calc(IntStream.iterate(1, m -> m == 1 ? 3 : m + 1).limit(11), IntStream.rangeClosed(29, 30), y -> true)
+ calc(IntStream.of(1, 3, 5, 7, 8, 10, 12), IntStream.of(31), y -> true)
+ 1
);
}
final int start = 2000, end = 2000000;
int calc(IntStream m, IntStream d, IntPredicate yf) {
int[] my = new int[end + 1];
int[] dy = new int[end + 1];
m.forEach(
a -> {
for (int i = 1; i * a {
for (int i = 1; i * a my[a] * dy[a]
).sum();
}
}
帅是帅,但放在竞赛中性价比极低,编程多耗费时间都够你针对朴素解法的程序给出好几个测试用例了。
试题 B: 与或异或
本题总分:5 分
【问题描述】
小蓝有一张门电路的逻辑图,如下图所示 : : :
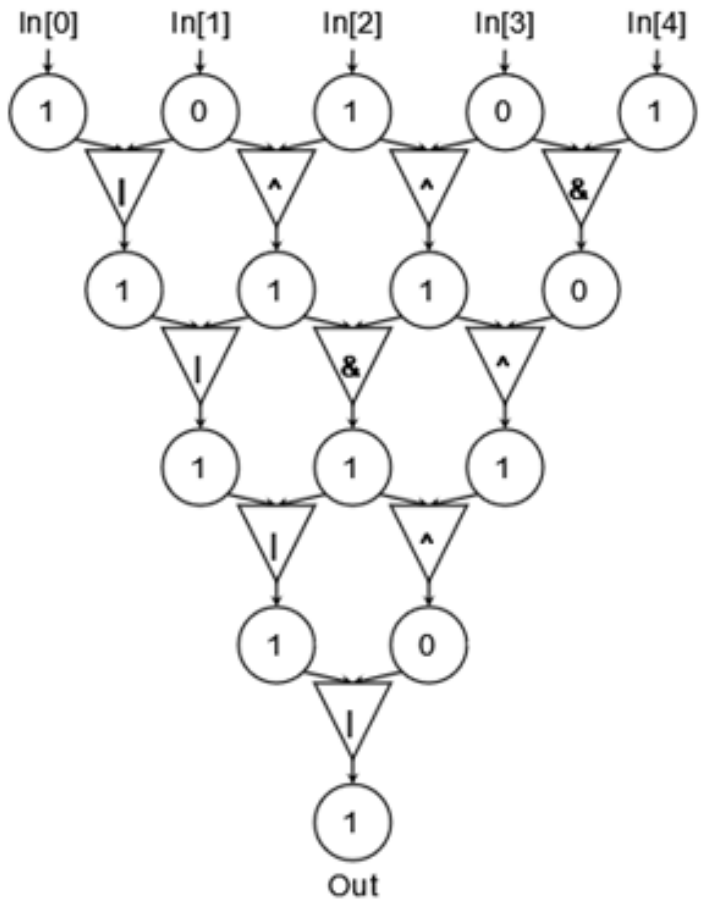
图中每个三角形代表着一种门电路,可能是与门、或门、异或门中的任何一种,它接受上一层中的两个圆形中的数据作为输入,产生一个输出值输出到下一级(如图中箭头所示)。图中圆形表示的是暂存的输出结果,取值只可能是 0 \small 0 0 或 1 \small 1 1,为了便于表示我们用 a r r [ i ] [ j ] \small arr[i][ j] arr[i][j] 表示第 i ( 0 ≤ i ≤ 4 ) \small i(0 ≤ i ≤ 4) i(0≤i≤4) 行第 j ( 0 ≤ j ≤ i ) \small j(0 ≤ j ≤ i) j(0≤j≤i) 个圆形的值。其中 a r r [ 0 ] = ( I n [ 0 ] , I n [ 1 ] , I n [ 2 ] , I n [ 3 ] , I n [ 4 ] ) \small arr[0] = (In[0], In[1], In[2], In[3], In[4]) arr[0]=(In[0],In[1],In[2],In[3],In[4]) 表示的是输入数据,对于某个 a r r [ i ] [ j ] ( i ≤ 0 ) \small arr[i][ j](i ≤ 0) arr[i][j](i≤0),计算方式为 a r r [ i ] [ j ] = a r r [ i − 1 ] [ j ] o p a r r [ i − 1 ] [ j + 1 ] \small arr[i][ j] = arr[i − 1][ j]\ op\ arr[i − 1][ j + 1] arr[i][j]=arr[i−1][j] op arr[i−1][j+1],其中 o p \small op op 表示的是将 a r r [ i − 1 ] [ j ] 、 a r r [ i − 1 ] [ j + 1 ] \small arr[i − 1][ j]、arr[i − 1][ j + 1] arr[i−1][j]、arr[i−1][j+1] 作为输入,将 a r r [ i ] [ j ] \small arr[i][ j] arr[i][j] 作为输出的那个门电路,与门、或门、异或门分别对应于按位与 ( & ) \small (\&) (&)、按位或 ( ∣ ) \small (\:|\:) (∣)、按位异或 ( \small (\, (^ ) \small \,) ) 运算符。
现在已知输入为 I n [ 0 ] = 1 , I n [ 1 ] = 0 , I n [ 2 ] = 1 , I n [ 3 ] = 0 , I n [ 4 ] = 1 \small In[0] = 1, In[1] = 0, In[2] = 1, In[3] = 0, In[4] = 1 In[0]=1,In[1]=0,In[2]=1,In[3]=0,In[4]=1,小蓝想要使得最终的输出 O u t \small Out Out 的值为 1 \small 1 1,请问一共有多少种不同的门电路组合方式?其中上图中显示的就是一种合法的方式。
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
30528
深度优先搜索
暴搜杯!我的青春回来了,开搜!
public class Main {
public static void main(String ...args) { new Main().run(); }
int[][] cir = new int[6][6];
int ans = 0, target = 1;
void run() {
cir[5] = new int[]{ 0, 1, 0, 1, 0, 1 };
dfs(1, 5);
System.out.println(ans);
}
void dfs(int i, int n) {
if (n
if (cir[n][i] == target) ++ans;
} else {
if (i 4;
System.out.println(ans);
}
StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
int nextInt() {
try {
in.nextToken();
} catch (IOException e) {
e.printStackTrace();
}
return (int) in.nval;
}
}
实现上可以将 a i , b i a_i, b_i ai,bi 用一个整形表示,以减少排序的开销,也可以按 a i a_i ai 将 b i b_i bi 分类再依次排序。
试题 D: 棋盘
时间限制:3.0s 内存限制:512.0MB 本题总分:10 分
【问题描述】
小蓝拥有 n × n \small n × n n×n 大小的棋盘,一开始棋盘上全都是白子。小蓝进行了 m \small m m 次操作,每次操作会将棋盘上某个范围内的所有棋子的颜色取反 (也就是白色棋子变为黑色,黑色棋子变为白色)。请输出所有操作做完后棋盘上每个棋子的颜色。
【输入格式】
输入的第一行包含两个整数 n , m \small n, m n,m,用一个空格分隔,表示棋盘大小与操作数。
接下来 m m m 行每行包含四个整数 x 1 , y 1 , x 2 , y 2 \small x_1, y_1, x_2, y_2 x1,y1,x2,y2,相邻整数之间使用一个空格分隔,表示将在 x 1 \small x_1 x1 至 x 2 \small x_2 x2 行和 y 1 \small y_1 y1 至 y 2 \small y_2 y2 列中的棋子颜色取反。
【输出格式】
输出 n \small n n 行,每行 n \small n n 个 0 \small 0 0 或 1 \small 1 1 表示该位置棋子的颜色。如果是白色则输出 0 \small 0 0,否则输出 1 \small 1 1。
【样例输入】
3 3 1 1 2 2 2 2 3 3 1 1 3 3
【样例输出】
001 010 100
【评测用例规模与约定】
对于 30 % \small 30\% 30% 的评测用例, n m ≤ 500 \small n\ m ≤ 500 n m≤500;
对于所有评测用例, 1 ≤ n , m ≤ 2000 , 1 ≤ x 1 ≤ x 2 ≤ n , 1 ≤ y 1 ≤ y 2 ≤ m \small 1 ≤ n, m ≤ 2000,1 ≤ x_1 ≤ x_2 ≤ n,1 ≤ y_1 ≤ y_2 ≤ m 1≤n,m≤2000,1≤x1≤x2≤n,1≤y1≤y2≤m。
二维差分
如果我们用数字的奇偶性来表示黑白棋,用 n × n n\times n n×n 大小且元素全为 0 0 0 的矩阵来表示初始棋盘,容易发现对棋盘 x 1 \small x_1 x1 至 x 2 \small x_2 x2 行和 y 1 \small y_1 y1 至 y 2 \small y_2 y2 列中的棋子颜色取反的操作与对矩阵 x 1 \small x_1 x1 至 x 2 \small x_2 x2 行和 y 1 \small y_1 y1 至 y 2 \small y_2 y2 列中的元素加 1 1 1 的操作等价,我们只需要所有操作结束后的棋盘状态,很典型的二维差分问题。
实现上用到了异或运算在相加上不进位与 0 0 0 和 1 1 1 在 A S C I I \rm ASCII ASCII 相邻的特性。
import java.io.PrintWriter;
import java.io.StreamTokenizer;
import java.io.InputStreamReader;
import java.io.BufferedReader;
import java.io.IOException;
public class Main {
public static void main(String ...args) { new Main().run(); }
byte[][] low = new byte[2002][2002];
void run() {
PrintWriter out = new PrintWriter(System.out);
int n = nextInt(), m = nextInt();
for (int i = 0; i
试题 F: 阶乘的和
时间限制:3.0s 内存限制:512.0MB 本题总分:15 分
【问题描述】
给定
n
\small n
n 个数
A
i
\small A_i
Ai,问能满足
m
!
\small m!
m! 为
∑
i
=
1
n
(
A
i
!
)
\small \sum_{i=1}^n(A_i!)
∑i=1n(Ai!) 的因数的最大的
m
\small m
m 是多少。其中
m
!
\small m!
m! 表示
m
\small m
m 的阶乘,即
1
×
2
×
3
×
⋅
⋅
⋅
×
m
\small 1 × 2 × 3 × · · · × m
1×2×3×⋅⋅⋅×m。
【输入格式】
输入的第一行包含一个整数
n
\small n
n。
第二行包含
n
\small n
n 个整数,分别表示
A
i
\small A_i
Ai,相邻整数之间使用一个空格分隔。
【输出格式】
输出一行包含一个整数表示答案。
【样例输入】
3
2 2 2
【样例输出】
3
【评测用例规模与约定】
对于 40 % \small 40\% 40% 的评测用例, n ≤ 5000 \small n ≤ 5000 n≤5000;
对于所有评测用例, 1 ≤ n ≤ 1 0 5 1 ≤ A i ≤ 1 0 9 \small 1 ≤ n ≤ 10^5\ 1 ≤ A_i ≤ 10^9 1≤n≤105 1≤Ai≤109。
贪心
如果我们尽可能的合并较小的阶乘,直至无法合并,如 2 ! + 2 ! + 2 ! = 3 × 2 ! = 3 ! 2!+2!+2!=3\times2!=3! 2!+2!+2!=3×2!=3!,我们取 3 3 3 作 m m m 一定最优,那么这种策略在任何情况都能受用吗?
首先我们将 A 1 , A 2 , ⋯ , A n A_1, A_2,\cdots,A_n A1,A2,⋯,An 按升序重排,即我们可以一般性假设 i >= 1, r >>= 1) { maxL += mark[l]; maxR += mark[r]; } return Math.max(maxL, maxR); } StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in))); int nextInt() { try { in.nextToken(); } catch (IOException e) { e.printStackTrace(); } return (int) in.nval; } }
试题 H: 太阳
时间限制:3.0s 内存限制:512.0MB 本题总分:20 分
【问题描述】
这天,小蓝在二维坐标系的点 ( X , Y ) \small (X, Y) (X,Y) 上放了一个太阳,看做点光源。
他拿来了 n \small n n 条线段,将它们平行于 x \small x x 轴放置在了坐标系中,第 i \small i i 条线段的左端点在 x i , y i \small x_i, y_i xi,yi,长度为 l i \small l_i li。线段之间不会有重合或部分重合的情况(但可能出现端点相交)。小蓝想知道有多少条线段能被太阳照亮(一条线段有长度大于 0 \small 0 0 的部分被照亮就算)。
【输入格式】
输入的第一行包含三个正整数 n , X , Y \small n, X, Y n,X,Y,相邻整数之间使用一个空格分隔。
接下来 n \small n n 行,第 i \small i i 行包含三个整数 x i , y i , l i \small x_i, y_i, l_i xi,yi,li,相邻整数之间使用一个空格分隔。
【输出格式】
输出一行包含一个正整数表示答案。
【样例输入】
3 10 2000000 5 3 5 6 2 4 0 1 10
【样例输出】
2
【评测用例规模与约定】
对于 30 % \small 30\% 30% 的评测用例, n ≤ 1000 \small n ≤ 1000 n≤1000;
对于所有评测用例, 1 ≤ n ≤ 100000 \small 1 ≤ n ≤ 100000 1≤n≤100000, 0 ≤ x i , X ≤ 1 0 7 \small 0 ≤ x_i, X ≤ 10^7 0≤xi,X≤107, 0 0\\c_1+c_2+\cdots+c_n\leq m}}\prod_{i=1}^nC_i\cdot\prod_{i=1}^nA_i. c1,c2,⋯,cn>0c1+c2+⋯+cn≤m∑i=1∏nAiCi=c1,c2,⋯,cn>0c1+c2+⋯+cn≤m∑i=1∏nCi⋅i=1∏nAi. 记 p ( n , m ) p(n,m) p(n,m) 为 ∑ c 1 , c 2 , ⋯ , c n > 0 c 1 + c 2 + ⋯ + c n ≤ m ∏ i = 1 n C i \sum_{\substack{c_1,c_2,\cdots,c_n > 0\\c_1+c_2+\cdots+c_n\leq m}}\prod_{i=1}^nC_i ∑c1,c2,⋯,cn>0c1+c2+⋯+cn≤m∏i=1nCi。因为在小于 n n n 的回合结束要耗尽能量,所以整理可以知最终答案为: p ( n , m ) ∏ i = 1 n A i + ∑ j = 1 n − 1 ( p ( j , m ) − p ( j , m − 1 ) ) ∏ i = 1 j A i . p(n,m)\prod_{i=1}^nA_i+\sum_{j=1}^{n-1}(p(j,m) -p(j,m-1))\prod_{i=1}^jA_i. p(n,m)i=1∏nAi+j=1∑n−1(p(j,m)−p(j,m−1))i=1∏jAi. 因此该思路下, p ( n , m ) p(n,m) p(n,m) 求解的复杂度与整体直接关联,考虑 p p p 的边界情况,当 n = 1 n=1 n=1 时, p ( 1 , m ) = 1 + 2 + ⋯ + m = m ( m + 1 ) 2 p(1,m) = 1+2+\cdots+m=\cfrac {m(m+1)}2 p(1,m)=1+2+⋯+m=2m(m+1)。考虑 n + 1 n+1 n+1 情况,枚举 C n + 1 C_{n+1} Cn+1 可能的取值 1 , 2 , ⋯ m − n 1,2,\cdots m-n 1,2,⋯m−n,则有递推式: p ( n , m ) = { 1 + 2 + ⋯ + m n = 1 ∑ i = 1 m − n + 1 i p ( i − 1 , m − i ) 1 = 1) { if (b % 2 == 1) res = res * a % mod; a = a * a % mod; } return res; } void run() { int n = nextInt(); long m = nextLong() % mod; long A = 1, p1 = 1, p2 = 1, ans = 0; for (int i = 1; i A = A * nextInt() % mod; p1 = p1 * (m + i) % mod * (m - i + 1) % mod * qpow(2 * i, mod - 2) % mod * qpow(2 * i - 1, mod - 2) % mod; p2 = p2 * (m - 1 + i) % mod * (m - i) % mod * qpow(2 * i, mod - 2) % mod * qpow(2 * i - 1, mod - 2) % mod; if (i == n) p2 = 0; ans = (ans + (p1 - p2) * A) % mod; } System.out.print((ans + mod) % mod); } BufferedReader in = new BufferedReader(new InputStreamReader(System.in)); StringTokenizer token; String next() { while (token == null || !token.hasMoreTokens()) { try { token = new StringTokenizer(in.readLine()); } catch (IOException e) { e.printStackTrace(); } } return token.nextToken(); } int nextInt() { return Integer.parseInt(next()); } long nextLong() { return Long.parseLong(next()); } }






还没有评论,来说两句吧...