图的基本概念辨析,包括连通图、极大连通子图、连通分量、强连通图、极大强连通子图等，图的基本概念辨析，连通图、极大连通子图、连通分量与强连通图解析，图的基本概念辨析，连通图、极大连通子图、连通分量与强连通图的深度解析，深度解析图的基本概念，连通图、极大连通子图、连通分量与强连通图的辨析，图的基本概念辨析，深度解析连通图、极大连通子图、连通分量与强连通图的关系与差异

摘要：本文旨在深度解析图的基本概念，包括连通图、极大连通子图、连通分量与强连通图的辨析。文章详细解释了这些概念的定义和特性，探讨了它们之间的区别与联系。通过深度解析，帮助读者更清晰地理解这些图论中的基本概念，为进一步研究图论相关问题和算法打下坚实的基础。

无向图

1、连通图

连通图是指任意两个顶点之间都存在路径相连的图，在无向图中，如果任意两个顶点都是连通的，那么这张无向图被称为完全连通图。

2、极大连通子图（连通分量）

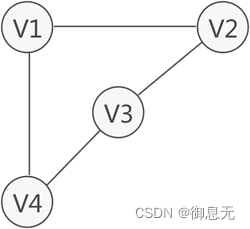
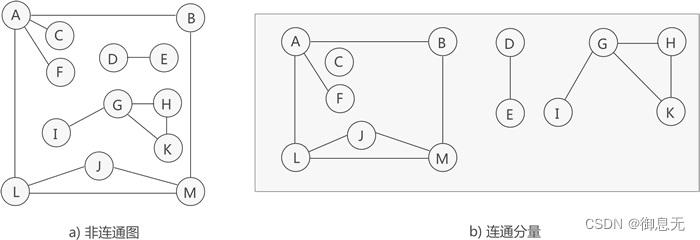
极大连通子图是连通图的子图，包含了原图中的部分顶点和边，且无法通过添加更多顶点或边来增加其连通性，非连通图存在多个极大连通子图，即多个连通分量，这些连通分量是图的基本构成单元。

3、最小连通子图（针对连通图）

最小连通子图是指边最少的连通子图，在一个连通图中，去掉任何一个边都会使其变得不连通，连通图的生成树是一个具有n-1条边的树结构，它是确定的一个最小连通子图，这一概念仅适用于连通图。

有向图

1、强连通图

强连通图是指任意两个顶点之间都存在至少一条双向路径的图，也就是说，从任意一个顶点都可以到达其他任意顶点，并且反之亦然，强连通图是有向图中的特殊类型，具有良好的连通性质。

2、极大强连通子图

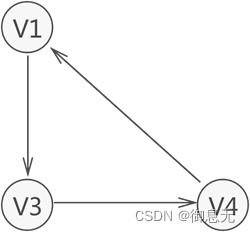
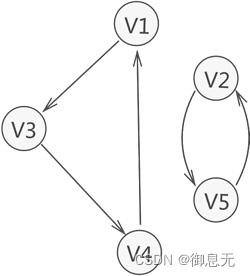
极大强连通子图是有向图的一部分，包含原图中的部分顶点和边，且添加任何更多的顶点或边后不再保持强连通性，它是强连通子图的扩展，具有最大的强连通性。

3、强连通分量（极大强连通子图）

强连通分量是有向图中的极大强连通子图，是该有向图中的一部分，具有最大的强连通性，在强连通图中，所有的顶点都属于同一个强连通分量。

通过对这些概念的清晰辨析，我们能更好地理解和应用图论相关知识，在实际应用中，需要根据具体情况进行理解和应用这些概念，这些概念在图论的研究、算法设计、网络分析等领域有着广泛的应用，对于理解复杂网络和系统具有重要意义。

需要注意的是，本文的资料主要来源于网络，可能存在错误或不完整之处，欢迎读者指正和补充，希望本文能对读者理解图的基本概念有所帮助，同时建议读者通过查阅专业书籍和文献以获取更全面和准确的知识。