Matlab中常见的数据平滑方式，Matlab常见数据平滑方法简介，Matlab常见数据平滑方法与技巧简介

摘要：Matlab中常见的数据平滑方式主要包括移动平均法、指数平滑法、卡尔曼滤波平滑法等多种方法。这些方法能够有效减少数据噪声和波动，提高数据处理的准确性和可靠性。移动平均法通过计算数据点的平均值来平滑数据，指数平滑法则通过加权平均过去和现在的数据点进行平滑处理，卡尔曼滤波平滑法则是一种基于统计模型的平滑方法，能够处理含有噪声和不确定性的数据。这些平滑方法广泛应用于信号处理、图像处理、控制系统等领域。

常见的数据平滑方法包括移动平均、Loess平滑、Savitzky-Golay滤波器、平均平滑（包括指数平滑）、分段线性插值以及小波变换等。

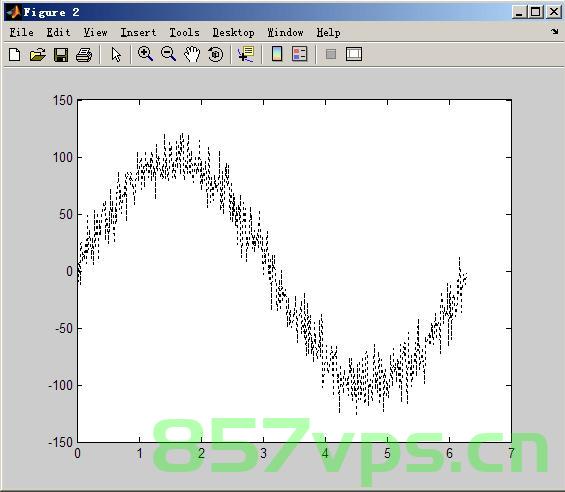
移动平均法

移动平均法是一种简单而有效的数据平滑技术，它通过计算数据窗口内的平均值来减少数据的随机波动，这种方法适用于去除数据的随机噪声，但可能会损失一些高频信息。

Loess平滑

Loess平滑是一种局部加权回归方法，适用于具有趋势和噪声的数据，它能够更好地保留数据的局部特征。

其他方法

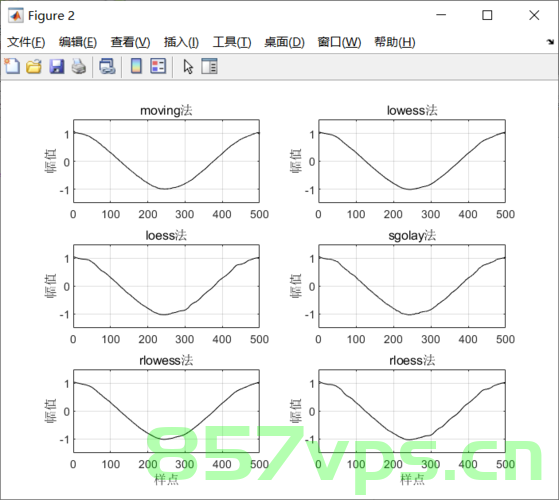
除了上述两种常见方法，MATLAB还提供了许多其他数据平滑方法，Savitzky-Golay滤波器对信号的局部曲线进行拟合，有效地平滑数据并保留信号特征，平均平滑（包括指数平滑）通过计算数据的平均值来减少随机波动，适用于去除噪声，指数平滑还考虑了数据的趋势性，分段线性插值适用于处理稀疏数据或不规则采样数据，通过插值方法对数据点之间的空白进行填充，实现数据的平滑过渡，小波变换则适用于处理具有不同频率成分的信号，能够同时实现空间和时间域的分析。

在实际应用中，选择适合的数据平滑方法和参数是关键，可能需要多次尝试和调整以获得最佳的平滑效果，除了MATLAB内置的函数，还可以考虑使用第三方工具箱或自定义函数来实现更复杂或特定的数据平滑方法。

在选择数据平滑方法时，需要根据数据的特性和需求进行选择和调整，不同的平滑方法适用于不同的场景，请务必根据实际数据进行选择和调整，以获得最佳的平滑效果。