贪心算法|135.分发糖果，贪心算法在糖果分发中的应用

摘要：本文介绍了贪心算法在分发糖果问题中的应用。通过贪心策略，旨在公平合理地分配糖果，使得每个孩子都能获得一定数量的糖果。该算法通过逐步选择局部最优解来解决问题，以达到全局最优解的效果。在分发糖果的过程中，贪心算法能够高效快速地完成任务，提高分发效率。

这道题目要求分发糖果，使得每个孩子的糖果数量与其评分相对应，评分高的孩子获得更多的糖果，解题的关键在于如何遍历以确定每个孩子的糖果数量。

我们可以创建一个与评分大小相同的向量（vector）candyVec，用于记录每个孩子的糖果数量，初始化时，每个孩子的糖果数量都设为1。

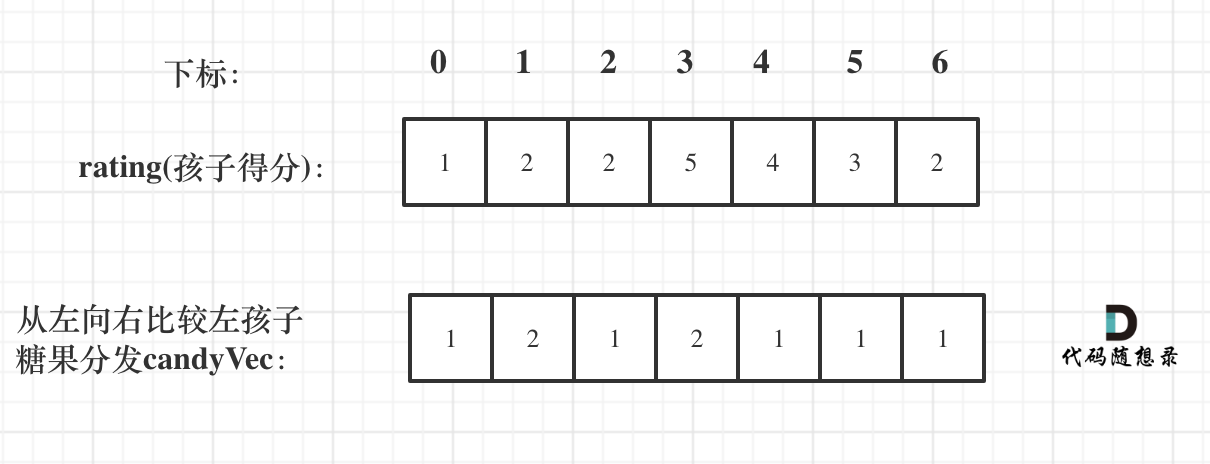
我们从前向后遍历评分数组ratings，如果当前孩子的评分高于前一个孩子的评分，那么当前孩子的糖果数量就应该比前一个孩子的糖果数量多一个，这样，我们可以保证评分高的孩子获得更多的糖果，这个过程可以用以下代码实现：

// 从前向后遍历
for (int i = 1; i < ratings.size(); i++) {
    if (ratings[i] > ratings[i - 1]) {
        candyVec[i] = candyVec[i - 1] + 1;
    }
}

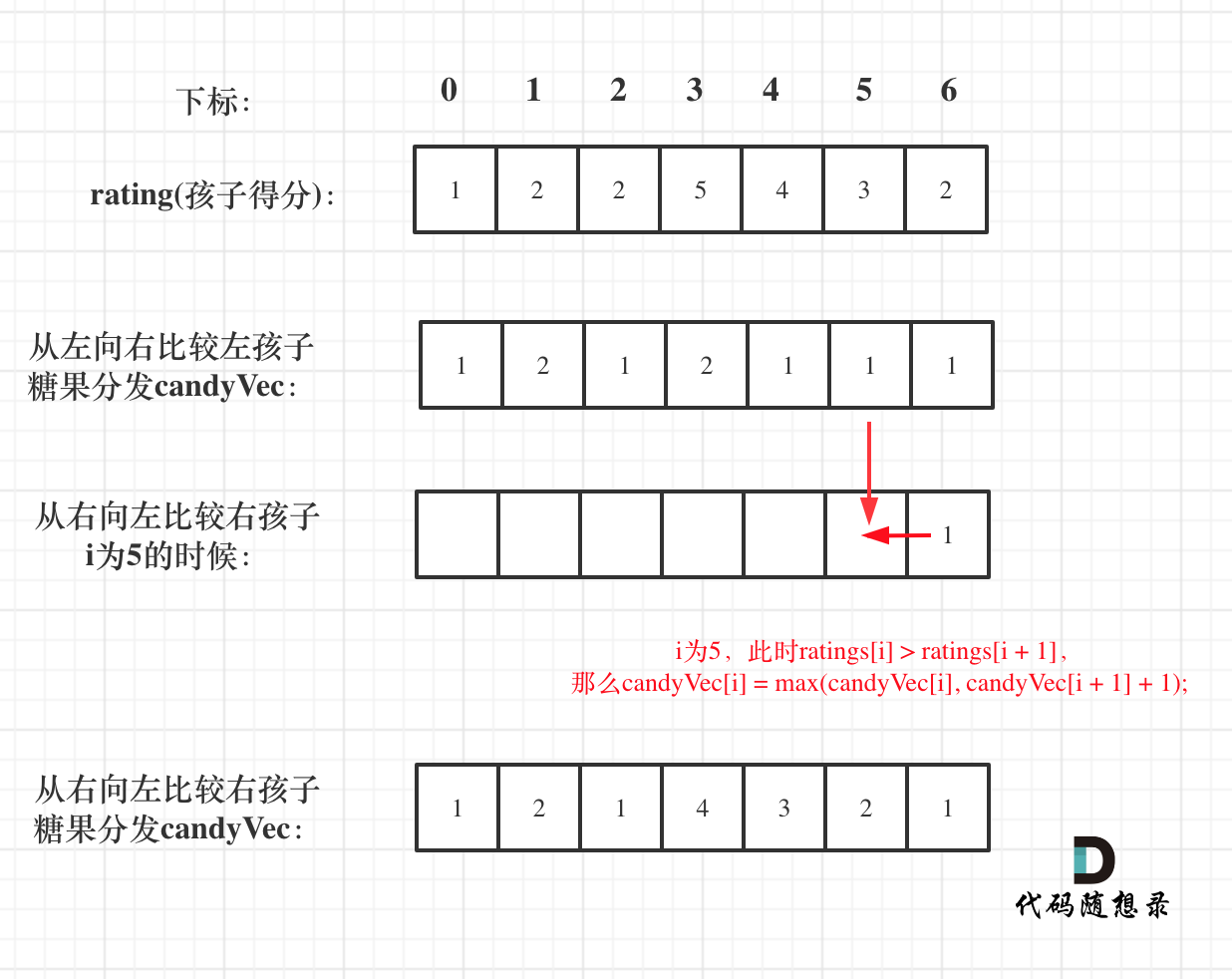
我们从后向前遍历评分数组ratings，如果当前孩子的评分高于后一个孩子的评分，我们需要比较当前孩子的糖果数量与后一个孩子的糖果数量加一的数值，取较大值作为当前孩子的最终糖果数量，这样，我们可以确保相邻的孩子中，评分高的孩子获得更多的糖果，这个过程可以用以下代码实现：

// 从后向前遍历
for (int i = ratings.size() - 2; i >= 0; i--) {
    if (ratings[i] > ratings[i + 1]) {
        candyVec[i] = max(candyVec[i], candyVec[i + 1] + 1);
    }
}

我们统计所有孩子的糖果数量总和，即为最终的结果。

这道题目虽然看起来有些复杂，但只要我们理清思路，按照局部最优推出全局最优的原则，就可以逐步解决问题，通过从前向后和从后向前的两次遍历，我们可以确定每个孩子的糖果数量，使得评分高的孩子获得更多的糖果。