【概率论】正态分布的叠加性和正态分布的标准化，概率论中正态分布的叠加性与标准化探讨

摘要：本文探讨了概率论中的两个重要概念，即正态分布的叠加性和正态分布的标准化。正态分布叠加性指出，多个独立且服从正态分布的随机变量之和仍然服从正态分布，这一性质为统计分析和数据处理提供了便利。而正态分布的标准化则通过转换变量，使其成为服从标准正态分布的随机变量，简化了概率计算。两者共同构成了正态分布理论的基础，广泛应用于各个领域的数据分析和统计研究。

什么是正态分布

正态分布的叠加性

理论：相互独立的正态分布的线性组合仍然服从正态分布，给定两个独立的正态分布X和Y的线性组合的分布。

正态分布标准化

介绍如何通过变换将一般的正态分布转换为标准正态分布，包括具体的变换公式和例子，假设公共汽车门的高度设计问题，如何通过正态分布来解决。

参考文献

列出相关的参考资料，如关于正态分布叠加、正态分布转换为标准正态分布的论文和书籍等。

<h2>一、引言</h2>

<p>正态分布，也被称为高斯分布，是机器学习和深度学习中最常用的概率分布之一，它在VAE模型中的重参技巧、高维数据的处理等都有广泛应用，本文将梳理关于正态分布的相关知识，包括其定义、叠加性、标准化等，并给出相应的参考文献。</p>

<h2>二、什么是正态分布</h2>

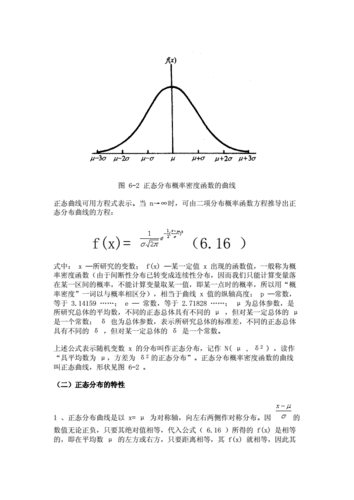
<p>正态分布（Normal distribution），又名高斯分布（Gaussian distribution），若随机变量X的数学期望为μ、方差为σ²，则X的概率密度函数为高斯分布。</p>

<p>一维正态分布的概率密度函数为：</p>

<p>f(x)=1/(σ*sqrt(2*pi)) * exp(-(x-μ)^2/(2*σ^2))</p>

<p>μ决定了其位置，σ决定了其标准差。</p>

<h2>三 3、正态分布的叠加性</h2>

<p>理论：相互独立的正态分布的线性组合仍然服从正态分布。</p>给定两个独立的正态分布X和Y，且a和b为实数，则aX+bY仍然服从正态分布，具体推导过程在此不再赘述，可参见相关文献。

<h2>四、正态分布的标准化</h2>

<p>正态分布是由两个参数μ和σ确定的，任何一个服从N(μ,σ²)分布的随机变量X，都可以通过特定的变换转化为标准正态分布，具体变换公式为：z=(X-μ)/σ，通过此公式，可以将一般正态分布转换为标准正态分布。</p>

<p>假设公共汽车门的高度按成年男性碰头机会小于1%来设计，假设成年男性的身高服从某一正态分布，我们可以通过标准化来计算出合适的车门高度。</p>

<h2>五、参考文献</h2>

<p>[请在此处插入参考文献]</p>

<p>[参考论文或书籍一：关于正态分布的详细定义和性质]</p>

<p>[参考论文或书籍二：关于正态分布叠加的理论推导和实例分析]</p>

<p>[参考论文或书籍三：关于正态分布标准化的详细过程和实例讲解]</p>

<p>[参考博客或论坛帖子等在线资源：关于PRML笔记中关于多维高斯分布的讲解]</p>

仅供参考，如需获取更深入的理解和详细知识，请查阅相关文献和资料。