机器学习和深度学习--李宏毅（笔记与个人理解）Day11-12，机器学习和深度学习--李宏毅教授课程笔记与个人理解 Day11-12概述

摘要：本文介绍了关于机器学习和深度学习的内容，涵盖了李宏毅教授的两天的课程笔记与个人理解。文章指出机器学习是人工智能的一个重要分支，深度学习是其最具代表性的技术之一。通过课程学习，了解到深度学习的基本原理和神经网络结构，包括卷积神经网络和循环神经网络等。文章还涉及了深度学习的应用领域以及未来发展趋势。这些内容对于理解现代人工智能技术的发展和应用具有重要意义。

Day 11 when the gradient is small...

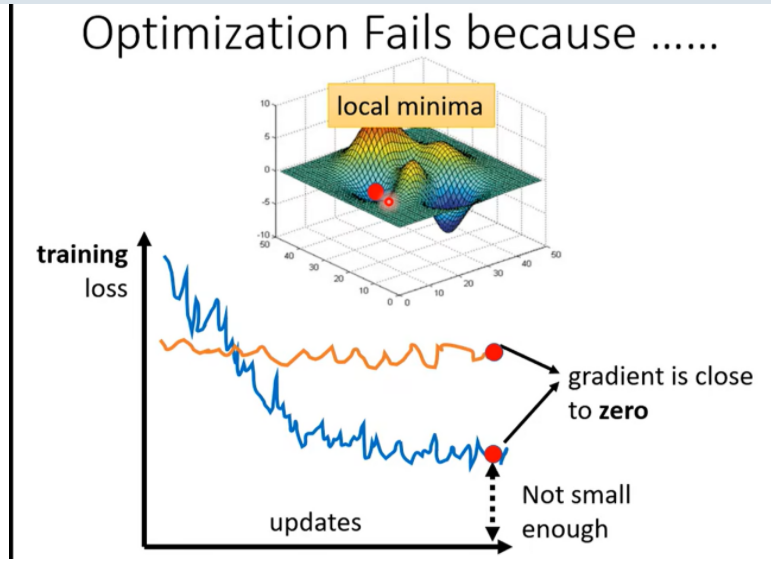
How do we know whether it is a local minimum or a saddle point?

Using Mathematics and the Hessian Matrix, we can determine the concavity of a quadratic function, which indicates whether the point is a minimum, maximum, or saddle point. The Hessian matrix can tell us whether the point is a local minimum or maximum by examining its eigenvalues. If the eigenvalues are all positive, it is a local minimum; if there are both positive and negative eigenvalues, it is a saddle point.

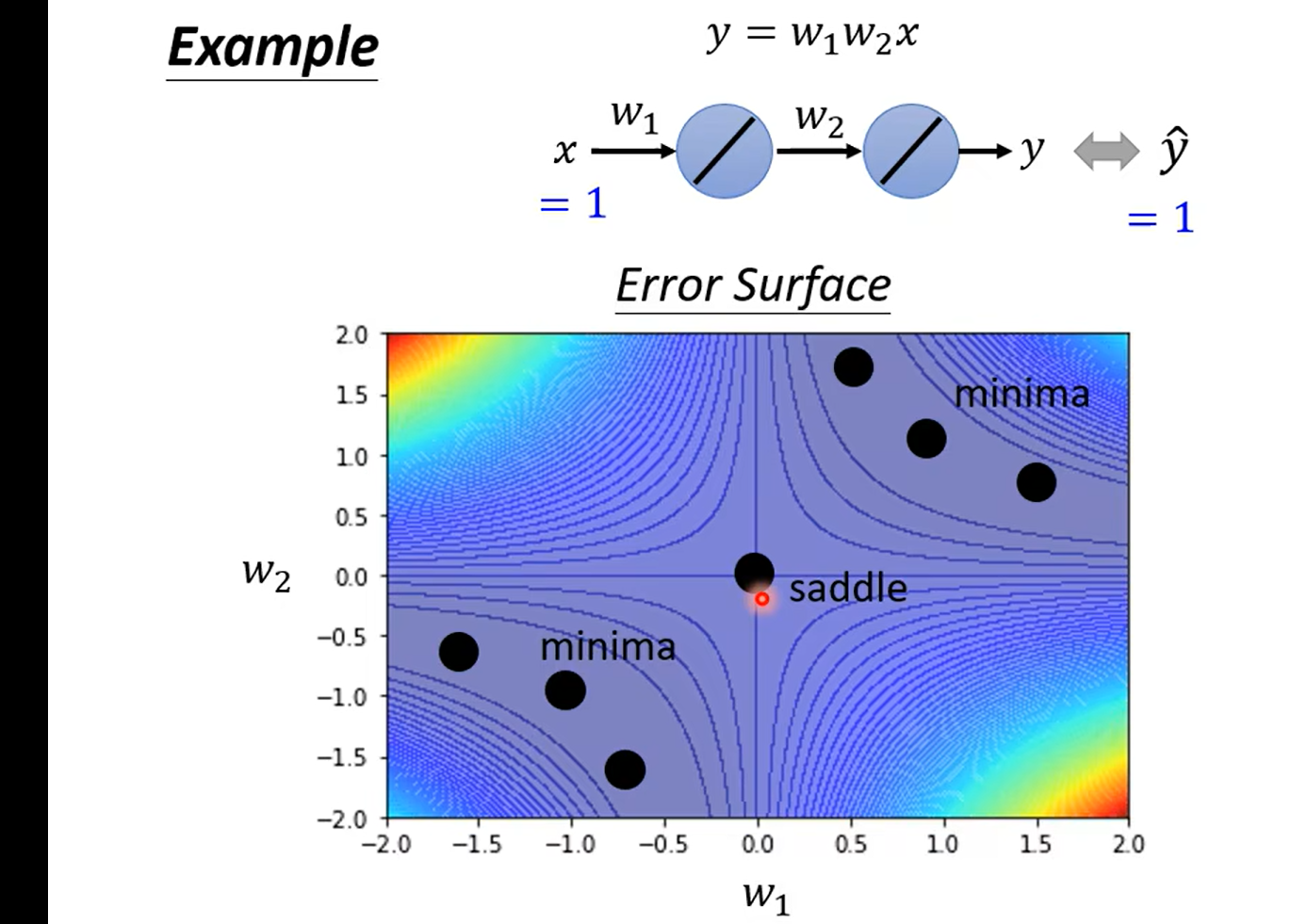
In this example, the Hessian matrix is examined to determine the nature of the critical point. The diagonal elements of the Hessian represent the second derivative of the function along each axis, and their signs determine whether the function is concave or convex at that point.

It's confusing why the main diagonal isn't shown here. In the context of the Hessian matrix, the main diagonal elements represent the second partial derivatives along each axis, and they are crucial for determining the nature of the critical point.

Don't Be Afraid of Saddle Points

Eigenvectorsu and their corresponding eigenvalues λ are defined as vectors and scalars that satisfy the relation Hu=λu. In gradient descent algorithms, we want to choose the direction of θ that minimizes L(θ). If λ (the eigenvalue associated with a particular direction) has a negative value, it means that moving in that direction will increase the value of the function, indicating a saddle point.

Saddle points can be challenging during optimization, but they don't necessarily mean that the optimization process has failed. Understanding how to handle saddle points is crucial for effective optimization in machine learning and other fields.