温馨提示:这篇文章已超过449天没有更新,请注意相关的内容是否还可用!
摘要:数学建模中的评价类模型是用于评估和预测事物性能或结果的定量工具。它运用数学理论和方法,构建反映实际问题的数学模型,通过数据分析与计算,对特定对象进行价值判断或预测其发展趋势。评价类模型广泛应用于各个领域,如经济、金融、教育、环境等,为决策提供科学依据。
目录
一、主观评价
1、层次分析法(AHP)
①应用场景
②步骤
③模型实现
④代码实现
⑤优缺点评价
2、模糊综合评价法(FCE)
①应用场景
②步骤
③模型实现
3、灰色关联分析法(GRA)
①应用场景
②步骤
③模型实现
二、客观评价
1、主成分分析(PCA)
2、因子分析(FA)
①应用场景
②步骤
③模型分析
④代码实现
3、Topsis算法
①应用场景
②步骤
③模型分析
④代码实现
4、BP神经网络综合评价法
①应用场景
②优缺点分析
③代码实现
一、主观评价
1、层次分析法(AHP)
①应用场景
1、最佳方案选取
2、评价类问题
3、指标体系的优选
②步骤
1、将问题条理化、层次化,构造出一个有层次的结构模型。层次分为三层:目标层、准则层、方案层。
2、比较同一层次元素对上一层次同一目标的影响,从而确定它们在目标中所占的比重。采用两两比较的方法,求出他们对于同一个目标的重要性的比例标度,标度等级为1,2,...,9,1/2,1/3,...1/9。得到两两比较判断矩阵。
1--9标度的含义:
1--两个元素同等重要 3--前者稍重要
5--前者明显重要 7--前者强烈重要
9--前者极端重要
2,4,6,8为上述判断的中间值
3、在单一准则下计算元素相对排序权重,以及判断矩阵一致性检验。
4、计算方案层中各元素对于目标层的总排序权重,从而确定首选方案。
③模型实现
题目:对 2017 年各省生态环境与经济交互状况进行合理的评价
应用层次分析法解决问题时,首先要将问题条理化、层次化,构造出一个有层次的结构模型。
这些层次可分为三类:
最高层:经济对环境的影响。
中间层:GDP、人口、地方财政支出、地方财政收入以及居民收支情况。
最底层:严重、轻度、基本无影响。
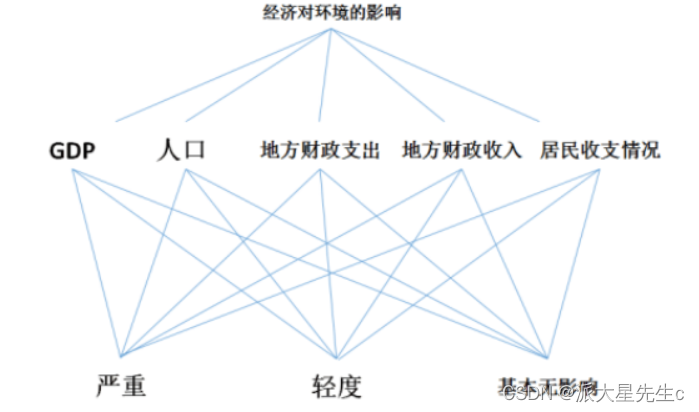
结构图如果所示
建立准则层判断矩阵
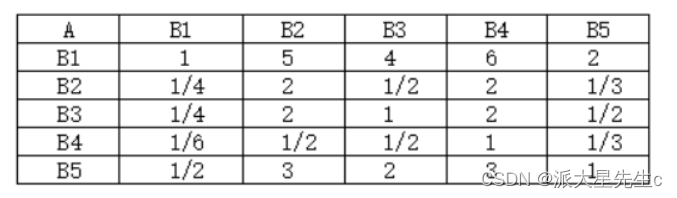
建立方案层判断矩阵

对判断矩阵的一致性检验。
(i)计算一致性指标 CI

(ii)查找相应的平均随机一致性指标 RI 。用随机方法构造 500 个样本矩阵:随机地从 1~9
及其倒 数中抽取数字构造正互反矩阵,求得最大特征根的平均值 max λ',并定义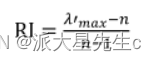
(ⅲ)计算一致性比例 CR
当 CR类似与自变量X
2、对变量进行预处理(去量纲,缩小变量范围,简化计算),先求出每个指标列的均值,再用该指标列的每一个元素都除以该指标列的均值
3、用子序列中每一个元素减去对应母序列中同一行的那个元素,并取绝对值,由此得到一个新矩阵new_X。
4、记a为矩阵中的最小元素,b为矩阵中的最大元素,分辨系数ro通常为0.5,那么每一个元素对应母序列的关联系数为 a+ro*b./(new_X+ro*b)
5、然后,我们再对得到的关联系数矩阵求每一列均值,得到的最后结果gamma就是每一个指标对于母序列的灰色关联度
③模型实现
应用一:分析产业对GDP的影响程度
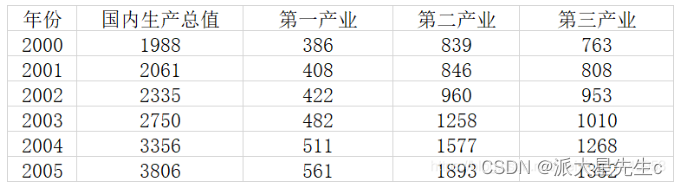
%% 应用一:分析产业对GDP的影响程度
clear;clc;
load data.mat;
r = size(data,1);
c = size(data,2);
%第一步,对变量进行预处理,消除量纲的影响(大家在使用时需要注意自己的数据量纲是否相同)
%avg = repmat(mean(data),r,1);
%data = data./avg;
%定义母序列和子序列
Y = data(:,1); %母序列
X = data(:,2:c); %子序列
Y2 = repmat(Y,1,c-1); %把母序列向右复制到c-1列
absXi_Y = abs(X-Y2)
a = min(min(absXi_Y)) %全局最小值
b = max(max(absXi_Y)) %全局最大值
ro = 0.5; %分辨系数取0.5
gamma = (a+ro*b)./(absXi_Y+ro*b) %计算子序列中各个指标与母序列的关联系数
disp("子序列中各个指标的灰色关联度分别为:");
ans = mean(gamma)
子序列中各个指标的灰色关联度分别为:
ans =
0.7319 0.8983 0.8518 应用二:灰色关联分析评价河流情况
%应用二:灰色关联分析评价河流情况
clear;clc;
load X.mat;
%获取行数列数
r = size(X,1);
c = size(X,2);
%首先,把我们的原始指标矩阵正向化
%第二列中间型--->极大型
middle = input("请输入最佳的中间值:");
M = max(abs(X(:,2)-middle));
for i=1:r
X(i,2) = 1-abs(X(i,2)-middle)/M;
end
%第三列极小型--->极大型
max_value = max(X(:,3));
X(:,3) = abs(X(:,3)-max_value);
%第四列区间型--->极大型
a = input("请输入区间的下界:");
b = input("请输入区间的下界:");
M = max(a-min(X(:,4)),max(X(:,4))-b);
for i=1:r
if (X(i,4)=a)
X(i,4) = 1;
else
X(i,4) = 1-(X(i,4)-b)/M;
end
end
disp("正向化后的矩阵为:");
disp(X);
%把正向化后的矩阵进行预处理,消除量纲的影响
avg = repmat(mean(X),r,1);
new_X = X./avg;
%将预处理后的矩阵每一行的最大值取出,当成母序列(虚构的)
Y = max(new_X,[],2);
%计算各个指标和母序列的灰色关联度
%先把new_X矩阵所有元素都减去母序列中同行的元素,并取绝对值
Y2 = repmat(Y,1,c);
new_X = abs(new_X-Y2);
a = min(min(new_X)); %全矩阵最小值
b = max(max(new_X)); %全矩阵最大值
ro = 0.5;
new_X = (a+ro*b)./(new_X+ro*b);
disp("各个指标对于母序列的灰色关联度为:");
gamma = mean(new_X)
%计算各个指标的权重
disp("各个指标的权重为:");
weight = gamma./(sum(gamma,2))
%-------------------------------------------------------------------------------------------------------
%继续TOPSIS的步骤:对正向化后的矩阵X进行标准化(原矩阵除以每一列元素平方之和的开方)
temp1 = X.*X; %先让每每一个元素平方
temp2 = sum(temp1); %再对每一列求和
temp3 = temp2.^0.5; %再把结果开方
temp4 = repmat(temp3,r,1); %把开方后的结果按行复制r行
disp("******标准化后的矩阵为:");
Z = X./temp4 %原矩阵除以每一列元素平方之和的开方
Z_max = max(Z) %获得Z每一列中最大的元素
Z_min = min(Z) %获得Z每一列中最小的元素
D_max = sum(weight.*(Z-repmat(Z_max,r,1)).^2,2).^0.5
D_min = sum(weight.*(Z-repmat(Z_min,r,1)).^2,2).^0.5
disp("该矩阵得分为:")
S = D_min./(D_max+D_min)
disp("矩阵归一化后得分为:");
S = S./(repmat(sum(S),r,1))
输出结果为:
请输入最佳的中间值:7
请输入区间的下界:10
请输入区间的上界:20
正向化后的矩阵为:
4.6900 0.7172 3.0000 1.0000
2.0300 0.4069 35.0000 0.6940
9.1100 0.5241 8.0000 0.9058
8.6100 0.9655 8.0000 0.4443
7.1300 0.6552 4.0000 0.6914
2.3900 0.8414 16.0000 0.6007
7.6900 0.8552 16.0000 0.6551
9.3000 0.8690 27.0000 0
5.4500 0.5724 49.0000 1.0000
6.1900 0.8138 37.0000 0.7848
7.9300 0.6345 45.0000 0.6992
4.4000 0.8069 37.0000 0.5419
7.4600 0.1448 31.0000 1.0000
2.0100 0 7.0000 0.4546
2.0400 0.5862 31.0000 1.0000
7.7300 0.4069 2.0000 1.0000
6.3500 0.6000 29.0000 0.1824
8.2900 0.0276 15.0000 1.0000
3.5400 0.8138 0 0.4088
7.4400 0.4897 46.0000 0.2731
new_X =
0.7831 1.2228 0.1345 1.4997
0.3390 0.6937 1.5695 1.0408
1.5211 0.8936 0.3587 1.3584
1.4376 1.6461 0.3587 0.6662
1.1905 1.1170 0.1794 1.0369
0.3991 1.4345 0.7175 0.9008
1.2840 1.4580 0.7175 0.9825
1.5528 1.4815 1.2108 0
0.9100 0.9759 2.1973 1.4997
1.0336 1.3874 1.6592 1.1769
1.3241 1.0817 2.0179 1.0486
0.7347 1.3757 1.6592 0.8127
1.2456 0.2469 1.3901 1.4997
0.3356 0 0.3139 0.6818
0.3406 0.9994 1.3901 1.4997
1.2907 0.6937 0.0897 1.4997
1.0603 1.0229 1.3004 0.2735
1.3842 0.0470 0.6726 1.4997
0.5911 1.3874 0 0.6131
1.2423 0.8348 2.0628 0.4096
Y2 =
1.4997 1.4997 1.4997 1.4997
1.5695 1.5695 1.5695 1.5695
1.5211 1.5211 1.5211 1.5211
1.6461 1.6461 1.6461 1.6461
1.1905 1.1905 1.1905 1.1905
1.4345 1.4345 1.4345 1.4345
1.4580 1.4580 1.4580 1.4580
1.5528 1.5528 1.5528 1.5528
2.1973 2.1973 2.1973 2.1973
1.6592 1.6592 1.6592 1.6592
2.0179 2.0179 2.0179 2.0179
1.6592 1.6592 1.6592 1.6592
1.4997 1.4997 1.4997 1.4997
0.6818 0.6818 0.6818 0.6818
1.4997 1.4997 1.4997 1.4997
1.4997 1.4997 1.4997 1.4997
1.3004 1.3004 1.3004 1.3004
1.4997 1.4997 1.4997 1.4997
1.3874 1.3874 1.3874 1.3874
2.0628 2.0628 2.0628 2.0628
new_X =
0.7166 0.2769 1.3651 0
1.2306 0.8758 0 0.5287
0 0.6275 1.1624 0.1627
0.2085 0 1.2873 0.9799
0 0.0735 1.0111 0.1536
1.0354 0 0.7170 0.5336
0.1739 0 0.7405 0.4755
0 0.0714 0.3421 1.5528
1.2873 1.2214 0 0.6976
0.6256 0.2718 0 0.4823
0.6938 0.9362 0 0.9693
0.9245 0.2835 0 0.8465
0.2541 1.2528 0.1095 0
0.3462 0.6818 0.3679 0
1.1591 0.5003 0.1095 0
0.2090 0.8060 1.4100 0
0.2402 0.2775 0 1.0270
0.1155 1.4526 0.8270 0
0.7963 0 1.3874 0.7743
0.8205 1.2280 0 1.6532
各个指标对于母序列的灰色关联度为:
gamma =
0.6665 0.6800 0.7052 0.6880
各个指标的权重为:
weight =
0.2433 0.2482 0.2574 0.2511
******标准化后的矩阵为:
Z =
0.1622 0.2483 0.0245 0.3065
0.0702 0.1408 0.2863 0.2127
0.3150 0.1814 0.0655 0.2776
0.2977 0.3342 0.0655 0.1361
0.2466 0.2268 0.0327 0.2119
0.0826 0.2912 0.1309 0.1841
0.2659 0.2960 0.1309 0.2008
0.3216 0.3008 0.2209 0
0.1885 0.1981 0.4009 0.3065
0.2141 0.2817 0.3027 0.2405
0.2742 0.2196 0.3682 0.2143
0.1522 0.2793 0.3027 0.1661
0.2580 0.0501 0.2536 0.3065
0.0695 0 0.0573 0.1393
0.0705 0.2029 0.2536 0.3065
0.2673 0.1408 0.0164 0.3065
0.2196 0.2077 0.2373 0.0559
0.2867 0.0095 0.1227 0.3065
0.1224 0.2817 0 0.1253
0.2573 0.1695 0.3763 0.0837
Z_max =
0.3216 0.3342 0.4009 0.3065
Z_min =
0.0695 0 0 0
D_max =
0.2109
0.1739
0.1870
0.1907
0.2034
0.1920
0.1506
0.1794
0.0944
0.0841
0.0788
0.1231
0.1631
0.2839
0.1587
0.2192
0.1708
0.2153
0.2448
0.1427
D_min =
0.2028
0.1934
0.2081
0.2148
0.1787
0.1844
0.2137
0.2247
0.2795
0.2508
0.2619
0.2270
0.2223
0.0756
0.2244
0.1952
0.1774
0.1974
0.1559
0.2322
该矩阵得分为:
S =
0.4902
0.5265
0.5266
0.5297
0.4677
0.4899
0.5866
0.5559
0.7476
0.7489
0.7686
0.6483
0.5768
0.2104
0.5857
0.4710
0.5095
0.4782
0.3891
0.6194
矩阵归一化后得分为:
S =
0.0449
0.0482
0.0482
0.0485
0.0428
0.0448
0.0537
0.0509
0.0684
0.0685
0.0703
0.0593
0.0528
0.0193
0.0536
0.0431
0.0466
0.0438
0.0356
0.0567
参考文章:http://t.csdn.cn/46ibb
二、客观评价
1、主成分分析(PCA)
可以参考我之前总结的文章《数学建模--数据预处理》
http://t.csdn.cn/xuWmO
主成分分析是一种降维算法,它能将多个指标转换为少数几个主成分,这些主成分是原始变量的线性组合,且彼此之间互不相关,其能反映出原始数据的大部分信息。一般来说,当研究的问题涉及到多变量且变量之间存在很强的相关性时,我们可考虑使用主成分分析的方法来对数据进行简化。
2、因子分析(FA)
①应用场景
减少分析变量个数
通过对变量间相关关系的探测,将原始变量分组,即将相关性高的变量分为一组,用共性因子来代替该变量
使问题背后的业务因素的意义更加清晰呈现
②步骤
1、选择分析的变量
2、计算所选原始变量的相关系数矩阵
3、提取公共因子
4、因子旋转
5、计算因子得分
③模型分析
以废气排放为例说明主成分降维处理过程
1、评价标准体系的构建
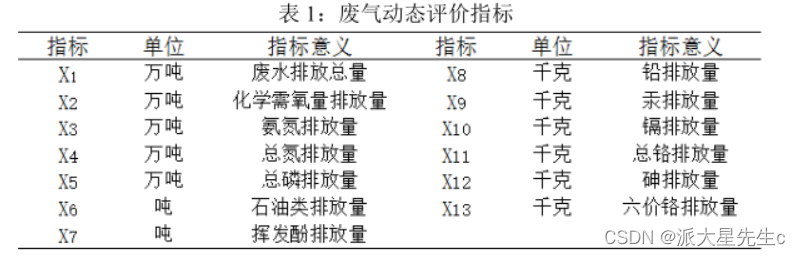
2、因子分析
因子分析首先将原始数据标准化处理,建立相关系数矩 阵并计算其特征值和特征向量,接着从中选择特征值大于等 于1的特征值个数为公共因子数,或者根据因子对X的累计贡献 率大于80%来确定公共因子,求得因子载荷矩阵, 后计算公因子得分和综合得分。
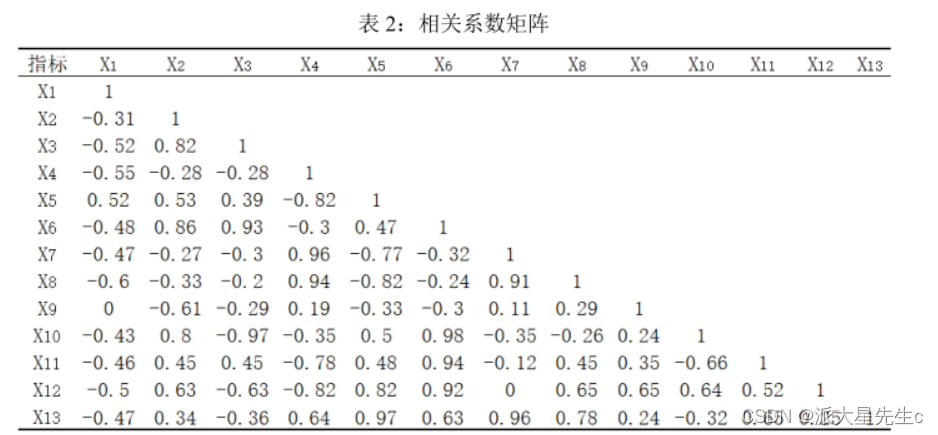
观察相关系数矩阵表 2,可以发现所选取指标之间存在着一定的相关关系,其中 X3 和 X6、X4 和
X7、 X7 和 X8 分别存在着较强的相关性,相关系数分别为 0.96、 0.96、0.91,这进一步验证了对所选指标做因子分析的科学性和必要性。计算相关系数矩阵的特征值、贡献率及累计贡献率如
所示:
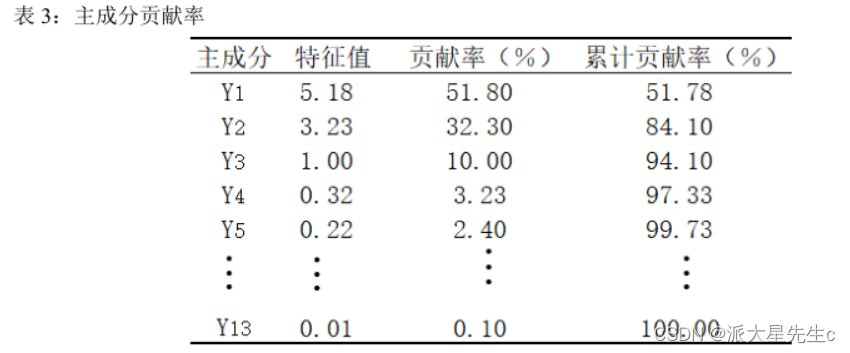
确定提取的主成分个数可综合考虑 3 个方面:
(1)提取的所有特征值大于某一特定特征值,一般特定值设为 1,本文同样以 1 为标准;
(2) 提取的主成分的累计贡献率要大于 85%,即所提取的主成分要能够概括原有指标的绝大部分信息; 由表 3 可知,前 3 个主成分的累计贡献率已经达到了94.01%,满足按照累计贡献率大于 85% 确定主成分个数的原则;
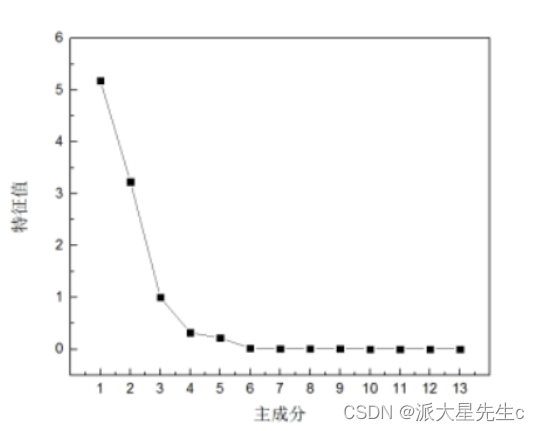
(3) 以做主成分分析时生成的碎石图 (Scree Plot) 做参考,碎石图是按照特征值大小排列的,以特征值为纵坐标、因子数为横坐标生成的主成分散点图,有明显的拐点,一般取拐点前所有的因子及拐点后第一个因子作为主成分 。
观察图 4 可得,第一、第二个主成分的特征值较大,其余几个均较小,碎石图在第三个特征值出现
拐点。
根据上述分析,在本研究中选取前 3 个主成分对河南省水资源使用情况进行动态分析,从表 3
和 4,我们可以看出前 3 个主成分已经能够概括绝大部分的原始信息,因此提取 3 个主成分因子是
合理的. 提取 3 个主成分用于概括原有 10 个指标的绝大部分信息,这既达到了降维、简化的目的,又在一定程度上保证了后续研究结果能准确有效地反映出河南省水资源使用情况动态变化的基本特征。计算主成分的载荷矩阵, 主成分载荷是指提取的 3 大主成分与各变量指标之间的相关系数如表4:

④代码实现
clc,clear
r=[1.000 0.577 0.509 0.387 0.462
0.577 1.000 0.599 0.389 0.322
0.509 0.599 1.000 0.436 0.426
0.387 0.389 0.436 1.000 0.523
0.462 0.322 0.426 0.523 1.000];
%下面利用相关系数矩阵求主成分解,val的列为r的特征向量,即主成分的系数
[vec,val,con]=pcacov(r);%val为r的特征值,con为各个主成分的贡献率
f1=repmat(sign(sum(vec)),size(vec,1),1); %构造与vec同维数的元素为±1的矩阵
vec=vec.*f1; %修改特征向量的正负号,每个特征向量乘以所有分量和的符号函数值
f2=repmat(sqrt(val)',size(vec,1),1);
a=vec.*f2 %构造全部因子的载荷矩阵
a1=a(:,1) %提出一个因子的载荷矩阵
tcha1=diag(r-a1*a1') %计算一个因子的特殊方差
a2=a(:,[1,2]) %提出两个因子的载荷矩阵
tcha2=diag(r-a2*a2') %计算两个因子的特殊方差
ccha2=r-a2*a2'-diag(tcha2) %求两个因子时的残差矩阵
gong=cumsum(con) %求累积贡献率
clc,clear
load data.txt; %把原始数据保存在纯文本文件data.txt中
n=size(data,1);
x=data(:,1:4); y=data(:,5); %分别提出自变量x和因变量y的值
——————————————————————————————————
如果不需要检验,则不需要把y列入原始数据中,把矩阵x的大小改变一下,以及下文中的m,m为原始数据中变量的个数。
——————————————————————————————————
m=4;%m为变量的个数
x=zscore(x); %数据标准化
r=cov(x); %求标准化数据的协方差阵,即求相关系数矩阵
[vec,val,con]=pcacov(r); %进行主成分分析的相关计算
c=cumsum(con);
i=1;
while ((c(i)10))
i=i+1;
end
num=i;
f1=repmat(sign(sum(vec)),size(vec,1),1);
vec=vec.*f1; %特征向量正负号转换
f2=repmat(sqrt(val)',size(vec,1),1);
a=vec.*f2; %求初等载荷矩阵
am=a(:,1:num); %提出num个主因子的载荷矩阵
[b,t]=rotatefactors(am,'method', 'varimax'); %旋转变换,b为旋转后的载荷阵
bt=[b,a(:,num+1:end)]; %旋转后全部因子的载荷矩阵
contr=sum(bt.^2); %计算因子贡献
rate=contr(1:num)/sum(contr); %计算因子贡献率
fprintf('综合因子得分公式:F=');
for i=1:num
fprintf('+%f*F%d',rate(i),i);
end
fprintf('\n');
coef=inv(r)*b; %计算得分函数的系数
coef=coef';
for i=1:num
fprintf('各个因子得分函数为F%d=',i);
for j=1:m
fprintf('+(%f)*x_%d',coef(i,j),j);
end
fprintf('\n');
end
%如果仅仅因子分析,程序到此为止
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
score=x*coef';%计算各个因子的得分
weight=rate/sum(rate); %计算得分的权重
Tscore=score*weight'; %对各因子的得分进行加权求和,即求各企业综合得分
[STscore,ind]=sort(Tscore,'descend'); %对企业进行排序
display=[score(ind,:)';STscore';ind']; %显示排序结果
fprintf('排序结果如下:');
for i=1:num
fprintf('第%d行为F%d得分,',i,i);
end
fprintf('第%d行为综合因子得分,第%d为原序列\n',num+1,num+2);
disp(display);
[ccoef,p]=corrcoef([Tscore,y]); %计算F与资产负债的相关系数
[d,dt,e,et,stats]=regress(Tscore,[ones(n,1),y]);%计算F与资产负债的方程
fprintf('因子分析法的回归方程为:F=%f+(%f*y)',d(1),d(2));
if (stats(3)





还没有评论,来说两句吧...