温馨提示:这篇文章已超过454天没有更新,请注意相关的内容是否还可用!
摘要:在2023年第十四届蓝桥杯省赛中,JavaB组的个人题目被成功解决并获得了全部奖项(AK)。选手们通过展现出色的编程能力和问题解决技巧,成功完成了比赛中的各项挑战。这些解答展示了他们在Java编程领域的实力和智慧,体现了他们的努力和成果。
2023年第十四届蓝桥杯省赛JavaB组个人题解(AK)
- A: 阶乘求和
- B: 幸运数字
- C: 数组分割
- D: 矩形总面积
- E: 蜗牛
- F: 合并区域
- G: 买二赠一
- H: 合并石子
- I: 最大开支
- J: 魔法阵
之前在dotcpp上发了几个单独题解,现在补一篇完整的吧
P.S. 当天比完,一回去被室友感染甲流发烧躺了一周,。。(喜
今年相较去年,难度有提升(特别是C++),签到题不怎么签到了。脱离捞钱杯?
2023.4.27:更新 H、J;
2023.4.28:更新 F 正确题解;
2024.2.03:G题hacked,思考ing
A: 阶乘求和
本题总分:5分
【问题描述】
令 S = 1 ! + 2 ! + 3 ! + . . . + 202320232023 ! S = 1! + 2! + 3! + ... + 202320232023! S=1!+2!+3!+...+202320232023!,求 S S S 的末尾 9 位数字。 提示:答案首位不为 0。
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一 个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
420940313
大于 39 39 39后的阶乘都大于 1 e 9 1e9 1e9,遍历即可
static void solve() { ans=1; long res=1; for(int i=2;i res=res*i%(long)1e9; ans =ans+ res; ans%=(long)1e9; System.out.println(ans); } } int x = i; int mod = 0; while(x0) { mod+= x%2; x>>=1; } if(i%mod !=0) return false; x=i;mod=0; while(x>0) { mod += x%8; x/=8; } if(i%mod !=0) return false; x=i;mod=0; while(x>0) { mod += x%10; x/=10; } if(i%mod !=0) return false; x=i;mod=0; while(x>0) { mod += x%16; x/=16; } if(i%mod !=0) return false; return true; } static void solve() throws IOException{ for(int i=1,cnt=0;;i++) { if(check(i)) cnt++; if(cnt==2023) { System.out.println(i); break; } } }C: 数组分割
时间限制: 1.0 s 1.0 s 1.0s 内存限制: 512.0 M B 512.0 MB 512.0MB 本题总分: 10 10 10 分
【问题描述】
小蓝有一个长度为 N N N 的数组 A = [ A 0 , A 1 , . . . , A N − 1 ] A = [A_0, A_1,..., A_{N−1}] A=[A0,A1,...,AN−1]。现在小蓝想要从 A A A 对应的数组下标所构成的集合 I = { 0 , 1 , 2 , . . . , N − 1 } I = \{0, 1, 2, . . . , N − 1\} I={0,1,2,...,N−1} 中找出一个子集 R 1 R_1 R1,那么 R 1 R_1 R1在 I I I 中的补集为 R 2 R_2 R2。记 S 1 = ∑ r ∈ R 1 A r , S 2 = ∑ r ∈ R 2 A r S_1=∑_{r∈R_1}A_r,S_2 =∑_{r∈R2}A_r S1=∑r∈R1Ar,S2=∑r∈R2Ar,我们要求 S 1 S_1 S1 和 S 2 S_2 S2 均为偶数,请问在这种情况下共有多少种不同的 R 1 R_1 R1。当 R 1 R_1 R1 或 R 2 R_2 R2 为空集时我们将 S 1 S_1 S1 或 S 2 S_2 S2 视为 0。
【输入格式】
第一行一个整数 T T T,表示有 T T T 组数据。
接下来输入 T T T 组数据,每组数据包含两行:第一行一个整数 N N N,表示数组 A A A 的长度;第二行输入 N N N 个整数从左至右依次为 A 0 , A 1 , . . . , A N − 1 A_0, A_1, . . . , A_{N−1} A0,A1,...,AN−1,相邻元素之间用空格分隔。
【输出格式】
对于每组数据,输出一行,包含一个整数表示答案,答案可能会很大,你需要将答案对 1000000007 1000000007 1000000007 进行取模后输出。
【样例输入】
2 2 6 6 2 1 6
【样例输出】
4 0
【提示】
对于第一组数据,答案为 4 4 4。(注意:大括号内的数字表示元素在数组中的下标。)
R 1 = { 0 } , R 2 = { 1 } R_1 = \{0\}, R_2 = \{1\} R1={0},R2={1};此时 S 1 = A 0 = 6 S_1 = A_0 = 6 S1=A0=6 为偶数, S 2 = A 1 = 6 S_2 = A_1 = 6 S2=A1=6 为偶数。
R 1 = { 1 } , R 2 = { 0 } R_1 = \{1\}, R_2 = \{0\} R1={1},R2={0};此时 S 1 = A 1 = 6 S_1 = A_1 = 6 S1=A1=6 为偶数, S 2 = A 0 = 6 S_2 = A_0 = 6 S2=A0=6 为偶数。
R 1 = { 0 , 1 } , R 2 = { } R_1 = \{0, 1\}, R_2 = \{\} R1={0,1},R2={};此时 S 1 = A 0 + A 1 = 12 S_1 = A_0 + A_1 = 12 S1=A0+A1=12 为偶数, S 2 = 0 S_2 = 0 S2=0 为偶数。
R 1 = { } , R 2 = { 0 , 1 } R_1 = \{\}, R_2 = \{0, 1\} R1={},R2={0,1};此时 S 1 = 0 S_1 = 0 S1=0 为偶数, S 2 = A 0 + A 1 = 12 S_2 = A_0 + A_1 = 12 S2=A0+A1=12 为偶数。
对于第二组数据,无论怎么选择,都不满足条件,所以答案为 0。
对于 20% 的评测用例, 1 ≤ N ≤ 10 1 ≤ N ≤ 10 1≤N≤10。
对于 40% 的评测用例, 1 ≤ N ≤ 1 0 2 1 ≤ N ≤ 10^2 1≤N≤102。
对于 100% 的评测用例, 1 ≤ T ≤ 10 , 1 ≤ N ≤ 1 0 3 , 0 ≤ A i ≤ 1 0 9 1 ≤ T ≤ 10, 1 ≤ N ≤ 10^3 , 0 ≤ A_i ≤ 10^9 1≤T≤10,1≤N≤103,0≤Ai≤109。
逆元 + 组合数显然总和为奇的答案为0.
总和为偶数的,统计奇数、偶数个数为ji、ou,预处理组合数按式子计算即可.
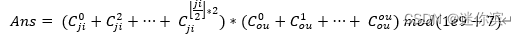
化简也是可以的。
public class Main { static int n,m,mod=(int)1e9+7,maxn=200010; static long ans=0,INF=(long)1e18; static Scanner sc = new Scanner (System.in); public static void main(String[]args) throws IOException{ int T = 1; T = sc.nextInt(); pre(); while(T-->0) solve(); } static long fac[] = new long[1002]; static long inv[] = new long[1002]; static long qpow(long a,long b) { long res = 1; a%=mod; while(b>0) { if(b%2==1) res = res*a%mod; a = a*a%mod; b/=2; } return res; } static void pre() { fac[0] = inv[0] =1; for(int i=1;i fac[i] = fac[i-1]*i%mod; inv[i] = qpow(fac[i],mod-2); } } static void solve() throws IOException{ n = sc.nextInt(); int a[] = new int [n+1]; int ji=0,ou=0, sum=0; for(int i=1;i a[i] = sc.nextInt()%2; if(a[i]%2==0) ou++; else ji++; sum+=a[i]; } if(sum%2==1) { System.out.println(0);return; } ans = 0; for(int i=0;i static int maxn = 200005,n,m; static long INF = (long)2e18,ans = 0,mod = (int)1e9+7; static Scanner sc = new Scanner (System.in); public static void main(String[]args) throws IOException{ int T = 1; while(T--0) solve(); pw.flush(); } static long x1,x2,x3,x4,y1,y2,y3,y4; static boolean check1() { // 四角 if(x3 ans -= (Math.min(x2, x4)-x3) *(Math.min(y4, y2)-y3); return true; } if(x4 = x1 && x4 ans -= (x4 - Math.max(x1, x3)) *(Math.min(y4, y2)-y3); return true; } if(x4 = x1 && x4 ans -= (x4 - Math.max(x1, x3)) *(y4 - Math.max(y1, y3)); return true; } if(x3 = x1 && x3 ans -= (Math.min(x2, x4)-x3) *(y4 - Math.max(y1, y3)); return true; } return false; } static void check2() { //四角都不重合在矩形内部 if(x1 x1=sc.nextInt();y1=sc.nextInt();x2=sc.nextInt();y2=sc.nextInt(); x3=sc.nextInt();y3=sc.nextInt();x4=sc.nextInt();y4=sc.nextInt(); ans = (x2-x1)*(y2-y1) + (x4-x3) *(y4-y3); if(check1()) pw.println(ans); else { long t; t=x1;x1=x3;x3=t; t=x2;x2=x4;x4=t; t=y1;y1=y3;y3=t; t=y2;y2=y4;y4=t; if(check1()) pw.println(ans); else { check2(); pw.println(ans); } } } } static int maxn = 200005,n,m; static long INF = (long)2e18,ans = 0,mod = (int)1e9+7; static Scanner sc = new Scanner (System.in); static PrintWriter pw = new PrintWriter(new OutputStreamWriter(System.out)); public static void main(String[]args) throws IOException{ int T = 1; //T = Integer.parseInt(S()); while(T--0) solve(); pw.flush(); } static final int I() throws IOException { st.nextToken(); return (int)st.nval; } static void solve() throws IOException{ n = sc.nextInt(); long x[] = new long [n+1]; for(int i=1;i a[i] = sc.nextInt();;b[i] = sc.nextInt(); } double dp[][] = new double[n+1][2]; dp[1][0] = x[1]; //底端最小用时 dp[1][1] = x[1] + a[1] / 0.7; //传送门用时 for(int i=2; i dp[i][0] = Math.min(dp[i-1][0]+x[i]-x[i-1], dp[i-1][1] + b[i-1]/1.3); dp[i][1] = Math.min(dp[i][0] + a[i] / 0.7, dp[i-1][1] + ((b[i-1]a[i])?(b[i-1]-a[i])/1.3: (a[i]-b[i-1])/0.7)); } pw.printf("%.2f",dp[n][0]); } } static int maxn = 200005,n,m; static long INF = (long)2e18,ans = 0,mod = (int)1e9+7; static Scanner sc = new Scanner (System.in); static BufferedReader bf = new BufferedReader(new InputStreamReader(System.in)); static StreamTokenizer st =new StreamTokenizer(bf); static PrintWriter pw = new PrintWriter(new OutputStreamWriter(System.out)); public static void main(String[]args) throws IOException{ int T = 1; while(T--0) solve(); pw.flush(); } static final int I() throws IOException { st.nextToken(); return (int)st.nval; } static int [][]g = new int [500][500]; static int w[][] = new int [55][55]; static boolean f[][] = new boolean [500][500]; static int x1,x2,y1,y2; static void clear(int a,int b) { for(int i=a;i if(op == 0) { for(int i=a;i //逆时针1次 for(int j = b,u = 0 ; j //顺时针1次 for(int j = b+n-1,u = 0 ; j=b ; j--,u++) for(int i = a,v=0 ; i //倒置 for(int i = a+n-1,u = 0 ; i =a ; i--,u++) for(int j = b+n-1,v=0 ; j=b ; j--,v++) g[i][j] = w[u][v]; } } static void ppp() { System.out.println("graph:"); for(int i=x1;i for(int j=y1;j System.out.print(g[i][j]+" "); } System.out.println(); } } static int x[] = {1,-1,0,0}; static int y[] = {0,0,1,-1}; static int bfs(int aa,int bb) { Queue int k = q.poll(); int a = k/1000,b=k%1000; if(f[a][b]) continue; res++; f[a][b]=true; for(int i=0;i int xx = a+x[i],yy = y[i]+b; if(xx=x1 && xx int res = 0; for(int u = x1 ; u res = Math.max(res, bfs(u,v)); } m=res; ans = Math.max(ans, res); } static void solve() throws IOException{ n = I(); for(int i = 60 ; i //上 for(int j=0;j add(60-n,i,j); x1 =60-n;y1 = Math.min(60, i); x2 = 60+n-1; y2 = Math.max(60+n-1, i+n-1); //ppp(); work(); //System.out.println(m); clear(60-n,i); } } for(int i = 60-n+1 ; i //下 for(int j=0;j add(60+n,i,j); x1 =60;y1 = Math.min(60, i); x2 = 60+2*n-1; y2 = Math.max(60+n-1, i+n-1); //ppp(); work(); //System.out.println(m); clear(60+n,i); } } for(int i = 60-n+1 ; i //左 for(int j=0;j add(i,60-n,j); x1 =Math.min(i, 60);y1 = 60-n; x2 = Math.max(i+n-1, 60+n-1); y2 = 60+n-1; //ppp(); work(); //System.out.println(m); clear(i,60-n); } } for(int i = 60-n+1 ; i //右 for(int j=0;j add(i,60+n,j); x1 =Math.min(i, 60);y1 = 60; x2 = Math.max(i+n-1, 60+n-1); y2 = 60+2*n-1; //ppp(); work(); //System.out.println(m); clear(i,60+n); } } pw.println(ans); } } static int n,m,mod=(int)1e9+7,maxn=500010; static long ans=0,INF=(long)1e18; static Scanner sc = new Scanner (System.in); static BufferedReader bf = new BufferedReader(new InputStreamReader(System.in)); static StreamTokenizer st = new StreamTokenizer(bf); static PrintWriter pw = new PrintWriter(System.out); public static void main(String[]args) throws IOException{ int T = 1; //T = I(); while(T--0) solve(); pw.flush(); } static int I() throws IOException{ st.nextToken(); return (int)st.nval; } static int a[] = new int [maxn]; static boolean f[] = new boolean [maxn]; static int find(int x) { int l=1,r=n; int res =0; while(l int mid = (l+r)/2; if(f[mid]) { //先前赠送过,跳到左边 r=mid-1;continue; } if(a[mid] res = Math.max(res, mid); l = mid+1; } else r = mid-1; } return res; } static void solve() throws IOException{ n = I(); for(int i=1 ;i if(f[i]) continue;//赠送过,跳过 ans += a[i]; t++; if(t == 2) { t=0; int id = find(a[i]/2); if(id0) f[id]=true; } } pw.println(ans); } } static int maxn = 200005,n,m,inf=(int)1e9; static long INF = (long)2e18,ans = 0,mod = (int)1e9+7; static Scanner sc = new Scanner (System.in); static BufferedReader bf = new BufferedReader(new InputStreamReader(System.in)); static StreamTokenizer st =new StreamTokenizer(bf); static PrintWriter pw = new PrintWriter(new OutputStreamWriter(System.out)); public static void main(String[]args) throws IOException{ int T = 1; while(T--0) solve(); pw.flush(); } static final int I() throws IOException { st.nextToken(); return (int)st.nval; } static int dp[][][] = new int [303][303][3]; static int num[][] = new int [303][303]; static int a[] = new int [301]; static int sum[] = new int [301]; //前缀和 static int c[] = new int [301]; static int cost[][] = new int [303][303]; static void solve() throws IOException{ n= I(); for(int i=1;i num[i][j]=j-i+1; for(int k=0;k a[i] = I(); sum[i]=a[i]+sum[i-1]; //前缀和,方便统计区间 } for(int i=1;i c[i] = I();//颜色 dp[i][i][c[i]] = 0; //初始石子堆花费显然为0 } for(int len=1;len int j=i+len-1; for(int col=0;col int min = inf; for(int k=i;k if(dp[i][k][col]!=inf && dp[k+1][j][col]!=inf) { min = Math.min(min, dp[i][k][col] + dp[k+1][j][col]); } } if(min==inf) continue; num[i][j]=1; dp[i][j][(col+1)%3] = Math.min(dp[i][j][(col+1)%3], min+sum[j]-sum[i-1]); cost[i][j] = Math.min(dp[i][j][0], Math.min(dp[i][j][1], dp[i][j][2])); } } for(int k=1;k if(num[i][j] num[i][k] + num[k+1][j]) { num[i][j] = num[i][k] + num[k+1][j]; cost[i][j] = cost[i][k]+cost[k+1][j]; } else if(num[i][j] == num[i][k] + num[k+1][j]) { cost[i][j] = Math.min(cost[i][j], cost[i][k]+cost[k+1][j]); } } pw.println(num[1][n]+" "+cost[1][n]); } } static int maxn = 200005,n,m; static long INF = (long)2e18,ans = 0,mod = (int)1e9+7; static Scanner sc = new Scanner (System.in); static BufferedReader bf = new BufferedReader(new InputStreamReader(System.in)); static StreamTokenizer st =new StreamTokenizer(bf); static PrintWriter pw = new PrintWriter(new OutputStreamWriter(System.out)); public static void main(String[]args) throws IOException{ int T = 1; while(T--0) solve(); pw.flush(); } static final int I() throws IOException { st.nextToken(); return (int)st.nval; } static class node implements Comparable long k=0,b=0; int num=0; public node(long a,long bb) { k=a;b=bb; } @Override public int compareTo(node o) { // TODO Auto-generated method stub long x = (this.num+1)*Math.max(0, k*(num+1)+b) - num*Math.max(0, k*num+b); long y = (o.num+1)*Math.max(0, o.k*(o.num+1)+o.b) - o.num*Math.max(0, o.k*o.num+o.b); return x n=I(); m=I(); PriorityQueue long k=I(),b=I(); q.add(new node(k,b)); } while(n--0) { node o = q.poll(); if((o.num+1)*Math.max(0, o.k*(o.num+1)+o.b) - o.num*Math.max(0, o.k*o.num+o.b) q.add(o);break; } o.num++; q.add(o); } while(!q.isEmpty()) { node o = q.poll(); ans += o.num*Math.max(0, o.k*o.num+o.b); } pw.println(ans); } } static int maxn = 200005,n,m,inf=(int)1e9; static long INF = (long)2e18,ans = 0,mod = (int)1e9+7; static Scanner sc = new Scanner (System.in); static BufferedReader bf = new BufferedReader(new InputStreamReader(System.in)); static StreamTokenizer st =new StreamTokenizer(bf); static PrintWriter pw = new PrintWriter(new OutputStreamWriter(System.out)); public static void main(String[]args) throws IOException{ int T = 1; while(T--0) solve(); pw.flush(); } static final int I() throws IOException { st.nextToken(); return (int)st.nval; } static class node{ int to; int w; public node(int a,int b) { to=a;w=b; } } static Vector for(int i=0;i0,0}); while(!q.isEmpty()) { int []p = q.poll(); int x=p[0],j=p[1]; for(node o:g.get(x)) { int y = o.to,w = o.w; if(j if(d[y][j+1] d[x][j]){ d[y][j+1] = d[x][j]; q.add(new int[]{y,j+1}); } } if(j==0||j==k){ if(d[y][j] d[x][j]+w){ d[y][j] = d[x][j]+w; q.add(new int[]{y,j}); } } } } } static void solve() throws IOException{ n=I();k=I();m=I(); for(int i=0;i int u=I(),v=I(),w=I(); g.get(u).add(new node(v,w)); g.get(v).add(new node(u,w)); } dij(); pw.println(Math.min(d[n-1][0], d[n-1][k])); } }






还没有评论,来说两句吧...