华为OD机试 - 生成哈夫曼树（Java & JS & Python & C & C++），华为OD机试，生成哈夫曼树（多语言实现）

摘要：华为OD机试中涉及生成哈夫曼树的编程任务，可使用Java、JavaScript、Python、C和C++等语言实现。哈夫曼树是一种应用广泛的数据结构，用于数据压缩和编码等领域。该任务要求根据给定的数据构建哈夫曼树，并熟练掌握相应编程语言的语法和算法设计，以完成高效的编码和解码过程。

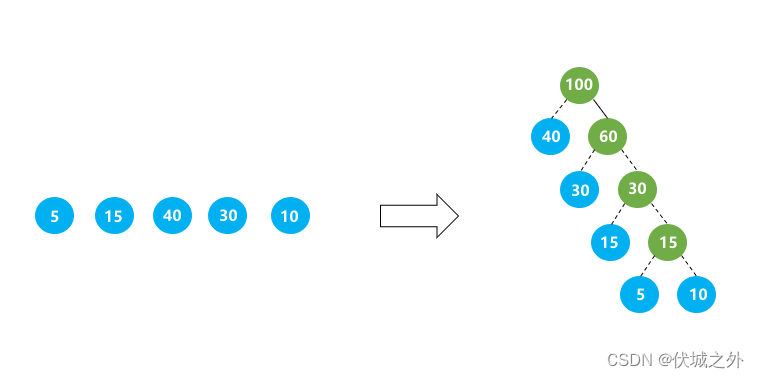
给定一个无序的数字数组，每个数字代表二叉树的叶子节点的权值，数字数组的值均大于等于1，我们需要根据这个数组生成哈夫曼树，并按照中序遍历输出，为了保证输出的二叉树中序遍历结果统一，我们设定了以下规则：在二叉树节点中，左节点的权值小于右节点的权值，根节点的权值为左右节点权值之和，当左右节点权值相同时，左子树的高度小于等于右子树的高度。

需要注意的是，所有用例都是有效的，并能生成哈夫曼树。

哈夫曼树是一种带权路径长度最短的二叉树，也称为最优二叉树，树的带权路径长度是指树中所有叶节点的权值乘上其到根节点的路径长度（若根节点为0层，叶节点到根节点的路径长度为叶节点的层数）。

输入描述

对于给定的叶子节点权值数组，5，15，40，30，10，生成的最优二叉树如上所示，该树的最短带权路径长度为：40 * 1 + 30 * 2 + 15 * 3 + 5 * 4 + 10 * 4 = 205。

算法描述

为了解决这个问题，我们可以按照以下步骤进行：

1、构建哈夫曼树：根据给定的叶子节点权值数组，使用哈夫曼算法构建哈夫曼树，哈夫曼算法的基本思想是根据权值大小构建二叉树，使得带权路径长度最短。

2、中序遍历：对构建好的哈夫曼树进行中序遍历，输出遍历结果，中序遍历的顺序是左子树-根节点-右子树。

3、保证节点权值和高度规则：在构建哈夫曼树的过程中，确保左节点的权值小于右节点的权值，并在必要时调整子树的高度以满足限制条件。

通过以上步骤，我们可以根据给定的叶子节点权值数组生成符合要求的哈夫曼树，并按中序遍历输出。