【C++】AVL树，C++中的AVL树实现与原理，C++中AVL树的实现原理及实践指南，C++中AVL树的实现原理与实践指南，从理论到实践详解，C++中AVL树的实现原理与实践，从理论到实践的详解指南，C++中AVL树的实现原理与实践，从理论到实践的详细指南

摘要：本指南介绍了C++中的AVL树实现与原理，从理论到实践全面解析AVL树的实现方式。内容包括AVL树的基本概念、实现原理、实践指南，以及从理论到实践的详细步骤和解析。通过阅读本指南，读者能够深入了解AVL树的原理，并学会在C++中实践应用，提高数据结构和算法方面的技能。

本文将详细介绍C++中的AVL树实现及其工作原理，通过清晰易懂的解释，本文将全面涵盖AVL树的实现原理，包括平衡条件的判断、节点的旋转操作等，本文还将提供实践指南，从理论到实践全面讲解AVL树的实现过程，以帮助读者更好地理解和应用AVL树。

定义节点结构：

在C++中，AVL树的节点结构包括键值、高度以及指向左右子节点和父节点的指针，节点结构的定义如下：

template <typename K>
struct AVLNode {
    K key;                   // 节点的键值
    int height;              // 节点的高度
    AVLNode* left;           // 左子节点指针
    AVLNode* right;          // 右子节点指针
    AVLNode* parent;         // 指向父节点的指针（可选，根据实际需求决定是否包含）
};

定义AVL树类：

AVL树类包含构造函数、插入节点、删除节点等成员函数，还包括根节点指针、获取节点高度和平衡节点的辅助函数，类的定义如下：

template <typename K>
class AVLTree {
public:
    AVLTree();                          // 构造函数
    bool Insert(const K& key);          // 插入节点
    bool Delete(const K& key);          // 删除节点
    // 其他成员函数，如查找、遍历等
private:
    AVLNode<K>* root;                  // 根节点指针
    int GetHeight(AVLNode<K>* node);   // 获取节点高度辅助函数
    AVLNode<K>* Balance(AVLNode<K>* node, bool isLeftChild); // 平衡节点辅助函数
    void RotateLeft(AVLNode<K>*& node); // 左旋转操作
    void RotateRight(AVLNode<K>*& node); // 右旋转操作
};

实现节点的插入操作：

插入节点时，首先进行二叉搜索树的插入操作，接着检查节点的平衡因子，如果插入导致不平衡，则进行相应的旋转操作，旋转操作分为左旋转和右旋转，用于处理左右子树高度不平衡的情况，插入操作的流程可以通过图示来详细说明，以便更好地理解。

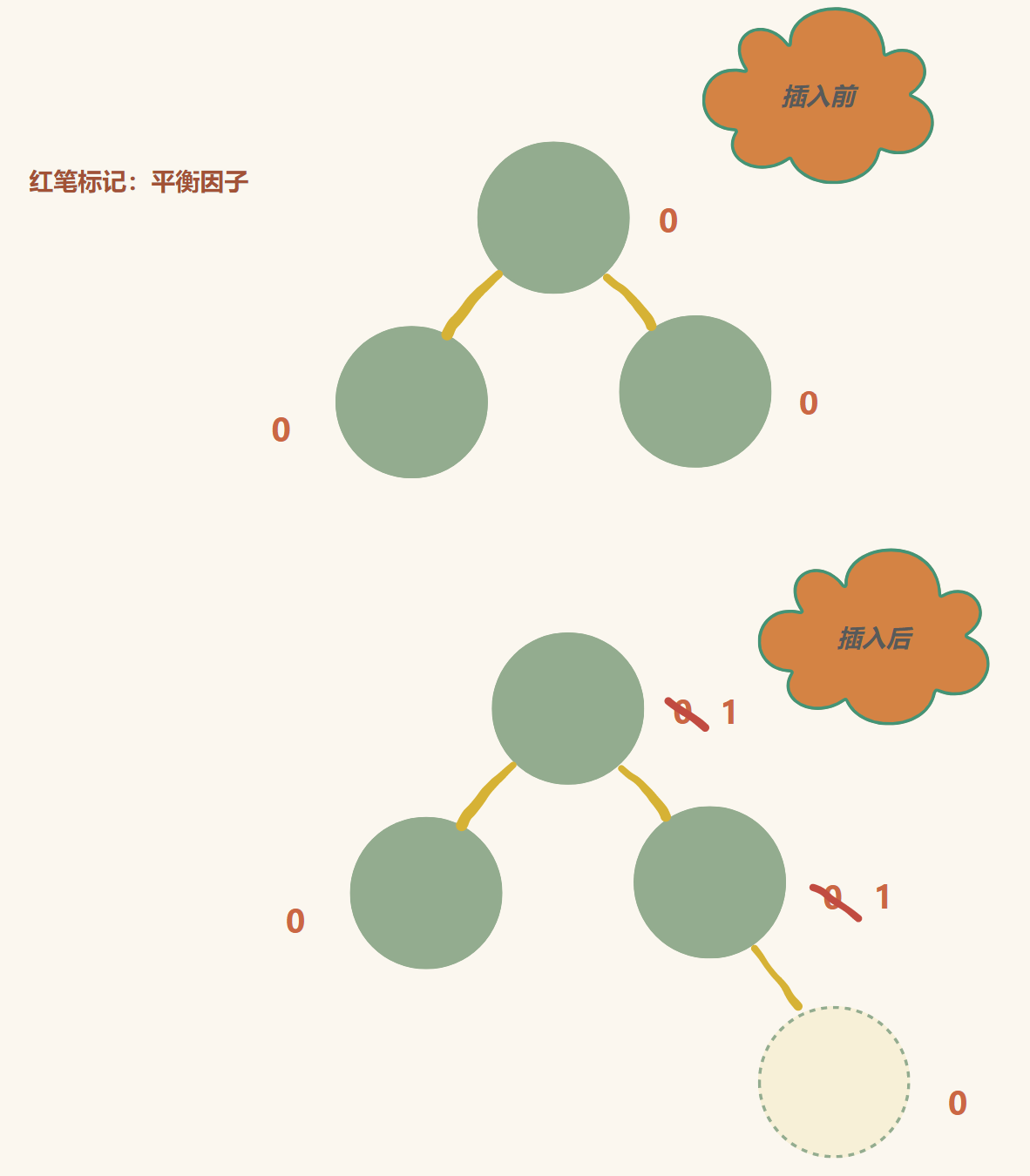
实现节点的删除操作：

删除节点时，首先进行二叉搜索树的删除操作，然后检查删除后的节点的平衡因子，如果删除导致不平衡，进行相应的旋转操作，注意处理删除操作可能导致的兄弟节点平衡因子变化，删除操作的流程同样可以辅以图示说明，在删除操作中，可以使用异常处理机制来处理异常情况并给出错误信息。

异常处理：

当插入和删除操作中遇到无法修复的不平衡情况时，可以使用异常处理机制来报告错误或抛出异常，可以自定义一个异常类来处理异常情况，并提供相应的错误信息。

其他功能实现与优化：

除了插入和删除操作，AVL树还可以提供查找、遍历等功能，这些功能可以根据实际需求进行实现和优化，在实际应用中，还可以考虑添加其他辅助函数和成员变量来提高效率和方便使用，添加获取树的高度、获取节点的父节点等辅助函数，为了提高代码的可读性和可维护性，应添加必要的注释和文档说明，使用代码格式化工具使代码整洁易读也是很好的实践。

希望这些补充和修饰可以帮助你进一步完善文章。