温馨提示:这篇文章已超过445天没有更新,请注意相关的内容是否还可用!
摘要:针对Android工程师面试,字节力扣刷题需有针对性。常见数据结构与算法面试题合集出炉,涵盖各种题型,帮助工程师提高算法能力,针对性准备面试。通过刷题和复习,提高面试通过率,更好地掌握面试技巧。
return null;
}
Node nodeResult = null;
Node nodePre = null;
Node current = head;
while (current != null) {
Node nodeNext = current.next;
if (nodeNext == null) {
nodeResult = current;
}
current.next = nodePre;
nodePre = current;
current = nodeNext;
}
return nodeResult;
}
上面的几段代码主要展示了链表的几个基本操作,还有很多像获取指定元素,移除元素等操作大家可以自己完成,写这些代码的时候一定要理清节点之间关系,这样才不容易出错。
链表的实现还有其它的方式,常见的有循环单链表,双向链表,循环双向链表。 循环单链表 主要是链表的最后一个节点指向第一个节点,整体构成一个链环。 双向链表 主要是节点中包含两个指针部分,一个指向前驱元,一个指向后继元,JDK中LinkedList集合类的实现就是双向链表。** 循环双向链表** 是最后一个节点指向第一个节点。
二、栈与队列
栈和队列也是比较常见的数据结构,它们是比较特殊的线性表,因为对于栈来说,访问、插入和删除元素只能在栈顶进行,对于队列来说,元素只能从队列尾插入,从队列头访问和删除。
栈
栈是限制插入和删除只能在一个位置上进行的表,该位置是表的末端,叫作栈顶,对栈的基本操作有push(进栈)和pop(出栈),前者相当于插入,后者相当于删除最后一个元素。栈有时又叫作LIFO(Last In First Out)表,即后进先出。

下面我们看一道经典题目,加深对栈的理解。

上图中的答案是C,其中的原理可以好好想一想。
因为栈也是一个表,所以任何实现表的方法都能实现栈。我们打开JDK中的类Stack的源码,可以看到它就是继承类Vector的。当然,Stack是Java2前的容器类,现在我们可以使用LinkedList来进行栈的所有操作。
队列
队列是一种特殊的线性表,特殊之处在于它只允许在表的前端(front)进行删除操作,而在表的后端(rear)进行插入操作,和栈一样,队列是一种操作受限制的线性表。进行插入操作的端称为队尾,进行删除操作的端称为队头。

我们可以使用链表来实现队列,下面代码简单展示了利用LinkedList来实现队列类。
- 代码9 简单实现队列类
public class MyQueue {
private LinkedList list = new LinkedList();
// 入队
public void enqueue(E e) {
list.addLast(e);
}
// 出队
public E dequeue() {
return list.removeFirst();
}
}
普通的队列是一种先进先出的数据结构,而优先队列中,元素都被赋予优先级。当访问元素的时候,具有最高优先级的元素最先被删除。优先队列在生活中的应用还是比较多的,比如医院的急症室为病人赋予优先级,具有最高优先级的病人最先得到治疗。在Java集合框架中,类PriorityQueue就是优先队列的实现类,具体大家可以去阅读源码。
三、树与二叉树
树型结构是一类非常重要的非线性数据结构,其中以树和二叉树最为常用。在介绍二叉树之前,我们先简单了解一下树的相关内容。
树
** 树 是由n(n>=1)个有限节点组成一个具有层次关系的集合。它具有以下特点:每个节点有零个或多个子节点;没有父节点的节点称为 根 节点;每一个非根节点有且只有一个 父节点 **;除了根节点外,每个子节点可以分为多个不相交的子树。

二叉树基本概念
- 定义
二叉树是每个节点最多有两棵子树的树结构。通常子树被称作“左子树”和“右子树”。二叉树常被用于实现二叉查找树和二叉堆。
- 相关性质
二叉树的每个结点至多只有2棵子树(不存在度大于2的结点),二叉树的子树有左右之分,次序不能颠倒。
二叉树的第i层至多有2(i-1)个结点;深度为k的二叉树至多有2k-1个结点。
一棵深度为k,且有2^k-1个节点的二叉树称之为** 满二叉树 **;
深度为k,有n个节点的二叉树,当且仅当其每一个节点都与深度为k的满二叉树中,序号为1至n的节点对应时,称之为** 完全二叉树 **。

- 三种遍历方法
在二叉树的一些应用中,常常要求在树中查找具有某种特征的节点,或者对树中全部节点进行某种处理,这就涉及到二叉树的遍历。二叉树主要是由3个基本单元组成,根节点、左子树和右子树。如果限定先左后右,那么根据这三个部分遍历的顺序不同,可以分为先序遍历、中序遍历和后续遍历三种。
(1) 先序遍历 若二叉树为空,则空操作,否则先访问根节点,再先序遍历左子树,最后先序遍历右子树。 (2) 中序遍历 若二叉树为空,则空操作,否则先中序遍历左子树,再访问根节点,最后中序遍历右子树。(3) 后序遍历 若二叉树为空,则空操作,否则先后序遍历左子树访问根节点,再后序遍历右子树,最后访问根节点。

- 树和二叉树的区别
(1) 二叉树每个节点最多有2个子节点,树则无限制。 (2) 二叉树中节点的子树分为左子树和右子树,即使某节点只有一棵子树,也要指明该子树是左子树还是右子树,即二叉树是有序的。 (3) 树决不能为空,它至少有一个节点,而一棵二叉树可以是空的。
上面我们主要对二叉树的相关概念进行了介绍,下面我们将从二叉查找树开始,介绍二叉树的几种常见类型,同时将之前的理论部分用代码实现出来。
二叉查找树
- 定义
二叉查找树就是二叉排序树,也叫二叉搜索树。二叉查找树或者是一棵空树,或者是具有下列性质的二叉树: (1) 若左子树不空,则左子树上所有结点的值均小于它的根结点的值;(2) 若右子树不空,则右子树上所有结点的值均大于它的根结点的值;(3) 左、右子树也分别为二叉排序树;(4) 没有键值相等的结点。
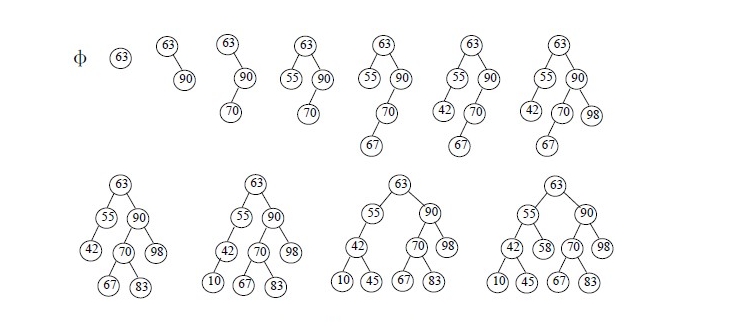
- 性能分析
对于二叉查找树来说,当给定值相同但顺序不同时,所构建的二叉查找树形态是不同的,下面看一个例子。
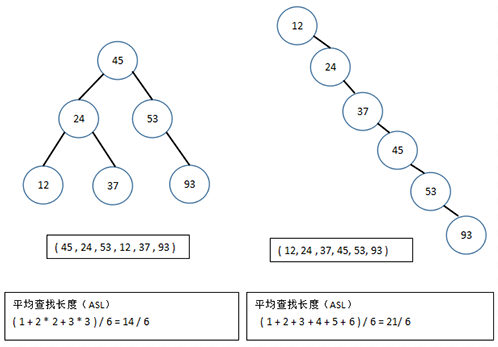
可以看到,含有n个节点的二叉查找树的平均查找长度和树的形态有关。最坏情况下,当先后插入的关键字有序时,构成的二叉查找树蜕变为单支树,树的深度为n,其平均查找长度(n+1)/2(和顺序查找相同),最好的情况是二叉查找树的形态和折半查找的判定树相同,其平均查找长度和log2(n)成正比。平均情况下,二叉查找树的平均查找长度和logn是等数量级的,所以为了获得更好的性能,通常在二叉查找树的构建过程需要进行“平衡化处理”,之后我们将介绍平衡二叉树和红黑树,这些均可以使查找树的高度为O(log(n))。
- 代码10 二叉树的节点
class TreeNode {
E element;
TreeNode left;
TreeNode right;
public TreeNode(E e) {
element = e;
}
}
二叉查找树的三种遍历都可以直接用递归的方法来实现:
- 代码12 先序遍历
protected void preorder(TreeNode root) {
if (root == null)
return;
System.out.println(root.element + " ");
preorder(root.left);
preorder(root.right);
}
- 代码13 中序遍历
protected void inorder(TreeNode root) {
if (root == null)
return;
inorder(root.left);
System.out.println(root.element + " ");
inorder(root.right);
}
- 代码14 后序遍历
protected void postorder(TreeNode root) {
if (root == null)
return;
postorder(root.left);
postorder(root.right);
System.out.println(root.element + " ");
}
- 代码15 二叉查找树的简单实现
/**
- @author JackalTsc
*/
public class MyBinSearchTree {
// 根
private TreeNode root;
// 默认构造函数
public MyBinSearchTree() {
}
// 二叉查找树的搜索
public boolean search(E e) {
TreeNode current = root;
while (current != null) {
if (e.compareTo(current.element)
current = current.left;
} else if (e.compareTo(current.element) > 0) {
current = current.right;
} else {
return true;
}
}
return false;
}
// 二叉查找树的插入
public boolean insert(E e) {
// 如果之前是空二叉树 插入的元素就作为根节点
if (root == null) {
root = createNewNode(e);
} else {
// 否则就从根节点开始遍历 直到找到合适的父节点
TreeNode parent = null;
TreeNode current = root;
while (current != null) {
if (e.compareTo(current.element)
parent = current;
current = current.left;
} else if (e.compareTo(current.element) > 0) {
parent = current;
current = current.right;
} else {
return false;
}
}
// 插入
if (e.compareTo(parent.element)
parent.left = createNewNode(e);
} else {
parent.right = createNewNode(e);
}
}
return true;
}
// 创建新的节点
protected TreeNode createNewNode(E e) {
return new TreeNode(e);
}
}
// 二叉树的节点
class TreeNode {
E element;
TreeNode left;
TreeNode right;
public TreeNode(E e) {
element = e;
}
}
上面的代码15主要展示了一个自己实现的简单的二叉查找树,其中包括了几个常见的操作,当然更多的操作还是需要大家自己去完成。因为在二叉查找树中删除节点的操作比较复杂,所以下面我详细介绍一下这里。
- 二叉查找树中删除节点分析
要在二叉查找树中删除一个元素,首先需要定位包含该元素的节点,以及它的父节点。假设current指向二叉查找树中包含该元素的节点,而parent指向current节点的父节点,current节点可能是parent节点的左孩子,也可能是右孩子。这里需要考虑两种情况:
current节点没有左孩子,那么只需要将patent节点和current节点的右孩子相连。
current节点有一个左孩子,假设rightMost指向包含current节点的左子树中最大元素的节点,而parentOfRightMost指向rightMost节点的父节点。那么先使用rightMost节点中的元素值替换current节点中的元素值,将parentOfRightMost节点和rightMost节点的左孩子相连,然后删除rightMost节点。
// 二叉搜索树删除节点
public boolean delete(E e) {
TreeNode parent = null;
TreeNode current = root;
// 找到要删除的节点的位置
while (current != null) {
if (e.compareTo(current.element)
parent = current;
current = current.left;
} else if (e.compareTo(current.element) > 0) {
parent = current;
current = current.right;
} else {
break;
}
}
// 没找到要删除的节点
if (current == null) {
return false;
}
// 考虑第一种情况
if (current.left == null) {
if (parent == null) {
root = current.right;
} else {
if (e.compareTo(parent.element)
parent.left = current.right;
} else {
parent.right = current.right;
}
}
} else { // 考虑第二种情况
TreeNode parentOfRightMost = current;
TreeNode rightMost = current.left;
// 找到左子树中最大的元素节点
while (rightMost.right != null) {
parentOfRightMost = rightMost;
rightMost = rightMost.right;
}
// 替换
current.element = rightMost.element;
// parentOfRightMost和rightMost左孩子相连
if (parentOfRightMost.right == rightMost) {
parentOfRightMost.right = rightMost.left;
} else {
parentOfRightMost.left = rightMost.left;
}
}
return true;
}
平衡二叉树
平衡二叉树又称AVL树,它或者是一棵空树,或者是具有下列性质的二叉树:它的左子树和右子树都是平衡二叉树,且左子树和右子树的深度之差的绝对值不超过1。
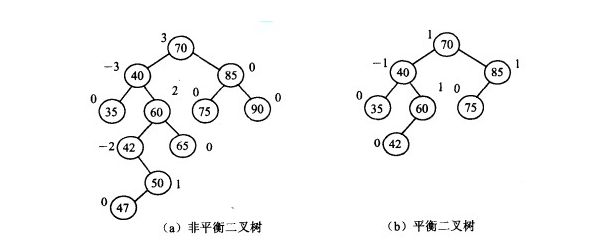
AVL树是最先发明的自平衡二叉查找树算法。在AVL中任何节点的两个儿子子树的高度最大差别为1,所以它也被称为高度平衡树,n个结点的AVL树最大深度约1.44log2n。查找、插入和删除在平均和最坏情况下都是O(log n)。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。
红黑树
红黑树是平衡二叉树的一种,它保证在最坏情况下基本动态集合操作的事件复杂度为O(log n)。红黑树和平衡二叉树区别如下:
(1) 红黑树放弃了追求完全平衡,追求大致平衡,在与平衡二叉树的时间复杂度相差不大的情况下,保证每次插入最多只需要三次旋转就能达到平衡,实现起来也更为简单。
(2) 平衡二叉树追求绝对平衡,条件比较苛刻,实现起来比较麻烦,每次插入新节点之后需要旋转的次数不能预知。
四、图
- 简介
图是一种较线性表和树更为复杂的数据结构,在线性表中,数据元素之间仅有线性关系,在树形结构中,数据元素之间有着明显的层次关系,而在图形结构中,节点之间的关系可以是任意的,图中任意两个数据元素之间都可能相关。图的应用相当广泛,特别是近年来的迅速发展,已经渗入到诸如语言学、逻辑学、物理、化学、电讯工程、计算机科学以及数学的其他分支中。
- 相关阅读
因为图这部分的内容还是比较多的,这里就不详细介绍了,有需要的可以自己搜索相关资料。
(1) 《百度百科对图的介绍》
(2) 《数据结构之图(存储结构、遍历)》
五、总结
到这里,关于常见的数据结构的整理就结束了,断断续续大概花了两天时间写完,在总结的过程中,通过查阅相关资料,结合书本内容,收获还是很大的。
数据结构与算法面试题合集
除了算法我还给大家整理了Android相关详细的面试复习资源:
接下来给大家提供一个方向,进行体系化的学习:
1、看视频进行系统学习
前几年的Crud经历,让我明白自己真的算是菜鸡中的战斗机,也正因为Crud,导致自己技术比较零散,也不够深入不够系统,所以重新进行学习是很有必要的。我差的是系统知识,差的结构框架和思路,所以通过视频来学习,效果更好,也更全面。关于视频学习,个人可以推荐去B站进行学习,B站上有很多学习视频,唯一的缺点就是免费的容易过时。
另外,我自己也珍藏了好几套视频,有需要的我也可以分享给你。
2、进行系统梳理知识,提升储备
客户端开发的知识点就那么多,面试问来问去还是那么点东西。所以面试没有其他的诀窍,只看你对这些知识点准备的充分程度。so,出去面试时先看看自己复习到了哪个阶段就好。
系统学习方向:
**架构师筑基必备技能:**深入Java泛型+注解深入浅出+并发编程+数据传输与序列化+Java虚拟机原理+反射与类加载+动态代理+高效IO
**Android高级UI与FrameWork源码:**高级UI晋升+Framework内核解析+Android组件内核+数据持久化
**360°全方面性能调优:**设计思想与代码质量优化+程序性能优化+开发效率优化
**解读开源框架设计思想:**热修复设计+插件化框架解读+组件化框架设计+图片加载框架+网络访问框架设计+RXJava响应式编程框架设计+IOC架构设计+Android架构组件Jetpack
最后
简历首选内推方式,速度快,效率高啊!然后可以在拉钩,boss,脉脉,大街上看看。简历上写道熟悉什么技术就一定要去熟悉它,不然被问到不会很尴尬!做过什么项目,即使项目体量不大,但也一定要熟悉实现原理!不是你负责的部分,也可以看看同事是怎么实现的,换你来做你会怎么做?做过什么,会什么是广度问题,取决于项目内容。但做过什么,达到怎样一个境界,这是深度问题,和个人学习能力和解决问题的态度有关了。大公司看深度,小公司看广度。大公司面试你会的,小公司面试他们用到的你会不会,也就是岗位匹配度。
面试过程一定要有礼貌!即使你觉得面试官不尊重你,经常打断你的讲解,或者你觉得他不如你,问的问题缺乏专业水平,你也一定要尊重他,谁叫现在是他选择你,等你拿到offer后就是你选择他了。
另外,描述问题一定要慢!不要一下子讲一大堆,慢显得你沉稳、自信,而且你还有时间反应思路接下来怎么讲更好。现在开发过多依赖ide,所以会有个弊端,当我们在面试讲解很容易不知道某个方法怎么读,这是一个硬伤…所以一定要对常见的关键性的类名、方法名、关键字读准,有些面试官不耐烦会说“你到底说的是哪个?”这时我们会容易乱了阵脚。正确的发音+沉稳的描述+好听的嗓音决对是一个加分项!
最重要的是心态!心态!心态!重要事情说三遍!面试时间很短,在短时间内对方要摸清你的底子还是比较不现实的,所以,有时也是看眼缘,这还是个看脸的时代。
希望大家都能找到合适自己满意的工作!
进阶学习视频

附上:我们之前因为秋招收集的二十套一二线互联网公司Android面试真题 (含BAT、小米、华为、美团、滴滴)和我自己整理Android复习笔记(包含Android基础知识点、Android扩展知识点、Android源码解析、设计模式汇总、Gradle知识点、常见算法题汇总。)

《Android学习笔记总结+移动架构视频+大厂面试真题+项目实战源码》,点击传送门,即可获取!
你来做你会怎么做?做过什么,会什么是广度问题,取决于项目内容。但做过什么,达到怎样一个境界,这是深度问题,和个人学习能力和解决问题的态度有关了。大公司看深度,小公司看广度。大公司面试你会的,小公司面试他们用到的你会不会,也就是岗位匹配度。
面试过程一定要有礼貌!即使你觉得面试官不尊重你,经常打断你的讲解,或者你觉得他不如你,问的问题缺乏专业水平,你也一定要尊重他,谁叫现在是他选择你,等你拿到offer后就是你选择他了。
另外,描述问题一定要慢!不要一下子讲一大堆,慢显得你沉稳、自信,而且你还有时间反应思路接下来怎么讲更好。现在开发过多依赖ide,所以会有个弊端,当我们在面试讲解很容易不知道某个方法怎么读,这是一个硬伤…所以一定要对常见的关键性的类名、方法名、关键字读准,有些面试官不耐烦会说“你到底说的是哪个?”这时我们会容易乱了阵脚。正确的发音+沉稳的描述+好听的嗓音决对是一个加分项!
最重要的是心态!心态!心态!重要事情说三遍!面试时间很短,在短时间内对方要摸清你的底子还是比较不现实的,所以,有时也是看眼缘,这还是个看脸的时代。
希望大家都能找到合适自己满意的工作!
进阶学习视频
[外链图片转存中…(img-huynrFAc-1714506906520)]
附上:我们之前因为秋招收集的二十套一二线互联网公司Android面试真题 (含BAT、小米、华为、美团、滴滴)和我自己整理Android复习笔记(包含Android基础知识点、Android扩展知识点、Android源码解析、设计模式汇总、Gradle知识点、常见算法题汇总。)
[外链图片转存中…(img-YsK4Dzix-1714506906521)]
《Android学习笔记总结+移动架构视频+大厂面试真题+项目实战源码》,点击传送门,即可获取!
- 相关阅读
- 二叉查找树中删除节点分析
- @author JackalTsc
- 代码15 二叉查找树的简单实现
- 代码14 后序遍历
- 代码13 中序遍历
- 代码12 先序遍历
- 代码10 二叉树的节点
- 性能分析
- 定义
- 树和二叉树的区别
- 三种遍历方法
- 相关性质
- 定义






还没有评论,来说两句吧...