机器学习——先验概率、后验概率、全概率公式、贝叶斯公式，机器学习中的概率公式，先验概率、后验概率、全概率与贝叶斯公式详解

摘要：机器学习领域中，先验概率和后验概率是贝叶斯推断的基础。先验概率反映了对未知事件的事先了解，而后验概率则是基于新数据对先验概率的调整。全概率公式用于计算事件发生的全面概率，而贝叶斯公式则用于更新先验概率，以反映新的证据或数据的影响。这些概念在机器学习领域具有重要的应用价值。

先验概率

定义：先验概率是根据以往经验和分析得到的概率，如全概率公式所示，通常作为“由因求果”问题中的“因”出现的概率。

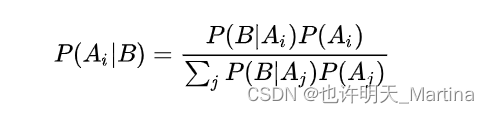
还要补充关于最大似然估计的内容：

最大似然估计：在多个可能的原因中，根据观察到的结果，计算每个原因导致这一结果的概率，然后选择概率最大的原因作为造成这一结果的最大原因，这种计算方式基于后验概率，有助于根据已知的结果分析最可能的原因，并针对性地解决问题。

参考：

先验概率与后验概率的相关知乎文章

简书上的贝叶斯公式的理解文章等。

对先验概率、后验概率、全概率公式和贝叶斯公式进行了详细的解释和补充，希望对你有所帮助。