Paillier 加法同态加密算法详细介绍，Paillier加法同态加密算法的详细介绍

摘要：本文介绍了Paillier加法同态加密算法，这是一种公钥加密算法，允许对密文进行加法运算而保持结果的加密状态。该算法基于复合剩余类问题的困难性，具有高度的安全性和实用性。通过详细介绍其原理、应用和优势，展示了Paillier算法在同态加密领域的重要性。

Paillier 加法同态加密算法详细介绍

文章目录

• Paillier 加法同态加密算法详细介绍
• • 1. 概述
  • 2. 原理
  • • 2.1 密钥生成
    • 2.2 加密
    • 2.3 解密
    • 3. Paillier 加密算法的解密过程
    • • 3.1 加密过程回顾
      • 3.2 解密步骤
      • 4. 同态特性
      • 5.批处理
      • 5. 安全性保障
      • 6. 结论
      • 7.代码附录

        1. 概述

        Paillier 同态加密算法是一种非对称加密算法，由 Pascal Paillier 在 1999 年提出。它的独特之处在于其同态特性，即能在加密数据上直接进行运算而无需解密。这使得它在数据隐私保护、安全多方计算等领域有着广泛的应用。

        
        （图片来源网络，侵删）

        2. 原理

        Paillier 加密算法主要包括三个部分：密钥生成、加密和解密。

        2.1 密钥生成

        1. 选择两个大素数 p p p 和 q q q: 这两个数越大，算法越安全。
        2. 计算 n = p × q n = p \times q n=p×q: 这是公钥的一部分。
        3. 计算 λ: λ 是 Carmichael’s totient 函数的输出，即 最小公倍数 lcm ( p − 1 , q − 1 ) \text{lcm}(p-1, q-1) lcm(p−1,q−1)。
        4. 选择一个整数 g: g 的选取应满足 g ∈ Z n 2 ∗ g \in \mathbb{Z}_{n^2}^* g∈Zn2∗​。

        公钥为 ( n , g ) (n, g) (n,g)，私钥为 λ \lambda λ。

        2.2 加密

        对于一个明文消息 m m m，加密过程如下：

        1. 选择一个随机数 r r r: r r r 是一个随机数，满足 r ∈ Z n ∗ r \in \mathbb{Z}_n^* r∈Zn∗​。
        2. 计算密文 c c c: 使用公钥 ( n , g ) (n, g) (n,g) 计算 c = g m × r n m o d    n 2 c = g^m \times r^n \mod n^2 c=gm×rnmodn2。

        2.3 解密

        对于一个密文 c c c，解密过程如下：

        1. 计算 u = c λ m o d    n 2 u = c^\lambda \mod n^2 u=cλmodn2。
        2. 计算 L ( u ) L(u) L(u): 其中 L L L 是一个特定的函数，定义为 L ( x ) = x − 1 n L(x) = \frac{x-1}{n} L(x)=nx−1​。
        3. 计算原始消息 m m m: 使用私钥 λ \lambda λ 和预先计算的 L ( g λ m o d    n 2 ) L(g^\lambda \mod n^2) L(gλmodn2) 的模逆元素，计算 m = L ( u ) × modinv ( L ( g λ m o d    n 2 ) , n ) m o d    n m = L(u) \times \text{modinv}(L(g^\lambda \mod n^2), n) \mod n m=L(u)×modinv(L(gλmodn2),n)modn。

        3. Paillier 加密算法的解密过程

        假设我们有密文 c c c，公钥 ( n , g ) (n, g) (n,g) 和私钥 λ \lambda λ。明文消息为 m m m，随机数 r r r 用于加密过程。

        3.1 加密过程回顾

        加密过程定义为：

        
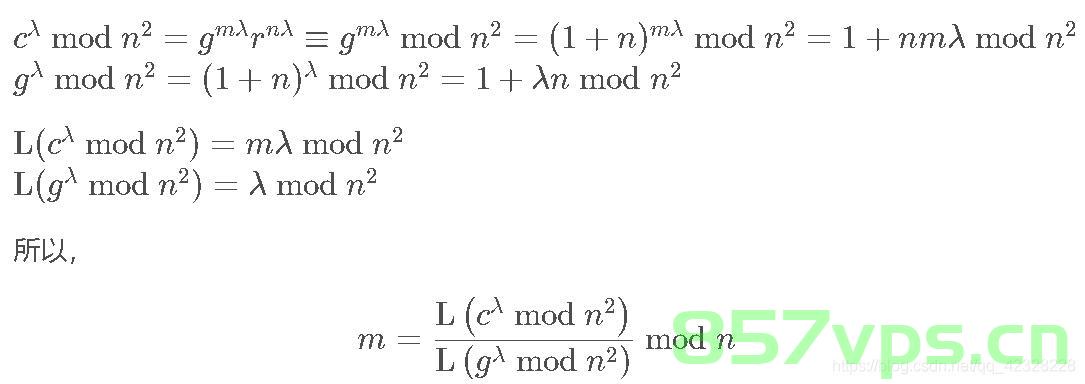        （图片来源网络，侵删）

        c = g m ⋅ r n m o d    n 2 c = g^m \cdot r^n \mod n^2 c=gm⋅rnmodn2

        3.2 解密步骤

        1. 计算 u u u

           首先计算 u = c λ m o d    n 2 u = c^\lambda \mod n^2 u=cλmodn2。由于 c = g m r n c = g^m r^n c=gmrn，我们有：

           u = ( g m r n ) λ m o d    n 2 u = (g^m r^n)^\lambda \mod n^2 u=(gmrn)λmodn2

        2. 利用 Carmichael 函数的性质

           由于 λ = lcm ( p − 1 , q − 1 ) \lambda = \text{lcm}(p-1, q-1) λ=lcm(p−1,q−1)，根据 Carmichael 函数的性质，对于任意 a ∈ Z n ∗ a \in \mathbb{Z}_n^* a∈Zn∗​：

           a λ ≡ 1 m o d    n a^\lambda \equiv 1 \mod n aλ≡1modn

           这意味着对于 r n r^n rn，有：

           ( r n ) λ ≡ 1 m o d    n 2 (r^n)^\lambda \equiv 1 \mod n^2 (rn)λ≡1modn2（把 r λ = k n + 1 r^\lambda = kn+1 rλ=kn+1带入展开）

        3. 分析 u u u 的表达式

           通过将 g m g^m gm 和 r n r^n rn 分开，我们可以重写 u u u 如下：

           u = ( g m ) λ ⋅ ( r n ) λ m o d    n 2 u = (g^m)^\lambda \cdot (r^n)^\lambda \mod n^2 u=(gm)λ⋅(rn)λmodn2

           我们可以将 u u u 简化为：

           u = ( g m ) λ ⋅ 1 m o d    n 2 u = (g^m)^\lambda \cdot 1 \mod n^2 u=(gm)λ⋅1modn2

           u = ( k n + 1 ) m m o d    n 2 u = (kn+1)^m \mod n^2 u=(kn+1)mmodn2

        4. 应用 L L L 函数

           接下来，我们应用 L L L 函数到 u u u 上。定义 L ( x ) = x − 1 n L(x) = \frac{x - 1}{n} L(x)=nx−1​，我们得到：

           L ( u ) = L ( ( k n + 1 ) m m o d    n 2 ) = [ ( k n + 1 ) m m o d    n 2 ] − 1 n = ( 1 + m ⋅ k n m o d    n 2 ) − 1 n = k m m o d    n 2 L(u) = L((kn+1)^m\mod n^2) = \frac{[(kn+1)^m\mod n^2] - 1}{n}=\frac{(1+m \cdot kn \mod n^2)-1}{n}=km \mod n^2 L(u)=L((kn+1)mmodn2)=n[(kn+1)mmodn2]−1​=n(1+m⋅knmodn2)−1​=kmmodn2

        5. 计算模逆元素 μ \mu μ

           在 Paillier 加密算法中，模逆元素 μ \mu μ是解密过程的关键部分。它是基于 g g g的一个特定幂的 L L L函数值的模逆元素。

           • 计算 L ( g λ m o d    n 2 ) L(g^\lambda \mod n^2) L(gλmodn2)

             首先，我们计算 g λ g^\lambda gλ在 m o d    n 2 \mod n^2 modn2下的结果，然后应用 L L L函数。根据 L L L函数的定义（ L ( x ) = x − 1 n L(x) = \frac{x - 1}{n} L(x)=nx−1​），我们有：

             L ( g λ m o d    n 2 ) = ( g λ m o d    n 2 ) − 1 n = ( 1 + k n m o d    n 2 ) − 1 n L(g^\lambda \mod n^2) = \frac{(g^\lambda \mod n^2) - 1}{n} =\frac{(1+kn \mod n^2) - 1}{n} L(gλmodn2)=n(gλmodn2)−1​=n(1+knmodn2)−1​

           • 计算 μ \mu μ

             接下来，我们计算 L ( g λ m o d    n 2 ) L(g^\lambda \mod n^2) L(gλmodn2)的模逆元素 μ \mu μ：

             μ = modinv ( L ( g λ m o d    n 2 ) , n ) \mu = \text{modinv}(L(g^\lambda \mod n^2), n) μ=modinv(L(gλmodn2),n)

             μ = [ ( 1 + k n m o d    n 2 ) − 1 n ] − 1 = ( k m o d    n 2 ) − 1 m o d    n \mu = [\frac{(1+kn \mod n^2) - 1}{n}]^{-1}=(k\mod n^2)^{-1}\mod n μ=[n(1+knmodn2)−1​]−1=(kmodn2)−1modn

             现在，计算原始消息 m m m

             m = L ( u ) × μ m o d    n m = L(u) \times \mu \mod n m=L(u)×μmodn

             因此，通过计算 L ( u ) × μ m o d    n L(u) \times \mu \mod n L(u)×μmodn，我们可以从加密后的 c c c中恢复出原始的明文消息 m m m。

        4. 同态特性

        Paillier 算法的主要特性是它的同态性质。具体来说，它支持同态加法和数乘操作：

        • 同态加法: 对于两个密文 c 1 c_1 c1​ 和 c 2 c_2 c2​，其解密结果等同于它们对应明文的和的加密，即 D ( E ( m 1 ) × E ( m 2 ) m o d    n 2 ) = m 1 + m 2 D(E(m_1) \times E(m_2) \mod n^2) = m_1 + m_2 D(E(m1​)×E(m2​)modn2)=m1​+m2​。
        • 同态加法（加密消息与明文整数）: 加密一个消息 m m m，然后将这个加密的结果与 g k m o d    n 2 g^k \mod n^2 gkmodn2（其中 g g g 是公钥的一部分）相乘。解密这个乘积将得到 m m m 与 k k k 的和,即 D ( E ( m ) × g k m o d    n 2 ) = m + k m o d    n \text{D}(E(m) \times g^k \mod n^2) = m + k \mod n D(E(m)×gkmodn2)=m+kmodn
        • 同态数乘: 对于一个密文 c c c 和一个明文数 k k k，其解密结果等同于密文对应明文的 k k k 倍的加密，即 D ( E ( m ) k m o d    n 2 ) = k × m D(E(m)^k \mod n^2) = k \times m D(E(m)kmodn2)=k×m。

          5.批处理

          我们可以将多个明文消息 m i m_i mi​ 批处理到同一个Paillier密文中，其中每个消息用 t t t 位表示。设 b b b 为批处理的大小，即我们可以在同一个Paillier密文中加密的正消息的最大数量为 c p = g m 1 + m 2 + . . . + m b ⋅ r N E   m o d   N E 2 c_p = g^{m_1 + m_2 + ... + m_b} \cdot r^{N_E} \bmod N^2_E cp​=gm1​+m2​+...+mb​⋅rNE​modNE2​，或者用不同的写法表示为 E n c ( m 1 ∣ m 2 ∣ . . . ∣ m b ) Enc(m_1 | m_2 | ... | m_b) Enc(m1​∣m2​∣...∣mb​)。为了正确解密 c p c_p cp​，需要满足 ∣ m 1 + m 2 + . . . + m b ∣ ≤ N E |m_1 + m_2 + ... + m_b| \leq N_E ∣m1​+m2​+...+mb​∣≤NE​ 和 b ≤ log ⁡ ( N E ) / t b \leq \log(N_E) / t b≤log(NE​)/t（即对于2048位的模数和消息位数 t = 64 t = 64 t=64 位，最多可以将32条消息打包在一起）。

          然而，如果我们想对这些打包的密文执行加法，必须考虑到这一点，以设置初始批次的维度，以避免溢出。设 n b add nb_{\text{add}} nbadd​ 为我们想要在这些打包的消息上执行的加法的数量。必须添加到每个插槽的填充（即零位数）等于 n b add nb_{\text{add}} nbadd​。因此，必须加密 E n c ( m 1 0...0 ⏟ nb add ∣ m 2 0...0 ⏟ nb add ∣ . . . ∣ m b 0...0 ⏟ nb add ) Enc(m_1\underbrace{0...0}_{\text{nb}_{\text{add}}} | m_2\underbrace{0...0}_{\text{nb}_{\text{add}}} | ... | m_b\underbrace{0...0}_{\text{nb}_{\text{add}}}) Enc(m1​nbadd​ 0...0​​∣m2​nbadd​ 0...0​​∣...∣mb​nbadd​ 0...0​​)。然后，批处理的大小最多应为 : b = ⌊ l o g 2 ( N E ) t + n b a   d d ⌋ :b=\left\lfloor{\frac{log_{2}(N_{E})}{t+nb_{a\:dd}}}\right\rfloor :b=⌊t+nbadd​log2​(NE​)​⌋。

          让我们举一个简短的例子。假设我们要加密的每条消息是介于0和U之间的实际正数，其中U = 100，且 m i m_i mi​ 在小数点后有4位有效数字。因此，为了表示这些消息，必须至少有 $\lceil{log_{2}}(U*10^{4})\rceil $，即20位。对于这种类型的消息，对密文执行两次加法（每次加法需要填充1位），对于2048位的模数，可以将93条消息打包在单个密文中。对于相同格式的密文执行100次加法，每个密文最多可以有17个插槽。

          ⌈ log ⁡ 2 ( U × 1 0 4 ) ⌉ = ⌈ log ⁡ 2 ( 100 × 1 0 4 ) ⌉ = ⌈ log ⁡ 2 ( 1 0 6 ) ⌉ = ⌈ 20 ⌉ = 20 \lceil \log_2(U \times 10^4) \rceil = \lceil \log_2(100 \times 10^4) \rceil = \lceil \log_2(10^6) \rceil = \lceil 20 \rceil = 20 ⌈log2​(U×104)⌉=⌈log2​(100×104)⌉=⌈log2​(106)⌉=⌈20⌉=20

          5. 安全性保障

          Paillier 算法的安全性主要依赖于大数分解的困难性。当选择的素数 p p p 和 q q q 足够大时，要破解该算法需要解决一个非常困难的数学问题——大数分解问题。因此，在实际应用中，应确保 p p p 和 q q q 的选取足够安全。

          6. 结论

          Paillier 加密算法由于其同态特性，在多方安全计算、数据隐私保护、云计算安全等领域有着重要应用。例如，在电子投票系统中，可以保证投票的隐私性和可验证性；在数据分析中，可以对加密数据进行处理而无需暴露原始数据。

          Paillier 同态加密算法提供了一种在加密状态下进行计算的能力，对于保护数据隐私和安全性有着重要意义。尽管其计算过程相对复杂，但它的安全性和独特的同态特性使其在现代加密应用中占有一席之地。

          7.代码附录

          import random
          from sympy import isprime, mod_inverse
          import gmpy2
          def generate_prime_candidate(length):
              """ 随机生成一个指定长度的奇数 """
              p = random.getrandbits(length)  # 获取一个指定长度的随机位
              p |= (1