温馨提示:这篇文章已超过447天没有更新,请注意相关的内容是否还可用!
摘要:本研究探讨了数学建模在天然肠衣搭配问题中的应用。针对肠衣生产过程中的不同材质、尺寸和性能要求,通过建立数学模型,优化肠衣的搭配方案。研究旨在提高肠衣产品的质量和生产效率,同时降低成本。通过数学建模,为肠衣行业提供科学的搭配依据,推动行业的技术进步和可持续发展。
2011高教社杯全国大学生数学建模竞赛D题
天然肠衣(以下简称肠衣)制作加工是我国的一个传统产业,出口量占世界首位。肠衣经过清洗整理后被分割成长度不等的小段(原料),进入组装工序。传统的生产方式依靠人工,边丈量原料长度边心算,将原材料按指定根数和总长度组装出成品(捆)。
原料按长度分档,通常以0.5米为一档,如:3-3.4米按3米计算,3.5米-3.9米按3.5米计算,其余的依此类推。表1是几种常见成品的规格,长度单位为米,∞表示没有上限,但实际长度小于26米。
\space \space \space \space \space \space \space 表1 成品规格表
| 最短长度 | 最大长度 | 根数 | 总长度 |
|---|---|---|---|
| 3 | 6.5 | 20 | 89 |
| 7 | 13.5 | 8 | 89 |
| 14 | ∞ ∞ ∞ | 5 | 89 |
为了提高生产效率,公司计划改变组装工艺,先丈量所有原料,建立一个原料表。表2为某批次原料描述。
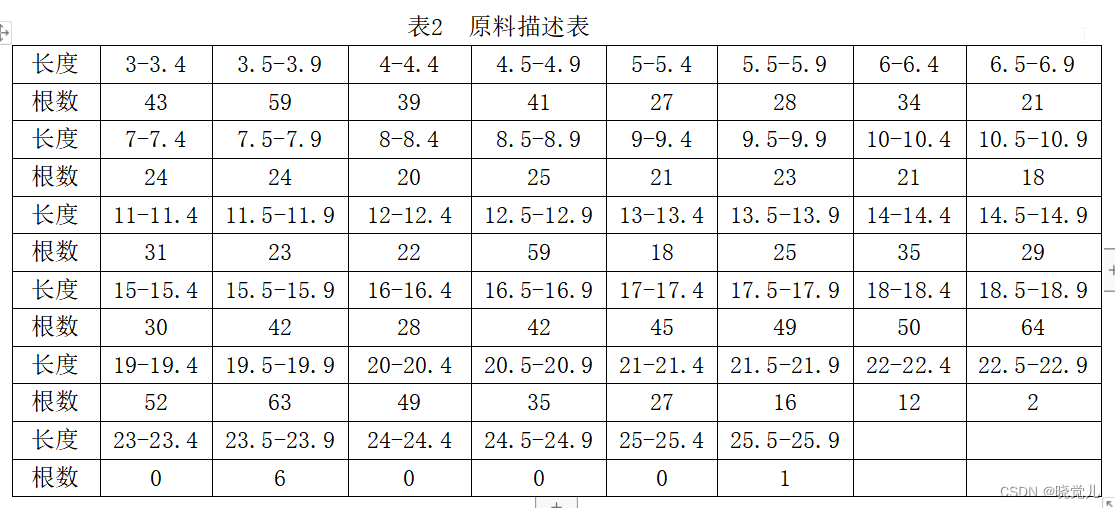
根据以上成品和原料描述,设计一个原料搭配方案,工人根据这个方案“照方抓药”进行生产。
公司对搭配方案有以下具体要求:
(1) 对于给定的一批原料,装出的成品捆数越多越好;
(2) 对于成品捆数相同的方案,最短长度最长的成品越多,方案越好;
(3) 为提高原料使用率,总长度允许有
天然肠衣搭配问题
- 提出假设
- 问题简单复述:
- 对应每一个任意种类的成品建立第一种模型
- 基于成品分配方案的第二种模型
- 模型二总结
- 手动实现局部最优解
- 局部最优解
提出假设
假设降级使用仅可降一级,不可多级降,如如长度为14米的原料不可以和长度介于3-6.5米的进行捆扎
问题简单复述:
用以0.5米为一档给出的原料按指定根数和总长度组装出成品,为此设计一个原料搭配方案。
方案好坏比较首先是装出的成品捆数越多越好;其次捆数相同的方案,最短长度为14的成品越多,方案越好
使用附带原则有总长度允许有 ± 0.5 ± 0.5 ±0.5米的误差,总根数允许比标准少 1 1 1根;某种规格对应原料如果出现剩余,可以降级使用。
建立数学模型:
首先考虑装出的成品捆数,设三种不同最短长度(从小到大)的成品个数依次为 x 1 , x 2 , x 3 x_1,x_2,x_3 x1,x2,x3
装出的成品捆数越多越好有:
m a x = ∑ 1 ≤ i ≤ 3 x i max = \sum_{1 \le i \le 3} x_i max=∑1≤i≤3xi
为了简化问题,解决最短长度为14的成品越多,方案越好的方案为:
设已求得一组可行解 x 1 ′ , x 2 ′ , x 3 ′ x_1',x_2',x_3' x1′,x2′,x3′
加入限制条件
x 3 > x 3 ′ x_3 > x_3' x3>x3′
考虑原料如果出现剩余,可以降级使用。那么解决顺序应该是成品三,成品二,成品一。
因为每个成品最短长度到最长长度的区间没有重叠,所以三个成品可以分开讨论。
对应每一个任意种类的成品建立第一种模型
设原料按长度由小到大的使用个数依次为 y 1 , y 2 , . . . , y n y_1 ,y_2 ,...,y_n y1,y2,...,yn,总长度为 a a a,根数为 b i ′ b_{i'} bi′,最小大长度 c i ′ c_{i'} ci′,最大长度 c j ′ c_{j'} cj′
都要满足
成品总长度在标准的 ± 0.5 ± 0.5 ±0.5米误差范围内:
a − 0.5 ≤ ( 3 + 0.5 ( i − 1 ) ) y i + ( 3 + 0.5 i ) y i + 1 + . . . ( 3 + 0.5 ( j − 1 ) ) y j ≤ a + 0.5 a-0.5 \le (3+0.5(i-1))y_i+(3+0.5i)y_{i+1}+...(3+0.5(j-1))y_j \le a+0.5 a−0.5≤(3+0.5(i−1))yi+(3+0.5i)yi+1+...(3+0.5(j−1))yj≤a+0.5
总根数和标准一致或总根数比标准少 1 1 1根:
y i + y i + 1 + . . . + y j = b i ′ − z , z = 0 / 1 y_i + y_{i+1} + ... +y_j = b_{i'}-z , z = 0/1 yi+yi+1+...+yj=bi′−z,z=0/1
使用的原料长度在成品规格表的标准长度范围内
2 ( c i ′ − 3 ) − 1 ≤ y k ≤ 2 ( c j ′ − 3 ) − 1 , i ≤ k ≤ j 2(c_{i'} - 3) -1 \le y_k\le 2(c_{j'} - 3) -1 , i\le k \le j 2(ci′−3)−1≤yk≤2(cj′−3)−1,i≤k≤j
考虑原料如果出现剩余,可以降级使用。我们设上一级(如果有的话)的的最大长度为 c j ′ + 1 c_{j'+1} cj′+1
2 ( c i ′ − 3 ) − 1 ≤ y k ≤ 2 ( c j ′ + 1 − 3 ) − 1 , i ≤ k ≤ j 2(c_{i'} - 3) -1 \le y_k\le 2(c_{j'+1} - 3) -1 , i\le k \le j 2(ci′−3)−1≤yk≤2(cj′+1−3)−1,i≤k≤j
因为做出一个成品,对应使用的原料数量会降低,设原料按长度由小到大的减少总个数依次为 u 1 , u 2 , . . . , u n u_1 ,u_2 ,...,u_n u1,u2,...,un,原料按长度由小到大的总个数依次为 d 1 d 2 , . . . , d n d_1 d_2 ,...,d_n d1d2,...,dn
我们要满足每一次原料都不能凭空产生
y i ≤ d i − u i , 1 ≤ i ≤ n y_i \le d_i - u_i ,1 \le i \le n yi≤di−ui,1≤i≤n
并且当满足 { a − 0.5 ≤ ( 3 + 0.5 ( i − 1 ) ) y i + ( 3 + 0.5 i ) y i + 1 + . . . ( 3 + 0.5 ( j − 1 ) ) y j ≤ a + 0.5 y i + y i + 1 + . . . + y j = b i − z , z = 0 / 1 2 ( c i ′ − 3 ) − 1 ≤ y k ≤ 2 ( c j ′ + 1 − 3 ) − 1 , i ≤ k ≤ j y i ≤ d i − u i , 1 ≤ i ≤ n \begin{cases} a-0.5 \le (3+0.5(i-1))y_i+(3+0.5i)y_{i+1}+...(3+0.5(j-1))y_j \le a+0.5\\ y_i + y_{i+1} + ... +y_j = b_i-z , z = 0/1 \\ 2(c_{i'} - 3) -1 \le y_k\le 2(c_{j'+1} - 3) -1 , i\le k \le j \\ y_i \le d_i - u_i ,1 \le i \le n \end{cases} ⎩ ⎨ ⎧a−0.5≤(3+0.5(i−1))yi+(3+0.5i)yi+1+...(3+0.5(j−1))yj≤a+0.5yi+yi+1+...+yj=bi−z,z=0/12(ci′−3)−1≤yk≤2(cj′+1−3)−1,i≤k≤jyi≤di−ui,1≤i≤n的时候对应种类的成品数量加一,即 x i = x i + 1 x_i=x_i+1 xi=xi+1,并且原材料使用后对应的原材料数目减少,即 u i = u i + y i , 1 ≤ i ≤ n u_i =u_i+y_i , 1 \le i \le n ui=ui+yi,1≤i≤n
C++
#include #include #include using namespace std; int cnt[] ={43,59,39,41,27,28,34,21,24,24,20,25,21,23,21,18,31,23,22,59,18,25,35,29,30,42,28,42,45,49,50,64,52,63,49,35,27,16,12,2,0,6,0,0,0,1}; // 3+0.5i int x[4]; int x_3 = 0;//已知x3的最大解 void solve(); double min_size = 3,max_size =6.5,total_size =89; int roots_Number = 20; int f_xi = 1; double now_total_size=0; int now_roots_Number = 0; void f( int k ,int u){ if(now_total_size = total_size - 0.5){ if(now_roots_Number == roots_Number || now_roots_Number == roots_Number-1){ x[f_xi] = max(x[f_xi],u+1); double kt = now_total_size;int kr = now_roots_Number; now_total_size = now_roots_Number = 0; f(((int)max_size - 3)*2,u+1); now_total_size = kt , now_roots_Number = kr; return ; } else return ; } //if(now_total_size>0.5 + total_size)return ; // cut down #if 0 //small to big if(3+0.5*k > max_size)return ; // can't chose int ct = min(cnt[k] ,(int)((total_size - now_total_size)/(3+0.5*k))); for(int i=0;i roots_Number)return ; for(int i=0;i 137; @for(bb(i):@gin(y(i))); @for(bb(i):y(i)>0); @for(aa(i):d(i)>@sum(bb(j):y(j)*z(j,i))); @for(aa(i):u(i) = d(i)-@sum(bb(j):y(j)*z(j,i))); !成品二 @sum(dd(i):x(i)) > ...;!求成品三后成品二最大组成数量+ @for(dd(i):@gin(x(i))); @for(dd(i):x(i)>0); @for(aa(i):u(i)>@sum(dd(j):x(j)*e(j,i))); @for(aa(i):v(i) = d(i)-@sum(dd(j):x(j)*e(j,i))); !成品一 @for(ff(i):@gin(f(i))); @for(ff(i):f(i)>0); @for(aa(i):v(i)>@sum(ff(j):f(j)*h(j,i))); max = @sum(bb(i):y(i)) + @sum(dd(j):x(j)) + @sum(dd(j):x(j));需要在C++/其他程序中跑出成品一的2861814种方案的列表和成品二的466598种方案的列表。加在上述代码中。或者用其他方式给e和f赋值
e = ... !成品二的方案 h = ... !成品一的方案
模型二总结
思路总结:配完成品三,得出剩余的原材料数量,再配成品二,得出剩余原材料数量,最后配成品一。最后得到最优配比
目前的问题:无法有效的解决剩余这个关键,剩余条件为剩下的无法组成任何一种成品方案。
仅靠代码@sum(bb(i):y(i)) > 137;去约束剩余这个条件,只是局部最优,而不一定是全局最优
代码优化思路:例如成品三对于前面20多个都没用,直接优化掉;成品二一同上
难点:目前已知成品一方案数多达百万量级
手动实现局部最优解
虽然得出的答案不一定是全局最优,但可以先试试手动模拟成品三,二,一的步骤,先得出一种(多种)局部最优。如果有规律或者新的上限模型,就可以推出某一个局部最优解即是全局最优
按照模型二跑一次成品三
Objective value: 137.0000 Objective bound: 137.0000 U( 30) 1.000000 0.000000
长度范围为 17.5 − 17.9 17.5-17.9 17.5−17.9剩余1根
将剩余的长度的带入,得出成品二的分配方案有12729种,相比于带入无处理成品三后数据的直接计算的分配方案少了一个量级。
将成品二的分配方案带入模型和程序中得:
Objective value: 37.00000 Objective bound: 37.00000 U( 1) 43.00000 0.000000 U( 2) 59.00000 0.000000 U( 3) 39.00000 0.000000 U( 4) 41.00000 0.000000 U( 5) 27.00000 0.000000 U( 6) 28.00000 0.000000 U( 7) 34.00000 0.000000 U( 8) 21.00000 0.000000 U( 9) 23.00000 0.000000 U( 10) 23.00000 0.000000 U( 11) 7.000000 0.000000 U( 12) 1.000000 0.000000 U( 14) 2.000000 0.000000 U( 15) 2.000000 0.000000 U( 17) 1.000000 0.000000将剩余的长度的带入,得出成品一的分配方案有1213327种,相比于带入无处理成品二后数据的直接计算的分配方案量级没变。
但如果不算降级处理的东西分配方案仅有59942种
单独解决成品一:
Global optimal solution found. Objective value: 14.00000 Objective bound: 14.00000 Infeasibilities: 0.000000 Extended solver steps: 0 Total solver iterations: 8821 Variable Value Reduced Cost U( 2) 5.000000 0.000000 U( 4) 6.000000 0.000000 U( 5) 1.000000 0.000000 U( 6) 3.000000 0.000000 U( 9) 23.00000 0.000000 U( 10) 23.00000 0.000000 U( 11) 7.000000 0.000000 U( 12) 1.000000 0.000000 U( 14) 2.000000 0.000000 U( 15) 2.000000 0.000000 U( 17) 1.000000 0.000000局部最优解
成品三137个,成品二37个,成品三14个,总188个
- 局部最优解






还没有评论,来说两句吧...