数学建模 --- Lingo 钢管下料问题，数学建模，解决Lingo钢管下料问题的策略与方法

摘要：本文研究了钢管下料问题的数学建模，采用Lingo软件进行优化。通过构建线性规划模型，解决了在特定条件下如何合理下料以最大化材料利用率的问题。Lingo软件的运用使得复杂的数学模型得以快速求解，为钢管下料提供了有效的决策支持。该问题的解决对于提高生产效率、降低成本具有重要意义。

每根19米。

客户需求：需要4米50根，6米20根，8米15根。

问题1：如何切割原料钢管以使得剩余总余量最小？

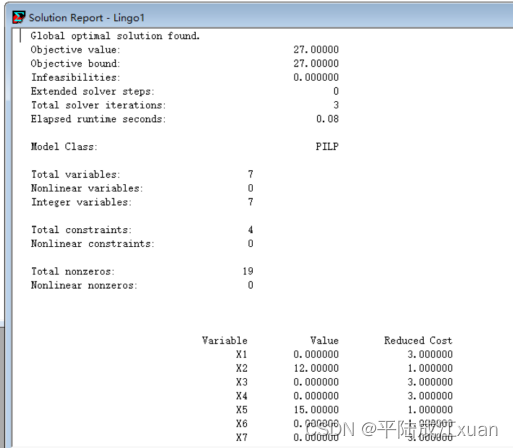
方法1：数学建模方式

建立数学模型以最小化剩余余量，可以设立一系列变量x_i表示切割出的不同长度的钢管数量，然后建立约束条件以满足客户的需求，通过求解这个优化问题，可以得到切割方案，使得剩余余量最小，具体的数学模型和公式较为复杂，这里不再赘述。

方法2：集合和循环方式

可以使用集合和循环的方式来描述这个问题，设定集合来表示不同的钢管长度和切割模式，然后使用数据来描述客户需求，通过循环和约束条件来满足客户需求，并尝试找到剩余余量最小的切割方案，具体的实现方式需要借助编程语言和优化工具。

问题2：当客户需求增加5米10根时，如何保证用到钢材根数最少？

在原有需求的基础上，增加了对5米长度钢管的需求（10根），这时需要考虑如何在满足新需求的同时，尽量减少使用的钢材根数。

模型建立：

定义变量x_i表示切割出的不同长度钢管的数量。

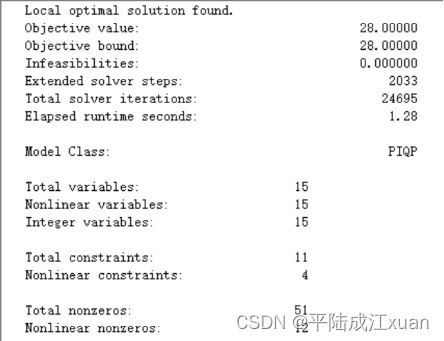
约束条件满足新的客户需求，即5米的10根、4米的50根、6米的20根、8米的15根。

最小化目标使用的钢材根数最少，可以通过优化模型来求解这个最小化问题。

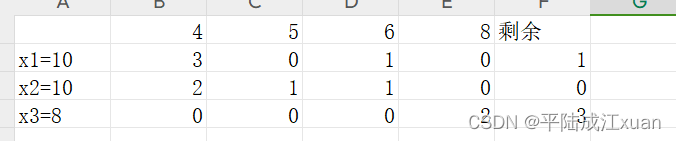
切割模式与结果：

通过求解优化模型，可以得到最佳的切割模式以及使用的钢材根数最少的结果，具体的切割模式和结果需要根据求解优化模型得出，可能需要考虑的因素包括切割顺序、切割点的选择等，以最小化浪费并满足客户需求。

注：以上内容仅提供了问题的描述和初步的分析，具体的数学模型、公式和解决方案需要进一步的深入研究和计算。