【C语言】数据的存储，C语言中的数据存储之道

摘要：，，本文简要介绍了C语言中数据的存储。在C语言中，数据的存储涉及到内存管理和数据类型。变量在内存中占据一定的空间，不同类型的数据占用不同的内存空间大小。了解内存分配和数据类型对于有效地使用C语言进行编程至关重要，有助于开发人员更好地管理数据，确保程序的正确运行和效率。

3.1415926

1E10 （即10的10次方）

浮点型包括：float、double、long double类型。

浮点数表示的范围和精度在float.h中定义，要理解浮点数在计算机内部的表示方法，我们需要知道其存储规则。

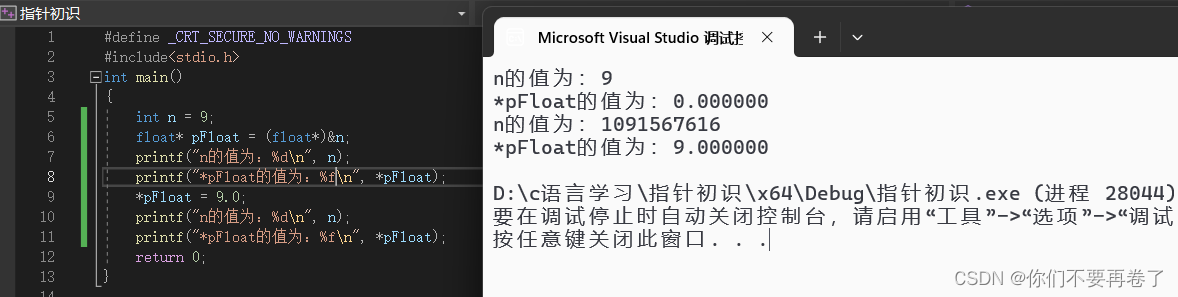
浮点数存储的一个常见误区是，即使看起来两个数值在外部表示中几乎相同（例如n和*pFloat），但在内部以二进制形式解读时，由于浮点数的特殊编码方式，它们可能表示完全不同的数值。

根据国际标准IEEE（电子和电子工程协会）754，任意一个二进制浮点数V可以表示成以下形式：

(-1)^S * M * 2^E

(-1)^S表示符号位，当S=0时，V为正数；当S=1时，V为负数。

M表示有效数字，大于等于1，小于2。

2^E表示指数位。

举个例子：

V=5.0，转化为二进制是101.0，再写成科学计数法的形式即1.01 * 2^2，所以它可以表示为(-1)^0 * 1.01 * 2^2。

V=9.5，转化为二进制是1001.1，科学计数法为1.0011 * 2^3，即(-1)^0 * 1.0011 * 2^3。

值得注意的是，某些浮点数（如9.6）在转化为二进制时可能会遇到精度丢失的问题，因为小数部分在二进制中的表示并不总是精确的，这就是为什么我们说浮点数在内存中可能无法精确保存的原因，double类型的精度显然要比float高。

对于32位的浮点数，IEEE 754规定最高位的1位是符号位S，接着的8位是指数E，剩下的23位为有效数字M，而对于64位的浮点数，符号位S有1位，指数E有11位，有效数字M有52位。

关于有效数字M和指数E有一些特殊规定，有效数字M的值是大于等于1，小于2的，因此可以写成1.xxxxxxxx的形式，在计算机内部保存M时，默认数的第一位总是1，因此可以被舍去，只保存后面xxxxxx的部分，这样做的目的是节省有效数字的位数，指数E在实际存储时需要加上一个中间值（对于8位的E，这个中间值是127；对于11位的E，这个中间值是1023），以得到真实的指数值。

关于浮点数的存储例子和整数与浮点数之间的转换关系已经很详细地解释了，理解这些规则对于理解计算机如何处理近似值以及编写处理浮点数的代码非常重要。