目标跟踪—卡尔曼滤波，卡尔曼滤波在目标跟踪中的应用

温馨提示：这篇文章已超过436天没有更新，请注意相关的内容是否还可用！

摘要：卡尔曼滤波是一种广泛应用于目标跟踪的技术。它通过递归算法，结合系统模型的预测和传感器的观测数据，对目标状态进行最优估计。卡尔曼滤波能够处理噪声和不确定性，并在动态环境中实现准确的目标跟踪。这一技术在军事、自动驾驶、机器人导航等领域有着广泛的应用前景。

目标跟踪—卡尔曼滤波

卡尔曼滤波引入

目标跟踪—卡尔曼滤波，卡尔曼滤波在目标跟踪中的应用第1张

滤波是将信号中特定波段频率滤除的操作，是抑制和防止干扰的一项重要措施。是根据观察某一随机过程的结果，对另一与之有关的随机过程进行估计的概率理论与方法。

历史上最早考虑的是维纳滤波，后来R.E.卡尔曼和R.S.布西于20世纪60年代提出了卡尔曼滤波。现对一般的非线性滤波问题的研究相当活跃。

简单的理解滤波的作用是处理高斯噪声使得数据变得更加的平滑

适用系统

适用系统线性高斯系统：线性满足：叠加性和齐次性即为：

y = a x 1 + b x 2 y=a x_{1}+b x_{2} y=ax1+bx2

高斯：噪声满足高斯分布。

一般情况下的理想状态为: 信号 x 1 + 噪声 x 0 在使用卡尔曼滤波的情况下。修正值= w1 x 估计值 + w2 x 观察值。

且满足 w1+ w2 = 1的条件

卡尔曼滤波基础准备

状态空间表达式

状态方程：

x k = A x k − 1 + B u k + ω k {x_{k}}=A x_{k-1}+B u_{k}+\omega_{k} xk=Axk−1+Buk+ωk

xk：表示当前状态的当前值 K代表当前的状态信息
xk-1：表示上一个状态的当前值 K-1代表上一个状态信息
wk：表示过程噪声
uk:表示的是一个输入信息
A：表示的是一个状态转移矩阵
B：表示的是一个控制矩阵
观测方程：
y k = C x k + v k y_{k}=C x_{k}+v_{k} yk=Cxk+vk
- yk:表示要观测的值
- vk:表示一个过程噪声（与观察器误差有关可以简单理解为误差）
- xk：表示当前状态的当前值 K代表当前的状态信息
  参数分析
  高斯白噪声：满足期望为0的高斯分布
  w k ∈ N ( 0 ; Q k ) V k ∈ N ( 0 ; R k ) \begin{array}{l} w_{k} \in N\left(0 ; Q_{k}\right) \\ V_{k} \in N\left(0 ; R_{k}\right) \end{array} wk∈N(0;Qk)Vk∈N(0;Rk)
  其中Q：代表过程噪声的方差，R:代表观测噪声的方差。是在算法实现过程中的超参数
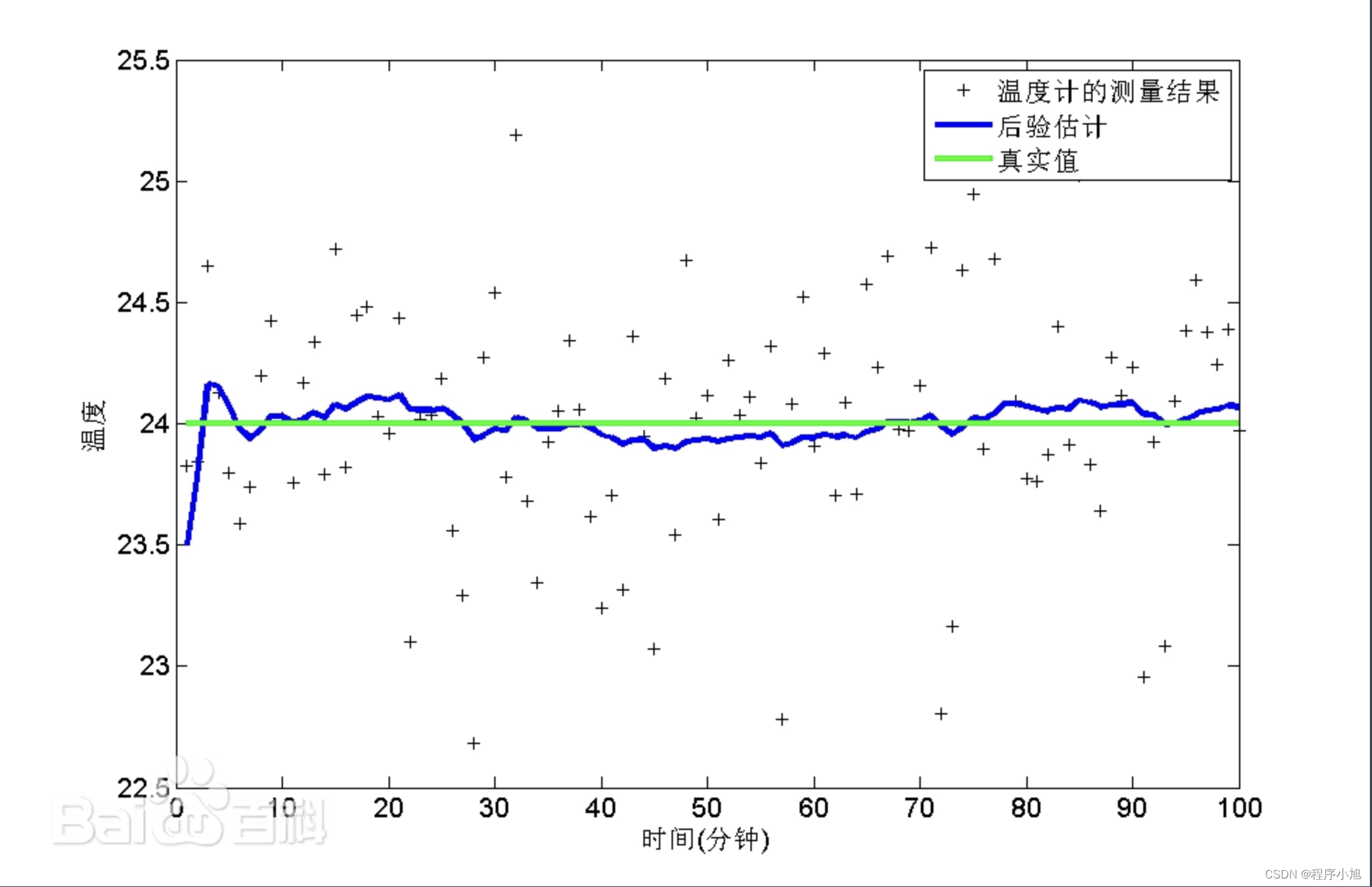
  下面是卡尔曼滤波的直观图解
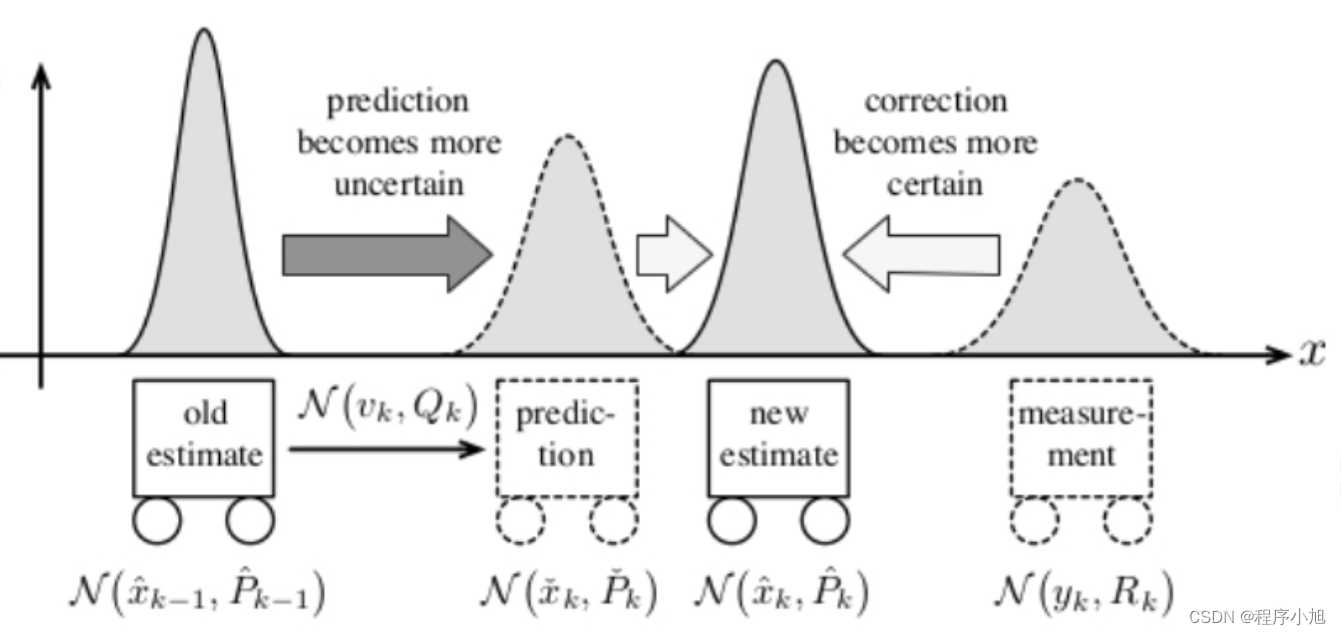
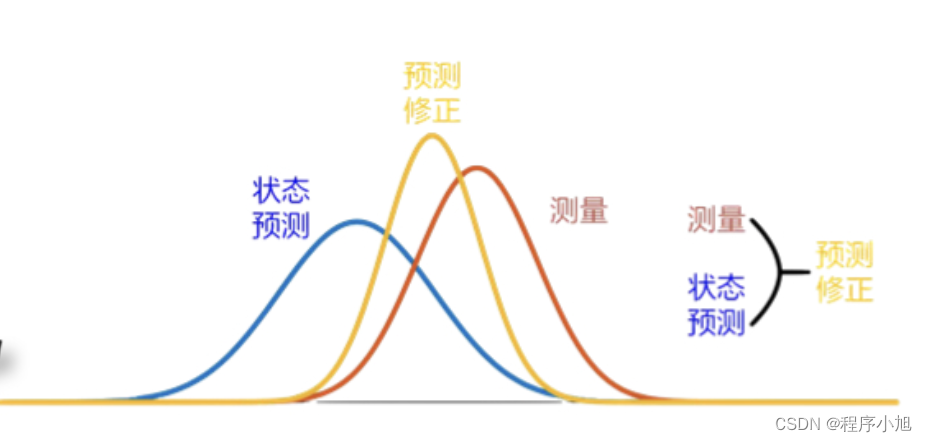
  卡尔曼滤波的理论
  卡尔曼滤波的理解：
  实现过程: 使用上一次的最优结果预测当前的值,同时使用观测值****修正当前值,得到最优结果(可以简单理解为是一个递归的过程)
  1. 在预测过程中使用到的公式
    x ^ t − = F x ^ t − 1 + B u t − 1 P t − = F P t − 1 F T + Q \begin{array}{l} \hat{x}_{t}^{-}=F \hat{x}_{t-1}+B u_{t-1} \\ P_{t}^{-}=F P_{t-1} F^{T}+Q \end{array} x^t−=Fx^t−1+But−1Pt−=FPt−1FT+Q
  其中P(t)对应的是x的协方差矩阵，而其中的x-表示的就是一个预测估计
  1. 在更新过程中使用到的公式
    K t = P t − H T ( H P t − H T + R ) − 1 x ^ t = x ^ t − + K t ( z t − H x ^ t − ) P t = ( I − K t H ) P t − \begin{array}{l} K_{t}=P_{t}^{-} H^{T}\left(H P_{t}^{-} H^{T}+R\right)^{-1} \\ \hat{x}_{t}=\hat{x}_{t}^{-}+K_{t}\left(z_{t}-H \hat{x}_{t}^{-}\right) \\ P_{t}=\left(I-K_{t} H\right) P_{t}^{-} \end{array} Kt=Pt−HT(HPt−HT+R)−1x^t=x^t−+Kt(zt−Hx^t−)Pt=(I−KtH)Pt−
  z(t)表示的就是一个观测值 K:表示的是卡尔曼增益，在更新的过程中就涉及到了预测值的更新，与协方差矩阵的更新
  先验估计的简单理解
  x ^ t − = F x ^ t − 1 + B u t − 1 \hat{x}_{t}^{-}=F \hat{x}_{t-1}+B u_{t-1} \\ x^t−=Fx^t−1+But−1
  其中的F即为状态转移矩阵 B即为控制矩阵
  首先以匀加速直线运动为例化为状态方程的形式来进行表示
  P i = P i − 1 + v i − 1 ⋅ Δ t + a 2 Δ t 2 v i = v i − 1 + a ⋅ Δ t } ⇒ [ p i v i ] = [ 1 Δ t 0 1 ] [ p i − 1 v i − 1 ] + [ Δ t 2 2 Δ t ] a i \left.\begin{array}{l} P_{i}=P_{i-1}+v_{i-1} \cdot \Delta t+\frac{a}{2} \Delta t^{2} \\ v_{i}=v_{i-1}+a \cdot \Delta t \end{array}\right\} \Rightarrow\left[\begin{array}{l} p_{i} \\ v_{i} \end{array}\right]=\left[\begin{array}{cc} 1 & \Delta t \\ 0 & 1 \end{array}\right]\left[\begin{array}{l} p_{i-1} \\ v_{i-1} \end{array}\right]+\left[\begin{array}{c} \frac{\Delta t^{2}}{2} \\ \Delta t \end{array}\right] a_{i} Pi=Pi−1+vi−1⋅Δt+2aΔt2vi=vi−1+a⋅Δt}⇒[pivi]=[10Δt1][pi−1vi−1]+[2Δt2Δt]ai
  先验估计的协方差
  P t − = F P t − 1 F T + Q P_{t}^{-}=F P_{t-1} F^{T}+Q Pt−=FPt−1FT+Q
  根据先验估计得到协方差的推导过程如下：
  cov ⁡ ( x ^ t − , x ^ t − ) = cov ⁡ ( F x ^ t − 1 + B u t − 1 , F x ^ t − 1 + B u t − 1 ) + Q = F cov ⁡ ( x ^ t − 1 , x ^ t − 1 ) F ⊤ + Q \begin{array}{l} \operatorname{cov}\left(\hat{x}_{t}^{-}, \hat{x}_{t^{-}}\right)=\operatorname{cov}\left(F \hat{x}_{t-1}+B u_{t-1}, F \hat{x}_{t-1}+B u_{t-1}\right) \\ +Q=F \operatorname{cov}\left(\hat{x}_{t-1}, \hat{x}_{t-1}\right) F^{\top} +Q \\ \end{array} cov(x^t−,x^t−)=cov(Fx^t−1+But−1,Fx^t−1+But−1)+Q=Fcov(x^t−1,x^t−1)F⊤+Q
  从而得到了先验估计协方差的形式（带过程噪声的形式）
  状态更新
  通过修正估计得到卡尔曼滤波的最终值(最终滤波结果)
  x ^ t = x ^ t − + K t ( z t − H x ^ t − ) P t = ( I − K t H ) P t − \hat{x}_{t}=\hat{x}_{t}^{-}+K_{t}\left(z_{t}-H \hat{x}_{t}^{-}\right) \\ P_{t}=\left(I-K_{t} H\right) P_{t}^{-} x^t=x^t−+Kt(zt−Hx^t−)Pt=(I−KtH)Pt−
  核心需要用到卡尔曼增益与测量值，需要计算测量值-预测值*H
  其中H表示观测矩阵的值
  其中卡尔曼增益的表示形式为：
  K t = p t − H ⊤ H p t − H ⊤ + R K_{t}=\frac{p_{t}^{-} H^{\top}}{H p_{t}^{-} H^{\top}+R} Kt=Hpt−H⊤+Rpt−H⊤
  根据观测值和预测值的噪声调节对应的权重值k
  P t − = F P t − 1 F − 1 + Q k = P t − H ⊤ H P t − H ⊤ + R } → 化简 k = P t − 1 + Q P t − 1 + Q + R \left.\begin{array}{l} P_{t}^{-}=F P_{t-1} F^{-1}+Q \\ k=\frac{P_{t}^{-} H^{\top}}{H P_{t}^{-} H^{\top}+R} \end{array}\right\} \xrightarrow{\text { 化简 }} k=\frac{P_{t-1}+Q}{P_{t-1}+Q+R} Pt−=FPt−1F−1+Qk=HPt−H⊤+RPt−H⊤} 化简 k=Pt−1+Q+RPt−1+Q
  卡尔曼滤波推导
  首先建立已知的现实空间中的状态空间：
  x k = A x k − 1 + B u k − 1 + w k − 1 , P ( w ) ∼ ( 0 , Q ) , Q = E [ w w T ] z k = H x k + v k , P ( v ) ∼ ( 0 , R ) E [ w w T ] = E [ ( w 1 w 2 ) ( w 1 w 2 ) ] = [ E ( w 1 2 ) E ( w 1 w 2 ) E ( w 1 w 2 ) E ( w 2 2 ) ] = [ σ ( w 1 2 ) σ ( w 1 w 2 ) σ ( w 1 w 2 ) σ ( w 2 2 ) ] \begin{array}{c} x_{k}=A x_{k-1}+B u_{k-1}+w_{k-1}, \mathrm{P}(\mathrm{w}) \sim(0, \mathrm{Q}), \mathrm{Q}=\mathrm{E}\left[\mathrm{w} w^{T}\right] \\ z_{k}=H x_{k}+v_{k}, \mathrm{P}(\mathrm{v}) \sim(0, \mathrm{R}) \\ \mathrm{E}\left[\mathrm{w} w^{T}\right]=\mathrm{E}\left[\binom{w_{1}}{w_{2}}\left(\begin{array}{ll} w_{1} & \left.w_{2}\right) \end{array}\right]=\left[\begin{array}{cc} E\left(w_{1}^{2}\right) & E\left(w_{1} w_{2}\right) \\ E\left(w_{1} w_{2}\right) & E\left(w_{2}{ }^{2}\right) \end{array}\right]=\left[\begin{array}{cc} \sigma\left(w_{1}^{2}\right) & \sigma\left(w_{1} w_{2}\right) \\ \sigma\left(w_{1} w_{2}\right) & \sigma\left(w_{2}^{2}\right) \end{array}\right]\right. \end{array} xk=Axk−1+Buk−1+wk−1,P(w)∼(0,Q),Q=E[wwT]zk=Hxk+vk,P(v)∼(0,R)E[wwT]=E[(w2w1)(w1w2)]=[E(w12)E(w1w2)E(w1w2)E(w22)]=[σ(w12)σ(w1w2)σ(w1w2)σ(w22)]
  其中核心在于Q表示的是协方差矩阵，可以通过w向量的形式写成，协方差矩阵的形式
  同理vk也符合同样的分布模型
  实际的状态空间模型
  x ^ k ′ = A x ^ k − 1 + B u k − 1 z k = H x k → x ^ k = H ′ z k ′ \begin{array}{c} \hat{x}_{k}{ }^{\prime}=A \widehat{x}_{k-1}+B u_{k-1} \\ z_{k}=H x_{k} \rightarrow \widehat{x}_{k}=H^{\prime} z_{k^{\prime}} \end{array} x^k′=Ax k−1+Buk−1zk=Hxk→x k=H′zk′
  我们建模中不知道的便是 ω \omega ω 和 v v v , 其余的矩阵是已知的, 而我们通过 X k = A X k − 1 + B U k − 1 X_{k}=A X_{k-1}+B U_{k-1} Xk=AXk−1+BUk−1 这个公式得到的 X ^ k \hat{X}_{k} X^k 其实是不正确的,在这里在上面增加一个小小的负号, 表明它是先验估计值。
  X ^ k − = A X ^ k − 1 + B U k − 1 , ( 这里的 X ^ k − 1 也是估计值 ) \hat{X}_{k}^{-}=A \widehat{X}_{k-1}+B U_{k-1} , (这里的 \widehat{X}_{k-1} 也是估计值) X^k−=AX k−1+BUk−1,(这里的X k−1也是估计值)
  由于我们是知道测试结果(测量得到) Z k , Z_{k} , Zk,
  那么在不考虑测量噪音的情况下, 可以大体得到一个估计的 X ^ k \hat{X}_{k} X^k ,
  那么我们令这个估计的 X ^ k 命名为 X ^ k m \hat{X}_{k} 命名为 \hat{X}_{k_{m}} X^k命名为X^km ，表示这是根据测试结果估计得到的 X ^ k \hat{X}_{k} X^k
  那么, 根据公式 Z k = H X ^ k Z_{k}=H \hat{X}_{k} Zk=HX^k , 可以得到
  X ^ k mea = H − 1 Z k , ( 由于是可以观测的系统 , 因此 H 一定是可逆的 ) \hat{X}_{k_{\text {mea }}}=H^{-1} Z_{k} , (由于是可以观测的系统, 因此 \mathrm{H} 一定是可逆的) X^kmea =H−1Zk,(由于是可以观测的系统,因此H一定是可逆的)
  因此我们得到了两个不同的关于Xk的结果，一个是先验结果xk-（算出来的），另一个是测出来的结果xkmca（测出来的），但是着两个其实都是不准确的，因为其没有考虑噪声的影响我们真正要求的是xk（表示后验），包含了噪声的影响。
  引入数据融合的概念
  结合数据融合的概念可以得到
  已知 X ^ k − , X ^ k mea 那么 X ^ k = X ^ k − + G ( X ^ k mea − X ^ k − ) , ( G 是方阵也就是要推导和卡尔曼增益 ) 已知 \hat{X}_{k}{ }^{-}, \hat{X}_{k_{\text {mea }}} 那么 \hat{X}_{k}=\hat{X}_{k}^{-}+G\left(\hat{X}_{k_{\text {mea }}}-\hat{X}_{k}^{-}\right),(\mathrm{G} 是方阵也就是要推导和卡尔曼增益 ) 已知X^k−,X^kmea 那么X^k=X^k−+G(X^kmea −X^k−),(G是方阵也就是要推导和卡尔曼增益)
  X ^ k mea = H − 1 Z k , 那么 X ^ k = X ^ k − + G ( H − 1 Z k − X ^ k − ) , 那么令 K k = G H − 1 , 便可以得到 X ^ k = X ^ k − + K k ( Z k − H X ^ k − ) , 那么在此时 K k ∉ ( 0 , 1 ) , 而是 K k ∉ ( 0 , H − 1 ) , \hat{X}_{k_{\text {mea }}}=H^{-1} Z_{k} , 那么 \hat{X}_{k}=\hat{X}_{k}^{-}+G\left(H^{-1} Z_{k}-\widehat{X}_{k}^{-}\right) , 那么令 K_{k}=G H^{-1} , 便可以得到 \hat{X}_{k}=\hat{X}_{k}^{-}+K_{k}\left(Z_{k}-H \hat{X}_{k}{ }^{-}\right) , 那么在此时 K_{k} \notin(0,1) , 而是 K_{k} \notin\left(0, H^{-1}\right) , X^kmea =H−1Zk,那么X^k=X^k−+G(H−1Zk−X k−),那么令Kk=GH−1,便可以得到X^k=X^k−+Kk(Zk−HX^k−),那么在此时Kk∈/(0,1),而是Kk∈/(0,H−1),
  推导卡尔曼增益
  因此我们的目标就变得十分清晰了，就是求使得考虑了噪声之后的估计值趋近于真实值,
  那么此时引入误差： e k = X k − X ^ k e_{k}=X_{k}-\hat{X}_{k} ek=Xk−X^k
  同理P ( e k ) ∼ ( 0 , P ) , P 也是那个协方差矩阵 \text { 同理P }\left(e_{k}\right) \sim(0, P), P \text { 也是那个协方差矩阵 } 同理P (ek)∼(0,P),P 也是那个协方差矩阵
  而当在不同的维度上的方差越小，那么说明这个e越接近0，因此估计值和真实值也就是最相近的。所以，要选择合适的K使得tr（P）（矩阵对角线相加)最小，那么优化问题就变成了下面这个公式。
  P = E ( e k e k T ) = E ( ( X k − X ^ k ) ( X k − X ^ k ) T ) , 将 X ^ k = X ^ k − + K k ( Z k − H X ^ k − ) 代入, 可以得到 P = E ( ( X k − ( X ^ k − + K k ( Z k − H X ^ k − ) ) ) ( X k − ( X ^ k − + K k ( Z k − H X ^ k − ) ) ) T ) , \begin{array}{l} \mathrm{P}=\mathrm{E}\left(e_{k} e_{k}{ }^{T}\right)=\mathrm{E}\left(\left(X_{k}-\hat{X}_{k}\right)\left(X_{k}-\hat{X}_{k}\right)^{T}\right), \\ \text { 将 } \hat{X}_{k}=\hat{X}_{k}^{-}+K_{k}\left(Z_{k}-H \hat{X}_{k}^{-}\right) \text {代入, } \\ \text { 可以得到 } \mathrm{P}=\mathrm{E}\left(\left(X_{k}-\left(\hat{X}_{k}^{-}+K_{k}\left(Z_{k}-H \hat{X}_{k}^{-}\right)\right)\right)\left(X_{k}-\left(\hat{X}_{k}^{-}+K_{k}\left(Z_{k}-H \hat{X}_{k}^{-}\right)\right)\right)^{T}\right) \text {, } \\ \end{array} P=E(ekekT)=E((Xk−X^k)(Xk−X^k)T), 将 X^k=X^k−+Kk(Zk−HX^k−)代入, 可以得到 P=E((Xk−(X^k−+Kk(Zk−HX^k−)))(Xk−(X^k−+Kk(Zk−HX^k−)))T),
  那么此时将 Z k = H X k + v k , 进行替换。那么此时将 Z_{k}=H X_{k}+v_{k} , 进行替换。那么此时将Zk=HXk+vk,进行替换。
  那么 X k − X ^ k = X k − X ^ k − − K k X_{k}-\hat{X}_{k}=X_{k}-\hat{X}_{k}^{-}-K_{k} Xk−X^k=Xk−X^k−−Kk ( H X k + v k ) + K k H X ^ k − = X k − X ^ k − − K k \left(H X_{k}+v_{k}\right)+K_{k} H \hat{X}_{k}^{-}=X_{k}-\hat{X}_{k}^{-}-K_{k} (HXk+vk)+KkHX^k−=Xk−X^k−−Kk
  H ( X k − X ^ k − ) − K k v k = ( I − K k H ) ( X k − X ^ k − ) − K k v k , H\left(X_{k}-\hat{X}_{k}^{-}\right)-K_{k} v_{k}=\left(I-K_{k} H\right)\left(X_{k}-\hat{X}_{k}^{-}\right)-K_{k} v_{k} , H(Xk−X^k−)−Kkvk=(I−KkH)(Xk−X^k−)−Kkvk,
  由于 e k = X k − X ^ k e_{k}=X_{k}-\widehat{X}_{k} ek=Xk−X k , 因此也可以命名 X k − X ^ k − 为 e k X_{k}-\widehat{X}_{k}^{-} 为 e_{k} Xk−X k−为ek 的先验, 记为 e k − , e_{k}{ }^{-} , ek−,
  因此 P 可改写: P = E ( e k e k T ) = E ( ( ( I − K k H ) e k − − K k v k ) ( ( I − K k H ) e k − − K k v k ) T ) , \text { 因此 } \mathrm{P} \text { 可改写:} \mathrm{P}=\mathrm{E}\left(e_{k} e_{k}{ }^{T}\right)=\mathrm{E}\left(\left(\left(I-K_{k} H\right) e_{k}{ }^{-}-K_{k} v_{k}\right)\left(\left(I-K_{k} H\right) e_{k}^{-}-K_{k} v_{k}\right)^{T}\right) \text {, } 因此 P 可改写:P=E(ekekT)=E(((I−KkH)ek−−Kkvk)((I−KkH)ek−−Kkvk)T),
  = E [ ( I − k k H ) e k ′ e k T T ( I − k k H ) T − ( I − k k H ) e k ′ v k T k k T − k k v k e k r T ( I − k k H ) T + k k v k v k T k k T ] = E [ ( I − k k H ) e k ′ e k ′ T ( I − k k H ) T ] − E [ ( I − k k H ) e k ′ v k T k k T ] − E [ k k v k e k ′ T ( I − k k H ) T ] + E [ k k v k v k T k k T ] \begin{array}{c} =\mathrm{E}\left[\left(I-k_{k} H\right) e_{k}^{\prime} e_{k}^{T T}\left(I-k_{k} H\right)^{T}-\left(I-k_{k} H\right) e_{k}^{\prime} v_{k}{ }^{T} k_{k}{ }^{T}-k_{k} v_{k} e_{k}^{r T}\left(I-k_{k} H\right)^{T}+k_{k} v_{k} v_{k}{ }^{T} k_{k}{ }^{T}\right] \\ =\mathrm{E}\left[\left(I-k_{k} H\right) e_{k}^{\prime} e_{k}^{\prime T}\left(I-k_{k} H\right)^{T}\right]-E\left[\left(I-k_{k} H\right) e_{k}^{\prime} v_{k}{ }^{T} k_{k}{ }^{T}\right]-E\left[k_{k} v_{k} e_{k}^{\prime T}\left(I-k_{k} H\right)^{T}\right] \\ +E\left[k_{k} v_{k} v_{k}{ }^{T} k_{k}{ }^{T}\right] \end{array} =E[(I−kkH)ek′ekTT(I−kkH)T−(I−kkH)ek′vkTkkT−kkvkekrT(I−kkH)T+kkvkvkTkkT]=E[(I−kkH)ek′ek′T(I−kkH)T]−E[(I−kkH)ek′vkTkkT]−E[kkvkek′T(I−kkH)T]+E[kkvkvkTkkT]
  因为 E [ e k − ] = 0 , E [ v k T ] = 0 上式可简化为 : = E [ ( I − k k H ) e k ′ e k T T ( I − k k H ) T ] + E [ k k v k v k T k k T ] = ( I − k k H ) E [ e k ′ e k T T ] ( I − k k H ) T + k k E [ v k v k T ] k k T 设 P k − = E [ e k ′ e k ′ T ] , R = E [ v k v k T ] , 于是有 : = ( I − k k H ) P k ′ ( I − k k H ) T + k k R k k T = ( P k ′ − k k H P k ′ ) ( I − k k H ) T + k k R k k T = ( P k ′ − k k H P k ′ ) ( I T − H T k k T ) + k k R k k T P k = P k ′ − k k H P k ′ − P k ′ H T k k T + k k H P k ′ H T k k T + k k R k k T 因为 P k ′ H T k k T = ( k k ( P k ′ H T ) ) T = ( k k H P k ′ T ) T tr ⁡ ( P k ) = tr ⁡ ( P k ′ ) − 2 tr ⁡ ( k k H P k ′ ) + tr ⁡ ( k k H P k ′ H T k k T ) + tr ⁡ ( k k R k k T ) 令 dtr ⁡ ( P k ) d k k = 0 又因为 : d t r ( A B ) d A = B T dtr ⁡ ( A B A T ) d A = A B + A B T 因为 R 、 H P k − H T 是对角矩阵 , 所以 : tr ⁡ ( k k H P k ′ H T k k T ) = 2 k k H P k ′ H T , tr ⁡ ( k k R k k T ) = 2 k k R 于是有。因为 \mathrm{E}\left[e_{k}^{-}\right]=0, E\left[v_{k}{ }^{T}\right]=0 上式可简化为: \begin{array}{l} =\mathrm{E}\left[\left(I-k_{k} H\right) e_{k}^{\prime} e_{k}^{T T}\left(I-k_{k} H\right)^{T}\right]+E\left[k_{k} v_{k} v_{k}{ }^{T} k_{k}{ }^{T}\right] \\ =\left(I-k_{k} H\right) \mathrm{E}\left[e_{k}^{\prime} e_{k}{ }^{T T}\right]\left(I-k_{k} H\right)^{T}+k_{k} E\left[v_{k} v_{k}{ }^{T}\right] k_{k}{ }^{T} \end{array} 设 P_{k}^{-}=\mathrm{E}\left[e_{k}^{\prime} e_{k}^{\prime T}\right], R=E\left[v_{k} v_{k}{ }^{T}\right] ,于是有: \begin{array}{c} =\left(I-k_{k} H\right) P_{k}^{\prime}\left(I-k_{k} H\right)^{T}+k_{k} R k_{k}{ }^{T} \\ =\left(P_{k}^{\prime}-k_{k} H P_{k}^{\prime}\right)\left(I-k_{k} H\right)^{T}+k_{k} R k_{k}{ }^{T} \\ =\left(P_{k}^{\prime}-k_{k} H P_{k}^{\prime}\right)\left(I^{T}-H^{T} k_{k}{ }^{T}\right)+k_{k} R k_{k}{ }^{T} \\ \mathrm{P}_{k}=P_{k}^{\prime}-k_{k} H P_{k}^{\prime}-P_{k}^{\prime} H^{T} k_{k}{ }^{T}+k_{k} H P_{k}^{\prime} H^{T} k_{k}{ }^{T}+k_{k} R k_{k}{ }^{T} \end{array} 因为 P_{k}^{\prime} H^{T} k_{k}{ }^{T}=\left(k_{k}\left(P_{k}^{\prime} H^{T}\right)\right)^{T}=\left(k_{k} H P_{k}^{\prime T}\right)^{T} \operatorname{tr}\left(\mathrm{P}_{k}\right)=\operatorname{tr}\left(P_{k}^{\prime}\right)-2 \operatorname{tr}\left(k_{k} H P_{k}^{\prime}\right)+\operatorname{tr}\left(k_{k} H P_{k}^{\prime} H^{T} k_{k}{ }^{T}\right)+\operatorname{tr}\left(k_{k} R k_{k}{ }^{T}\right) 令 \frac{\operatorname{dtr}\left(\mathrm{P}_{k}\right)}{d k_{k}}=0 又因为: \begin{array}{c} \frac{\mathrm{dtr}(\mathrm{AB})}{d A}=B^{T} \\ \frac{\operatorname{dtr}\left(\mathrm{ABA}^{T}\right)}{d A}=A B+\mathrm{AB}^{T} \end{array} 因为 \mathrm{R} 、 H P_{k}^{-} H^{T} 是对角矩阵, 所以: \operatorname{tr}\left(k_{k} H P_{k}^{\prime} H^{T} k_{k}^{T}\right)=2 k_{k} H P_{k}^{\prime} H^{T}, \quad \operatorname{tr}\left(k_{k} R k_{k}^{T}\right)=2 k_{k} R 于是有。因为E[ek−]=0,E[vkT]=0上式可简化为:=E[(I−kkH)ek′ekTT(I−kkH)T]+E[kkvkvkTkkT]=(I−kkH)E[ek′ekTT](I−kkH)T+kkE[vkvkT]kkT设Pk−=E[ek′ek′T],R=E[vkvkT],于是有:=(I−kkH)Pk′(I−kkH)T+kkRkkT=(Pk′−kkHPk′)(I−kkH)T+kkRkkT=(Pk′−kkHPk′)(IT−HTkkT)+kkRkkTPk=Pk′−kkHPk′−Pk′HTkkT+kkHPk′HTkkT+kkRkkT因为Pk′HTkkT=(kk(Pk′HT))T=(kkHPk′T)Ttr(Pk)=tr(Pk′)−2tr(kkHPk′)+tr(kkHPk′HTkkT)+tr(kkRkkT)令dkkdtr(Pk)=0又因为:dAdtr(AB)=BTdAdtr(ABAT)=AB+ABT因为R、HPk−HT是对角矩阵,所以:tr(kkHPk′HTkkT)=2kkHPk′HT,tr(kkRkkT)=2kkR于是有。
  − P k ′ H T + k k ( H P k ′ H T + R ) = 0 k k ( H P k ′ H T + R ) = P k ′ H T k k = P k ′ H T H P k ′ H T + R \begin{array}{c} -P_{k}^{\prime} H^{T}+k_{k}\left(H P_{k}^{\prime} H^{T}+R\right)=0 \\ k_{k}\left(H P_{k}^{\prime} H^{T}+R\right)=P_{k}^{\prime} H^{T} \\ k_{k}=\frac{P_{k}^{\prime} H^{T}}{H P_{k}^{\prime} H^{T}+R} \end{array} −Pk′HT+kk(HPk′HT+R)=0kk(HPk′HT+R)=Pk′HTkk=HPk′HT+RPk′HT