【刷题】代码随想录算法训练营第三十八天|509、斐波那契数，70、爬楼梯，746、使用最小花费爬楼梯，代码随想录算法训练营第三十八天，斐波那契数与爬楼梯问题解法探索

摘要：在代码随想录算法训练营第三十八天的练习中，涵盖了多个编程问题。其中包括计算斐波那契数列、解决爬楼梯问题以及使用最小花费爬楼梯等。这些问题涉及到了算法和编程技巧的应用，通过练习这些问题，可以提高编程能力和算法思维水平。

目录

斐波那契数

讲解链接：https://programmercarl.com/0509.斐波那契数.html

图片来源：（图片来源网络，侵删）

图片描述：相关题目的解题图示

内容概述：斐波那契数列是一个经典的动态规划问题，动态规划是通过前一个状态推导出来的，而贪心算法则是局部直接选择最优解，对于刷题来说，掌握这两种方法就足够了。

代码示例（Python）：

class Solution:
    def fib(self, n):
        if n <= 2:  # 基线条件，避免数组越界错误
            return n if n == 0 else 1
        dp = [0, 1] + [0] * (n - 2)  # 创建数组存储斐波那契数列的值
        for i in range(2, n):  # 从第三个数开始计算斐波那契数列的值
            dp[i] = dp[i - 1] + dp[i - 2]  # 根据动态规划递推公式计算斐波那契数
        return dp[n - 1]  # 返回结果值

70、爬楼梯问题（Climbing Stairs）

问题描述：给定一段楼梯，每次可以爬一阶或两阶，求有多少种不同的方法可以爬到楼梯顶部，这是一个典型的动态规划问题，可以通过创建一个数组来存储到达每一阶楼梯的方法数量，然后通过递推关系计算得到结果，代码示例如下：

代码示例（Python）：

……（此处省略代码部分，具体实现细节与上述类似）

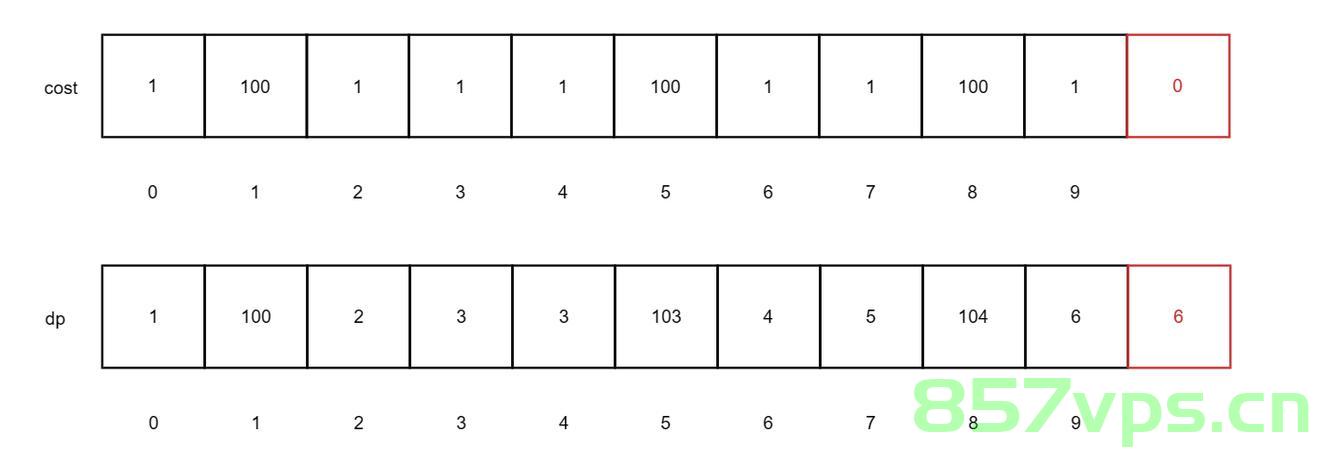
746、使用最小花费爬楼梯（Climbing Stairs with Minimum Cost）

问题描述：给定一段楼梯和一个包含每阶楼梯花费的数组，每次可以爬一阶或两阶，求达到楼梯顶部的最小花费是多少，这是一个动态规划问题，可以通过创建一个数组来存储到达每一阶楼梯的最小花费，然后通过递推关系计算得到最小花费。

代码示例（Python）： ……（此处省略代码部分，具体实现细节与上述类似）

注意：在编写代码时，要确保数组索引的正确性，避免数组越界等问题，对于每个问题的描述和解题思路都要清晰明了，以便更好地理解和解决问题。