第十四届蓝桥杯省赛真题 Java 研究生 组【原卷】，第十四届蓝桥杯省赛Java研究生组真题原卷解析

温馨提示：这篇文章已超过468天没有更新，请注意相关的内容是否还可用！

这是第十四届蓝桥杯省赛Java研究生组的真题原卷摘要。该比赛旨在考察研究生在Java编程领域的实力和技能。试题内容涵盖算法设计、数据结构、面向对象编程等多个方面，旨在检验参赛者的编程思维、问题解决能力和创新能力。这份真题对于准备参加类似比赛的学生和开发者来说，具有很高的参考价值和指导意义。

文章目录

发现宝藏
【考生须知】
试题 A: 特殊日期
试题 B: 与或异或
试题 C: 棋盘
试题 D: 子矩阵
试题 E : \mathrm{E}: E: 互质数的个数
试题 F: 小蓝的旅行计划
试题 G: 奇怪的数
试题 H: 太阳
试题 I: 高塔
试题 J \mathrm{J} J : 反异或 01 串
发现宝藏
前些天发现了一个巨牛的人工智能学习网站，通俗易懂，风趣幽默，忍不住分享一下给大家。【宝藏入口】。
第十四届蓝桥杯大赛软件赛省赛 Java 研究生组
【考生须知】
考试开始后, 选手首先下载题目, 并使用考场现场公布的解压密码解压试题。
考试时间为 4 小时。考试期间选手可浏览自己已经提交的答案, 被浏览的答案允许拷贝。时间截止后，将无法继续提交或浏览答案。
对同一题目, 选手可多次提交答案, 以最后一次提交的答案为准。
选手必须通过浏览器方式提交自己的答案。选手在其它位置的作答或其它方式提交的答案无效。
试题包含 “结果填空” 和 “程序设计” 两种题型。
结果填空题: 要求选手根据题目描述直接填写结果。求解方式不限。不要求源代码。把结果填空的答案直接通过网页提交即可, 不要书写多余的内容。
程序设计题: 要求选手设计的程序对于给定的输入能给出正确的输出结果。考生的程序只有能运行出正确结果才有机会得分。
注意: 在评卷时使用的输入数据与试卷中给出的示例数据可能是不同的。选手的程序必须是通用的, 不能只对试卷中给定的数据有效。
所有源码必须在同一文件中。调试通过后，拷贝提交。
注意: 不要使用 package 语句。
注意：选手代码的主类名必须为: Main, 否则会被判为无效代码。
注意: 如果程序中引用了类库, 在提交时必须将 import 语句与程序的其他部分同时提交。只允许使用 Java 自带的类库。
试题 A: 特殊日期
本题总分: 5 分
【问题描述】
记一个日期为 y y y y yy 年 m m m m mm 月 d d d d dd 日, 统计从 2000 年 1 月 1 日 (含) 到 2000000 年 1 月 1 日 (含), 有多少个日期满足年份 y y y y yy 是月份 m m m m mm 的倍数, 同时也是 d d d d dd 的倍数。
当年份是 4 的倍数而不是 100 的倍数或者年份是 400 的倍数时, 这一年是闰年，其他的年份都不是闰年。
【答案提交】
这是一道结果填空的题, 你只需要算出结果后提交即可。本题的结果为一个整数, 在提交答案时只填写这个整数, 填写多余的内容将无法得分。
试题 B: 与或异或
本题总分: 5 分
【问题描述】
小蓝有一张门电路的逻辑图, 如下图所示:
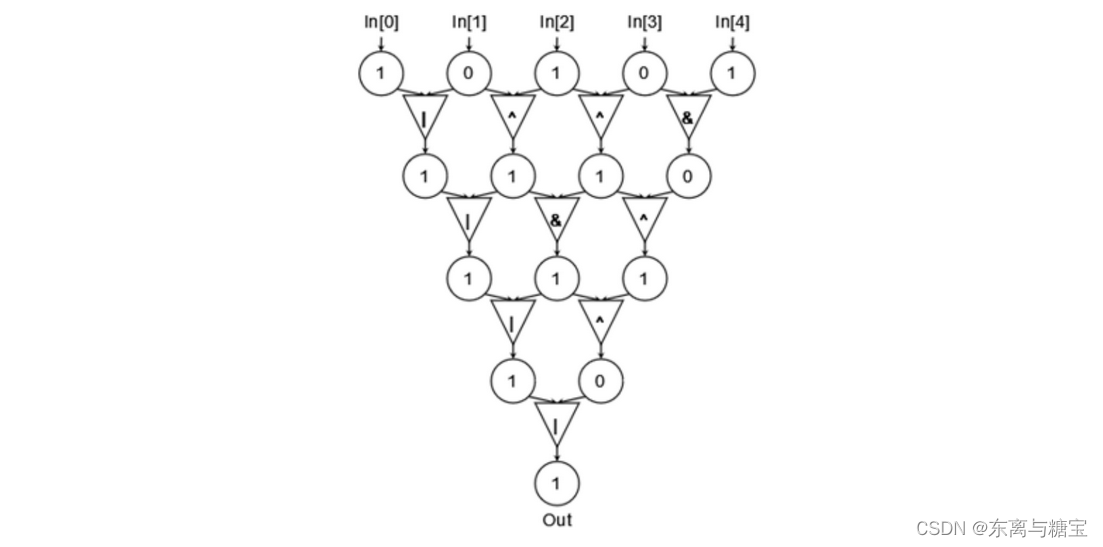
图中每个三角形代表着一种门电路, 可能是与门、或门、异或门中的任何一种, 它接受上一层中的两个圆形中的数据作为输入, 产生一个输出值输出到下一级 (如图中箭头所示)。图中圆形表示的是暂存的输出结果, 取值只可能是 0 或 1 , 为了便于表示我们用 arr ⁡ [ i ] [ j ] \operatorname{arr}[i][j] arr[i][j] 表示第 i ( 0 ≤ i ≤ 4 ) i(0 \leq i \leq 4) i(0≤i≤4) 行第 j ( 0 ≤ j ≤ i ) j(0 \leq j \leq i) j(0≤j≤i) 个圆形的值。其中 arr ⁡ [ 0 ] = ( In ⁡ [ 0 ] , In ⁡ [ 1 ] , In ⁡ [ 2 ] , In ⁡ [ 3 ] , In ⁡ [ 4 ] ) \operatorname{arr}[0]=(\operatorname{In}[0], \operatorname{In}[1], \operatorname{In}[2], \operatorname{In}[3], \operatorname{In}[4]) arr[0]=(In[0],In[1],In[2],In[3],In[4]) 表示的是输入数据, 对于某个 arr ⁡ [ i ] [ j ] ( i ≤ 0 ) \operatorname{arr}[i][j](i \leq 0) arr[i][j](i≤0), 计算方式为 arr ⁡ [ i ] [ j ] = arr ⁡ [ i − 1 ] [ j ] op ⁡ arr ⁡ [ i − 1 ] [ j + 1 ] \operatorname{arr}[i][j]=\operatorname{arr}[i-1][j] \operatorname{op} \operatorname{arr}[i-1][j+1] arr[i][j]=arr[i−1][j]oparr[i−1][j+1], 其中 o p o p op 表示的是将 arr ⁡ [ i − 1 ] [ j ] 、 arr ⁡ [ i − 1 ] [ j + 1 ] \operatorname{arr}[i-1][j] 、 \operatorname{arr}[i-1][j+1] arr[i−1][j]、arr[i−1][j+1] 作为输入, 将 arr ⁡ [ i ] [ j ] \operatorname{arr}[i][j] arr[i][j] 作为输出的那个门电路, 与门、或门、异或门分别对应于按位与 (&)、按位或 (I)、按位异或 (^) 运算符。
现在已知输入为 In ⁡ [ 0 ] = 1 , In ⁡ [ 1 ] = 0 , In ⁡ [ 2 ] = 1 , In ⁡ [ 3 ] = 0 , In ⁡ [ 4 ] = 1 \operatorname{In}[0]=1, \operatorname{In}[1]=0, \operatorname{In}[2]=1, \operatorname{In}[3]=0, \operatorname{In}[4]=1 In[0]=1,In[1]=0,In[2]=1,In[3]=0,In[4]=1, 小蓝想要使得最终的输出 Out 的值为 1, 请问一共有多少种不同的门电路组合方式?其中上图中显示的就是一种合法的方式。
【答案提交】
这是一道结果填空的题, 你只需要算出结果后提交即可。本题的结果为一个整数, 在提交答案时只填写这个整数, 填写多余的内容将无法得分。
试题 C: 棋盘
时间限制: 3.0 s 3.0 \mathrm{~s} 3.0 s 内存限制: 512.0 M B 512.0 \mathrm{MB} 512.0MB 本题总分: 10 分
【问题描述】
小蓝拥有 n × n n \times n n×n 大小的棋盘, 一开始棋盘上全都是白子。小蓝进行了 m m m 次操作, 每次操作会将棋盘上某个范围内的所有棋子的颜色取反 (也就是白色棋子变为黑色, 黑色棋子变为白色)。请输出所有操作做完后棋盘上每个棋子的颜色。
【输入格式】
输入的第一行包含两个整数 n , m n, m n,m, 用一个空格分隔, 表示棋盘大小与操作数。
接下来 m m m 行每行包含四个整数 x 1 , y 1 , x 2 , y 2 x_{1}, y_{1}, x_{2}, y_{2} x1,y1,x2,y2, 相邻整数之间使用一个空格分隔, 表示将在 x 1 x_{1} x1 至 x 2 x_{2} x2 行和 y 1 y_{1} y1 至 y 2 y_{2} y2 列中的棋子颜色取反。
【输出格式】
输出 n n n 行, 每行 n n n 个 0 或 1 表示该位置棋子的颜色。如果是白色则输出 0 , 否则输出 1 。
【样例输入】
3 3 \begin{array}{llll}3 &3\end{array} 33
1 1 2 2 \begin{array}{llll}1 & 1 & 2 & 2\end{array} 1122
2 2 3 3 \begin{array}{llll}2 & 2 & 3 & 3\end{array} 2233
1 1 3 3 \begin{array}{llll}1 & 1 & 3 & 3\end{array} 1133
【样例输出】
【评测用例规模与约定】
对于 30 % 30 \% 30% 的评测用例, n m ≤ 500 n \mathrm{~m} \leq 500 n m≤500 ；
对于所有评测用例， 1 ≤ n , m ≤ 2000 , 1 ≤ x 1 ≤ x 2 ≤ n , 1 ≤ y 1 ≤ y 2 ≤ m 1 \leq n, m \leq 2000,1 \leq x_{1} \leq x_{2} \leq n, 1 \leq y_{1} \leq y_{2} \leq m 1≤n,m≤2000,1≤x1≤x2≤n,1≤y1≤y2≤m 。
试题 D: 子矩阵
时间限制: 5.0 s 5.0 \mathrm{~s} 5.0 s 内存限制: 512.0 M B 512.0 \mathrm{MB} 512.0MB 本题总分: 10 分
【问题描述】
给定一个 n × m n \times m n×m ( n n n 行 m m m 列 ) ) ) 的矩阵。
设一个矩阵的价值为其所有数中的最大值和最小值的乘积。求给定矩阵的所有大小为 a × b a \times b a×b ( a a a 行 b b b 列 ) ) ) 的子矩阵的价值的和。
答案可能很大, 你只需要输出答案对 998244353 取模后的结果。
【输入格式】
输入的第一行包含四个整数分别表示 n , m , a , b n, m, a, b n,m,a,b, 相邻整数之间使用一个空格分隔。
接下来 n n n 行每行包含 m m m 个整数, 相邻整数之间使用一个空格分隔, 表示矩阵中的每个数 A i , j A_{i, j} Ai,j 。
【输出格式】
输出一行包含一个整数表示答案。
【样例输入】
2 3 1 2 \begin{array}{llll}2 & 3 & 1 & 2\end{array} 2312
1 2 3 \begin{array}{lll}1 & 2 & 3\end{array} 123
4 5 6 \begin{array}{lll}4& 5& 6\end{array} 456
【样例输出】
58 \begin{array}{lll}58\end{array} 58
【样例说明】
1 × 2 + 2 × 3 + 4 × 5 + 5 × 6 = 58 1 \times 2+2 \times 3+4 \times 5+5 \times 6=58 1×2+2×3+4×5+5×6=58 。
【评测用例规模与约定】
对于 40 % 40 \% 40% 的评测用例， 1 ≤ n , m ≤ 100 1 \leq n, m \leq 100 1≤n,m≤100 ；
对于 70 % 70 \% 70% 的评测用例， 1 ≤ n , m ≤ 500 1 \leq n, m \leq 500 1≤n,m≤500 ；
对于所有评测用例， 1 ≤ a ≤ n ≤ 10001 ≤ b ≤ m ≤ 10001 ≤ A i , j ≤ 1 0 9 1 \leq a \leq n \leq 10001 \leq b \leq m \leq 10001 \leq A_{i, j} \leq 10^{9} 1≤a≤n≤10001≤b≤m≤10001≤Ai,j≤109 。
试题 E : \mathrm{E}: E: 互质数的个数
时间限制: 3.0 s 3.0 \mathrm{~s} 3.0 s 内存限制: 512.0MB 本题总分: 15 分
【问题描述】
给定 a , b a, b a,b, 求 1 ≤ x