差分算法及模板详解，差分算法详解及模板介绍，差分算法详解及模板介绍指南

摘要：本文介绍了差分算法及其模板的详细解析。差分算法是一种数值计算方法，通过计算数据点的差值来求解近似解。本文详细阐述了差分算法的原理、应用和优点，并提供了差分算法的模板介绍，帮助读者更好地理解和应用差分算法。通过本文的阅读，读者可以更加深入地了解差分算法，并能够在实践中灵活运用。

差分算法是一种数值计算方法，用于求解微分方程的近似解，差分算法的核心思想是通过构造差分数组来简化运算，特别是对于区间操作，可以大大降低时间复杂度，下面详细介绍一维差分算法的原理、步骤和应用，并给出代码模板。

差分算法原理

差分思想和前缀和是相反的，我们定义一个数组a，其中a[1]、a[2]...a[n]表示前缀和，为了表示a数组的变化量，我们构造一个差分数组b，通过差分数组的前缀和来表示a数组的值，a[n]等于差分数组的前缀和。

差分算法步骤

1、初始化数组a和差分数组b，全部赋值为0。

2、输入a数组的值。

3、构造差分数组b，其中b[1]等于a[1]，b[i]（i大于等于2）等于a[i]减去a[i-1]。

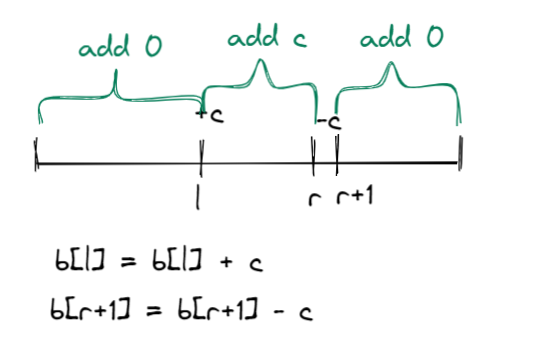
4、对于每个操作，给定一个区间[l,r]和一个常数c，调整差分数组的两个边界值，使得区间内的每个数都加上c。

5、通过差分数组的前缀和计算得到最终的a数组。

应用与代码模板

下面是一个简单的例子，输入一个长度为n的整数序列，然后进行m次操作，每次操作将序列中某个区间内的数加上一个常数c，下面是代码模板：

#include <iostream>
using namespace std;
const int N = 100010; // 定义常量N为数组的最大长度
int a[N], b[N]; // 定义数组a和差分数组b
int main() {
    int n, m; // 定义变量n和m分别表示整数序列的长度和操作次数
    cin >> n >> m; // 输入整数序列的长度和操作次数
    for (int i = 1; i <= n; i++) { // 输入整数序列的值并初始化差分数组b为全零数组
        cin >> a[i]; // 输入整数序列的值到数组a中
        b[i] = a[i] - a[i - 1]; // 计算差分数组b的值并初始化第一个元素为原序列的第一个元素值（因为前缀和为原序列的第一个元素）
    }
    for (int i = 0; i < m; i++) { // 处理m个操作
        int l, r, c; // 定义变量l、r和c分别表示操作的区间和增加的常数c的值
        cin >> l >> r >> c; // 输入操作的区间和增加的常数c的值到变量l、r和c中
        b[l] += c; // 在差分数组中将区间左端点的值增加常数c的值（表示在左端点处增加c的值）
        if (r + 1 <= n) b[r + 1] -= c; // 在差分数组中将区间右端点下一个位置的值减去常数c的值（表示在右端点处抵消之前增加的值）以保持原始序列不变性（注意下标加一并检查是否越界）
    }
    // 计算最终序列的值并输出到控制台窗口上（具体实现细节需要根据题目要求编写完成）
    return 0; // 程序正常结束并返回结果到控制台窗口上（此处省略了计算最终序列的代码部分）的具体实现细节需要根据题目要求编写完成并输出最终结果到控制台窗口上，在实际编写代码时需要注意处理边界条件和特殊情况以避免出现错误或异常行为，关于二维差分的内容可以通过扩展一维差分的思路来处理二维区间操作的问题，希望这些信息对您有所帮助！如果您还有其他问题或需要进一步的帮助请随时向我提问我会尽力为您提供帮助和支持谢谢！祝您编程愉快！加油！保持耐心！坚持就是胜利！加油！加油！加油！加油！加油！加油！加油！加油！加油！加油！加油！加油！加油！加油！加油！加油！加油！）