“回文子串、最长回文子序列”总结，动态规划再显神通（Java实现），动态规划解析，回文子串与最长回文子序列的Java实现总结

摘要：本文介绍了回文子串和最长回文子序列的概念，并通过动态规划的方法实现了Java代码。动态规划在处理这类问题时展现出其独特的优势，能够高效地解决寻找回文序列的问题。通过动态规划算法，能够在时间复杂度较低的情况下找到最长的回文子序列。本文提供了相关知识的概述和Java实现的简要思路。

一、回文子串

题目描述：

给定一个字符串，你的任务是计算这个字符串中有多少个回文子串，回文串是指正着读和倒着读一样的字符串。

“abcba”就是一个回文串。

题目来源： 647. 回文子串

1、dp定义

分析：

对于这类问题，如果我们继续采用传统的定义方式（如“以字符串第i个元素为结尾...”），可能会难以找到状态转移的规律，考虑到回文子串的特性，我们可以定义一个二维的dp数组，用来表示字符串的区间[i, j]是否是回文。

dp定义：

dp[i][j]（布尔类型）：区间[i, j]是否为回文子串，当dp[i][j]为True时，表示从第i个字符到第j个字符（包括两端）组成的子串是回文串。

2、递推公式

分析：

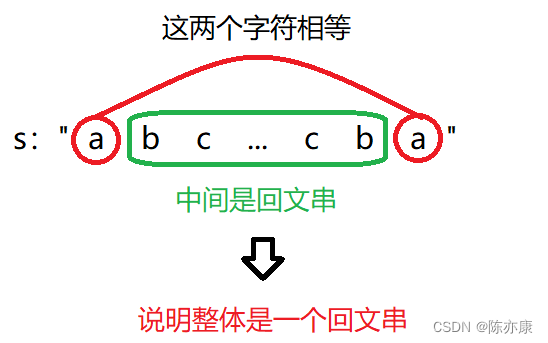
根据回文串的性质，我们可以得出以下结论：如果一个字符串的左右两端的字符相同，并且除了这两个字符外的中间部分是一个回文串，那么这个字符串整体就是一个回文串，当区间长度小于等于1时，任何字符串都是回文串，基于这些性质，我们可以得出状态转移方程。

状态转移方程：

s.charAt(i) == s.charAt(j)，即左右两端字符相等，那么有以下两种情况：

- 当 j - i <= 1 时（即区间长度小于等于1），区间一定是回文的，dp[i][j] = true。

- 当 j - i > 1 时，我们需要检查去掉两端字符后的子串（即区间 [i+1, j-1]）是否为回文串，如果是，那么加上两端的字符就形成了一个新的回文串，dp[i][j] = true，否则，dp[i][j] = false，我们需要遍历所有可能的区间长度和起始位置来检查这些条件，具体的解题代码将在后续部分给出。

for (int len = 2; len <= s.length(); len++) { //遍历所有可能的子串长度
    for (int i = 0; i <= s.length() - len; i++) { //遍历所有可能的起始位置
        int j = i + len - 1; //计算对应的结束位置
        if (s.charAt(i) == s.charAt(j) && (len <= 2 || dp[i+1][j-1])) { //如果两端字符相等且去掉两端后的子串是回文的，则当前子串是回文的
            dp[i][j] = true; //标记为回文子串
        } else { //否则不是回文子串，不需要进行任何操作或标记（保持默认值false）} } } } } } } } } } } } } } } } } } } } } } } } } } }} ```注意： 上述代码仅为状态转移方程的描述性表示，并非实际代码实现，在实际编程中，我们需要考虑边界条件、初始化等问题，具体的解题代码将在后续部分给出，由于题目要求计算的是所有回文子串的数量而非判断是否为回文子串本身，我们还需要使用一个变量来累加符合条件的区间数量，这样最终得到的答案就是所有符合条件的回文子串的数量。