归并排序算法C++实现（超详细解析！！！！），C++归并排序算法的超详细解析与实现

摘要：本文介绍了归并排序算法的C++实现，并提供了详细的解析。该算法采用分治法的思想，将待排序序列不断分割成子序列，直到子序列有序，然后将有序子序列合并成最终的有序序列。文章详细阐述了归并排序算法的实现过程，包括递归实现和合并操作的具体细节，帮助读者更好地理解和掌握归并排序算法的核心思想。

目录

（1）分治算法

分治算法是一种解决问题的策略，即将一个大规模的问题分解为若干个规模较小的相同子问题，通过分而治之的方式逐一解决，在算法设计中，我们引入这种策略。

（2）分治算法解题方法

1、分解：将待解决的问题分解为若干个规模较小、相互独立、与原问题形式相同的子问题。

2、治理：求解各个子问题，由于子问题与原问题形式相同，只是规模较小，当子问题划分得足够小时，就可以使用简单的方法解决。

3、合并：按原问题的要求，将子问题的解逐层合并以构成原问题的解。

归并排序

1、问题分析

归并排序是一种稳定的排序方法，它的基本思想是将待排序的元素分解成两个规模大致相等的子序列，如果不易分解，继续将子序列分解，直到子序列中包含的元素个数为1，因为单个元素的序列本身就是有序的，此时便可以合并，从而得到一个完整的有序序列。

2、算法设计

（1）分解：将待排序的元素分成大小大致一样的两个子序列。

（2）治理：对两个子序列进行排序。

（3）合并：将排好序的有序子序列进行合并，得到最终的有序序列。

3、算法分析

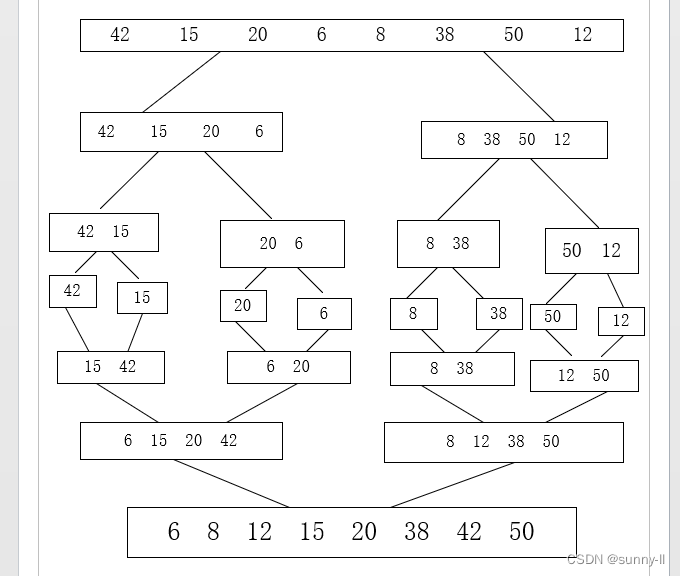
给定一个无序的数列，42，15，20，6，8，38，50，12），进行归并排序，步骤如下：

1、将待排序的元素分成大小大致相同的两个序列。

2、再把子序列分成大小大致相同的两个子序列。

3、如此下去，直到分解成一个元素停止，这时含有一个元素的子序列都是有序的。

4、进行合并操作，将两个有序的子序列合并为一个有序序列，如此下去，直到所有的元素都合并为一个有序序列。

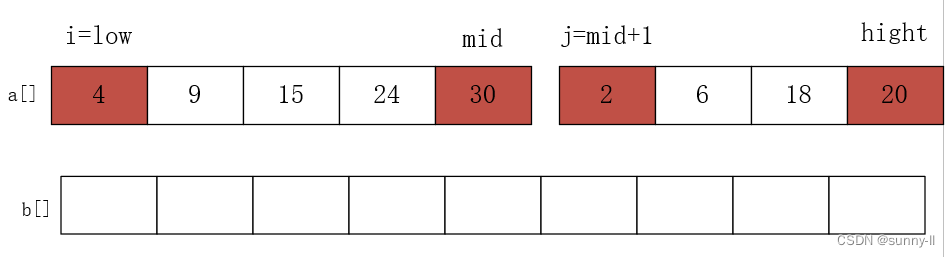
举例而言，下面将以序列（4，9，15，24，30，2，6，18，20）进行图解。

初始化：i = low，j = mid+1，mid = (low+hight)/2，申请一个辅助数组b。

现在比较a[i]和b[j]，将较小的元素放在b数组中，相应的指针向后移动，直到i > mid或者j>hight时结束。

...

较多，建议您继续完善剩余部分，包括具体的图解和代码示例等，这样可以使解释更加清晰易懂。