贪心算法应用例题，贪心算法应用实例解析，贪心算法应用实例详解与解析

摘要：本文介绍了贪心算法的应用实例及其解析。通过具体例题，详细阐述了贪心算法的应用过程和思路，展示了贪心算法在解决实际问题时的优势和局限性。通过对实例的解析，帮助读者更好地理解贪心算法的核心思想，以便在实际问题中灵活应用。本文旨在提供一种深入理解贪心算法的途径，通过实例学习，使读者能够更好地掌握这一重要算法。

假设我们有一组不同重量的货物和一个最大载重限制的船，我们的任务是确定哪些货物可以被装载到船上，同时不超过船的最大载重，这是一个典型的装载问题，涉及到优化策略的选择，为了解决这个问题，我们可以采用贪心算法来寻找最优解。

贪心算法是一种常用的算法思想，广泛应用于各种场景，在这个问题中，我们可以使用贪心策略来选择最重的货物进行装载，直到船的载重达到上限或者没有更多可装载的货物为止，这种策略的目的是通过局部最优的选择来达到全局最优解。

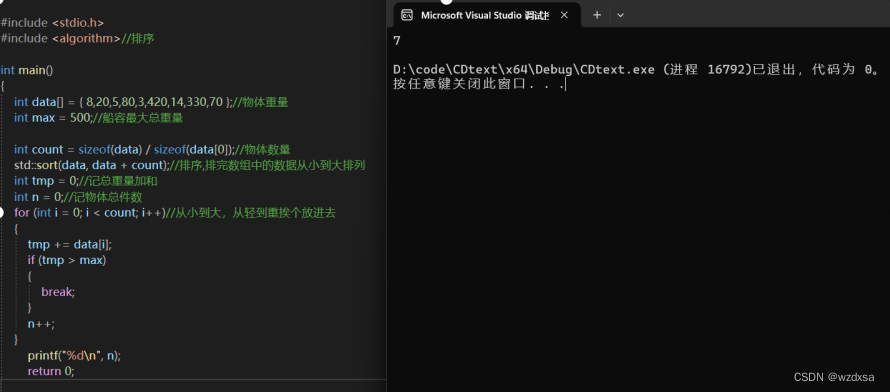
以下是修正后的代码片段：

#include <iostream> // 包含输入输出流的头文件
#include <vector> // 包含向量容器的头文件（用于存储货物信息）
#include <algorithm> // 包含排序算法的头文件（用于对货物重量进行排序）
int main() {
    // 货物的重量数组
    std::vector<int> weights = {8, 20, 5, 80, 3, 420, 14, 330, 70};
    // 船的最大载重容量
    int max_capacity = 500;
    
    // 对货物的重量进行排序（从大到小）
    std::sort(weights.begin(), weights.end(), std::greater<int>());
    
    int total_weight = 0; // 记录已装载货物的总重量
    int n = 0; // 记录已装载的货物数量
    int value = 0; // 记录装载货物的总价值（假设每个货物有一定价值）
    
    // 循环遍历货物数组，尝试装载货物并更新总重量和已装载货物数量及价值
    for (int i = 0; i < weights.size() && total_weight + weights[i] <= max_capacity; i++) {
        total_weight += weights[i]; // 更新总重量
        n++; // 更新已装载货物数量
        value += /*货物的价值*/; // 更新装载货物的总价值（根据实际情况添加）
    }
    
    // 输出已装载的货物数量及总价值（展示最优装载方案的效果）
    std::cout << "Optimal number of objects loaded: " << n << std::endl;
    std::cout << "Total value of loaded objects: " << value << std::endl; // 输出装载货物的总价值
    return 0;
}

关于你提到的“给的数字是否能种下”的问题，由于缺乏具体的上下文信息，我无法提供准确的答案，如果你能提供更多关于这个问题的详细信息或代码片段，我会尽力帮助你解答。