代码随想录day19&day20打卡，代码随想录day19与day20学习心得分享，代码随想录day19与day20学习心得及打卡分享，代码随想录day19与day20，学习心得分享及打卡记录历程回顾标题建议，，代码随想录day19与day20学习心得分享及打卡记录回顾——技术成长之路的点滴印记

摘要：在这篇文章中，作者分享了关于代码随想录day19和day20的学习心得和打卡经历。作者通过学习和实践，掌握了相关的编程知识和技能，并深刻体会到了学习编程的重要性和乐趣。作者也强调了打卡的重要性，通过坚持打卡来记录自己的学习进程和成长。整篇文章旨在分享学习心得和打卡经验，鼓励更多人加入编程学习的行列。

在第19天和第20天的编程学习中，我们深入探讨了编程知识，掌握了新的技能，通过不懈的学习和实践，我们的编程能力得到了显著提高，为未来的项目开发打下了坚实的基础，这次的学习经历更加坚定了我们持续学习的决心，我们期待在未来的日子里能够不断取得更大的进步。

以下是关于二叉树的一些重要概念及解释：

1. 最大深度

我们已经学习了如何判断二叉树的最大深度，最大深度可以通过递归判断左右子节点的深度，然后返回较大的值。

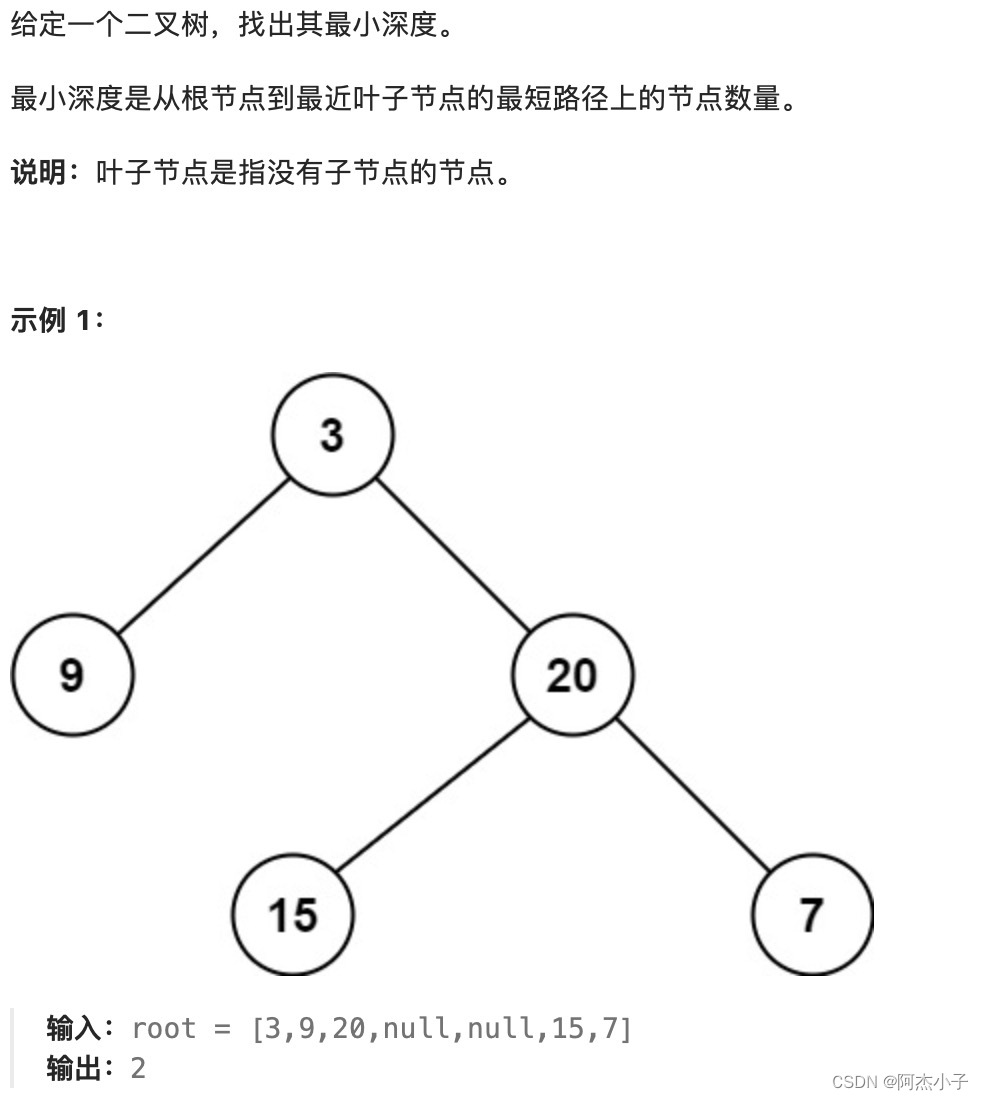
2. 最小深度

最小深度的计算可以通过后序遍历实现，当遇到左子树为空而右子树不为空的情况时，返回右子树的深度加1；当遇到右子树为空而左子树不为空的情况时，返回左子树的深度加1；如果左右子树都不为空，则返回左右子树深度的较小值加1，示例代码如下：

（插入示例代码）

3. 完全二叉树的节点个数

对于完全二叉树，我们可以通过遍历并计数来得知其节点个数，对于任何节点，其左子树的节点数为\(2^{height-level}\)，右子树的节点数为左子树节点数减一（如果存在的话），通过递归遍历每个节点并累加节点数，我们可以得到完全二叉树的节点个数。

4. 平衡二叉树

平衡二叉树是指任何节点的左右子树的高度差的绝对值不超过1的二叉树，我们可以通过递归遍历每个节点并计算其左右子树的高度差来判断一个二叉树是否平衡，如果高度差的绝对值大于1，则该二叉树不是平衡二叉树，示例代码如下：

（插入示例代码）

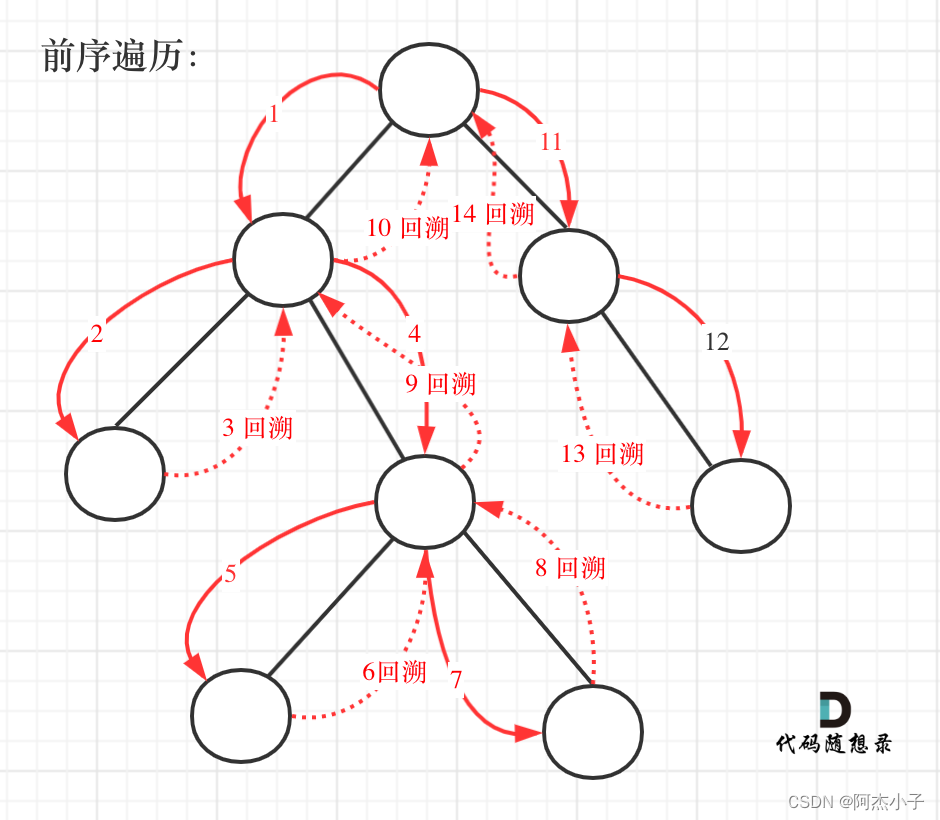
5. 二叉树的所有路径（回溯算法）

我们可以使用回溯算法来寻找二叉树的所有路径，从根节点到叶子节点，在遍历过程中，我们将当前路径加入结果集中，并回溯到上一层路径继续遍历，具体实现较为复杂，建议查阅相关资料或教程以获取更详细的解释和示例代码。

希望以上内容能帮助你更好地理解二叉树的相关概念，通过不断学习和实践，你将更深入地掌握这些概念，并在编程中灵活应用它们。