线性矩阵不等式（LMI）在控制理论中的应用，线性矩阵不等式（LMI）在控制理论中的应用探究，线性矩阵不等式（LMI）在控制理论中的应用及探究

摘要：线性矩阵不等式（LMI）在控制理论中具有重要的应用价值。本文探究了LMI在控制理论中的应用，包括其在系统稳定性分析、优化控制、鲁棒性控制等领域的应用。LMI为控制理论提供了有效的数学工具，有助于解决复杂的控制问题，提高系统的性能。

（一）Matlab中的LMI处理工具包

Matlab中有专门求解线性矩阵不等式的工具包YALMIP，可以在官网上下载安装，可参考yalmip安装教程，yalmip只提供了一些基本的LMI求解方法，有更复杂的不等式求解需求可以再安装cplex工具包，关于怎么使用yalmip工具包可参考yalmip代码编写教程和LMI工具箱教程。

（二）为什么LMI成为控制理论领域重要工具？

线性矩阵不等式（LMI）技术是分析和综合控制系统的重要工具，尤其在鲁棒控制领域中，主要有以下三个原因：

1、对于经典的控制方法，LMI技术的优点就是操作简单，在LMI技术出现以前，人们通过求解Ricaati方程来设计最优控制器，但Ricaati方程求解很难，而LMI技术仅需少量的概念和基本原理就能开发出实用的工具（现在我们可以用YALMIP工具包很方便地求解LMI问题）。

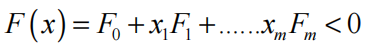
2、LMI技术提供了控制问题的广泛前景，包括鲁棒性分析，标称H∞，H2和鲁棒控制综合，多目标综合，线性参数变化综合等，其中一些无法在古典控制领域中解决处理。

（三）LMI在与Lyapunov不等式的关系

<img alt="" height="36" src="https://img-blog.csdnimg.cn/c802e3b9da49489eaeb88e30c73f15dc.png" width="270">

<img alt="x_1,....x_m" src="https://latex.csdn.net/eq?x_1%2C....x_m">为决策变量，特别地，在上述一般形式中的函数<img alt="" height="20" src="https://img-blog.csdnimg.cn/145708144cbf4139a1edd7fa01bf5c18.png" width="173">为实对称矩阵。<img alt="P" src="https://latex.csdn.net/eq?P">是对称矩阵变量，则应用引理1，可以将上面的矩阵不等式的可行性问题转化成一个等价的矩阵不等式：

<img alt="" height="62" src="https://img-blog.csdnimg.cn/927d3521720b4fba9b2ac56ac64db8e4.png" width="187">

的可行性问题，而后者是一个关于矩阵变量P的线性矩阵不等式。

因此在控制问题中，我们经常要设计Lyapunov函数V(t)，并为了保证系统稳定性要求<img alt="\dot{V}(t)≤0" src="https://latex.csdn.net/eq?%5Cdot%7BV%7D%28t%29%E2%89%A40">，那就可以把<img alt="\dot{V}(t)≤0" src="https://latex.csdn.net/eq?%5Cdot%7BV%7D%28t%29%E2%89%A40">这个不等式转化为线性矩阵不等式的形式，并用matlab中的YALMIP直接求解出即可。

（四）LMI中常见引理

引理2（广义KYP引理[4]）

给定矩阵<img alt="\Theta" src="https://latex.csdn.net/eq?%5CTheta">，<img alt="F" src="https://latex.csdn.net/eq?F">以及<img alt="\Phi" src="https://latex.csdn.net/eq?%5CPhi">，<img alt="\Psi" src="https://latex.csdn.net/eq?%5CPsi">，且<img alt="N_w" src="https://latex.csdn.net/eq?N_w">代表<img alt="T_wF" src="https://latex.csdn.net/eq?T_wF">的零空间，lt;img alt="T_w=\left [ \begin{matrix} I &amp; -jwI \end{matrix} \right ]" src="https://latex.csdn.net/eq?T_w%3D%5Cleft%20%5B%20%5Cbegin%7