图Graph及相关算法（Dijkstra，Kruskal），图Graph及重要算法（Dijkstra与Kruskal详解），图Graph算法详解，Dijkstra与Kruskal算法介绍与解析

摘要：本文介绍了图Graph及其相关算法，包括Dijkstra和Kruskal算法。文章详细解释了这两种算法的原理、实现方法和应用场景。Dijkstra算法主要用于求解单源最短路径问题，而Kruskal算法则用于在图中寻找最小生成树。本文内容对于理解图算法在解决实际问题中的应用具有重要意义。

本文详细探讨了图论中的图及其相关算法，其中包括Dijkstra算法和Kruskal算法，Dijkstra算法用于在加权图中找到从起点到所有其他节点的最短路径，而Kruskal算法则用于解决最小生成树问题，寻找连接所有节点的最小权重边，这些算法在图论和计算机科学领域具有广泛的应用价值。

一、图的概述

1、无向图

2、有向图

3、邻接矩阵

4、邻接表

5、图的广度优先搜索（BFS）和深度优先搜索（DFS）

6、二部图（二分图）

4、简单路径：除起点和终点可能相同外，其他顶点不重复出现的路径。

5、连通性：在含有n个顶点的图中，需要n-1条边才能完全连通，如果图中所有点之间都有路径可通，则称为连通图。

6、子图：子图的顶点集合是原顶点集合的子集，边集合也是原边集合的子集。

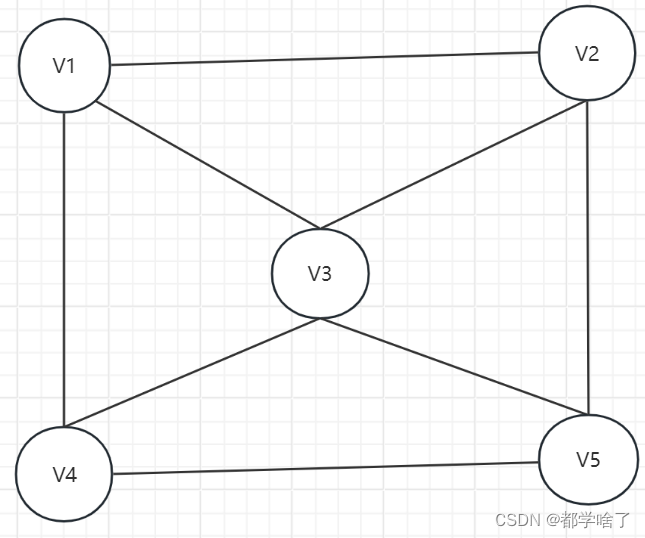
7、极大连通子图（连通分量）：是图中连通性最大的子图。

四、有向图

1、连通图：在有向图中，相异的顶点间存在路径。

2、极大连通子图（强连通分量）：在有向图中，成对顶点间均有路径可通。

五、邻接矩阵与邻接表

邻接矩阵适用于边多的情况，是唯一的；而邻接表适用于边少的情况，不是唯一的，这两种表示方法是描述图结构的主要手段。（此处可添加邻接矩阵和邻接表的图示）

六、图的遍历

图的创建方法包括确定顶点个数，申请并初始化顶点，然后添加边，深度优先搜索（DFS）和广度优先搜索（BFS）是图的两种主要遍历方法。（此处可添加DFS和BFS的伪代码或代码示例）

通过克鲁斯卡尔算法和普里姆算法，我们可以解决最小生成树问题，找到连接所有顶点的最小权重边集。（此处可添加算法示例和结果图示）