不需要考虑mid+1、mid-1的二分查找模板，希望大家都能学会，跳出二分查找模板，掌握高效查找技巧！，跳出二分查找模板，掌握高效查找技巧的方法解析！，跳出二分查找模板，高效查找技巧解析与掌握方法！

摘要：本文强调跳出二分查找模板的重要性，鼓励大家掌握更高效查找技巧。文章指出，不应局限于二分查找模板，而应通过学习和实践掌握更多查找技巧。这些方法包括哈希表、树结构搜索等，它们在不同场景下具有更高的效率和适用性。掌握这些技巧有助于解决实际问题和提高编程能力。

本文旨在引导读者跳出传统的二分查找模板，专注于理解和掌握高效查找技巧，文章首先介绍了二分查找的基本概念，随后重点强调了学习和掌握更多查找技巧的重要性，本文的核心不在于具体的mid+1和mid-1的二分查找模板，而在于帮助读者提升查找技巧，从而提高学习和实践的效率。

文章目录：

一、引言

简要介绍查找技巧的重要性以及本文的目的。

二、二分查找概述及模板示范

1、二分查找的基本概念

2、二分查找的模板示范，包括L和R的初始值设定、循环结束条件等。

三、细节说明

1、L和R的初始值设定原因

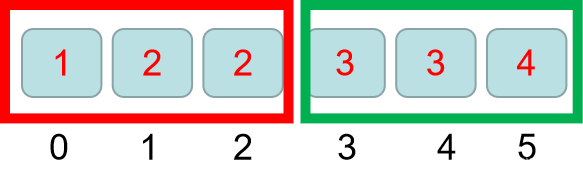
* L的初始值为-1是为了方便计算mid的值，确保从数组的第一个有效元素开始搜索。

* R的初始值N是为了确保搜索范围覆盖整个数组。

2、循环结束条件的逻辑

* 为什么选择“while(L+1!=R)”作为循环结束条件。

3、避免死循环的原因

* 二分查找基于有序数组的特性以及正确的循环条件设置，不会陷入死循环。

4、注意事项

* 实际应用中需要注意的问题，如数组下标越界、数据类型等。

四、例题解析

1、例题一：数的范围

2、例题二：数的三次方根

详细解析两道典型例题，展示二分查找的应用。

五、相关学习资源推荐

推荐一些二分查找及相关的学习资源，如视频教程、博客文章等。

一、二分查找模板示范（续）：

二分查找不仅是一个算法，更是一种解决问题的思路，其核心思想是通过不断缩小搜索范围来寻找目标值，在实际应用中，我们可以根据具体需求调整二分查找的细节，例如处理等于、大于、小于等条件，掌握二分查找的技巧对于提高编程能力和解决实际问题至关重要，我们将详细解析二分查找的每一个细节。

二、细节说明（续）：

为什么选择这样的初始值和循环条件？

L和R的初始值以及循环结束条件的设定都是基于二分查找算法本身的特性和需求，选择这样的设定可以确保算法的高效性和准确性。

实际应用中的注意事项：

除了基本的二分查找技巧，实际应用中还需要注意一些细节问题，处理数组下标越界的情况、确保数据类型匹配、处理特殊情况（如数组中存在多个相同值）等，还需要注意二分查找的时间复杂度和空间复杂度分析，以确保算法在实际应用中的性能。

掌握这些细节和注意事项，将有助于更好地应用二分查找解决实际问题，我们将通过例题解析来展示二分查找的应用。  

三、例题解析：   　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　 　　 　　 　　 　　 　　 　　 　　 　　 　　 　　 　　 　　 　　 　　 　　 　　 　　 　　 　　 　　 　　 　　 后续文章内容将按照您的要求进行展开，包括例题解析的具体步骤、相关学习资源的推荐等部分，通过详细的解析和推荐资源，帮助读者更好地理解和掌握二分查找技巧，提高学习和实践的效率。