MATLAB 之 绘制三维图形的基本函数、三维曲面和其他三维图形，MATLAB三维绘图基础，三维曲面及其他三维图形的绘制函数简介

温馨提示：这篇文章已超过413天没有更新，请注意相关的内容是否还可用！

摘要：，，本文介绍了 MATLAB 中用于绘制三维图形的基本函数和三维曲面等相关内容。通过 MATLAB，可以轻松地创建三维曲面和其他三维图形。基本函数包括绘制三维线图、散点图、柱状图等。还可以利用 MATLAB 绘制各种三维曲面，如平面、立体和曲面图等。这些功能使得 MATLAB 成为数据可视化领域的强大工具。

文章目录

一、绘制三维曲线的基本函数
二、三维曲面
- 1. 平面网格坐标矩阵的生成
- 2. 绘制三维曲面的函数
- 3. 标准三维曲面
- 三、其他三维图形
- - 1. 三维条形图
  - 2. 三维饼图
  - 3. 三维实心图
  - 4. 三维散点图
  - 5. 三维杆图
  - 6. 三维箭头图
    - 三维图形具有更强的数据表现能力，为此 MATLAB 提供了丰富的函数来绘制三维图形。绘制三维图形与绘制二维图形的方法十分类似，很多都是在二维绘图的基础上扩展而来。
      一、绘制三维曲线的基本函数
      - 基本的三维图形函数为 plot3，它是将二维绘图函数 plot 的有关功能扩展到三维空间，用来绘制三维曲线。
      - plot3 函数与 plot 函数用法十分相似，其调用格式如下：
        plot3(x1,y1,z1,选项1,x2,y2,z2,选项2,…,xn,yn,zn,选项n)
        
        其中，每一组 x 、 y 、 z x、y、z x、y、z 组成一组曲线的坐标参数，选项的定义和 plot 函数相同（线型、颜色和标记符号等参数，详见 MATLAB 之二维图形绘制的基本函数和辅助操作）。
        当 x 、 y 、 z x、y、z x、y、z 是同长度的向量时，则 x 、 y 、 z x、y、z x、y、z 对应元素构成一条三维曲线。
        当 x 、 y 、 z x、y、z x、y、z 是同型矩阵时，则以 x 、 y 、 z x、y、z x、y、z 对应列元素绘制三维曲线，曲线条数等于矩阵列数。
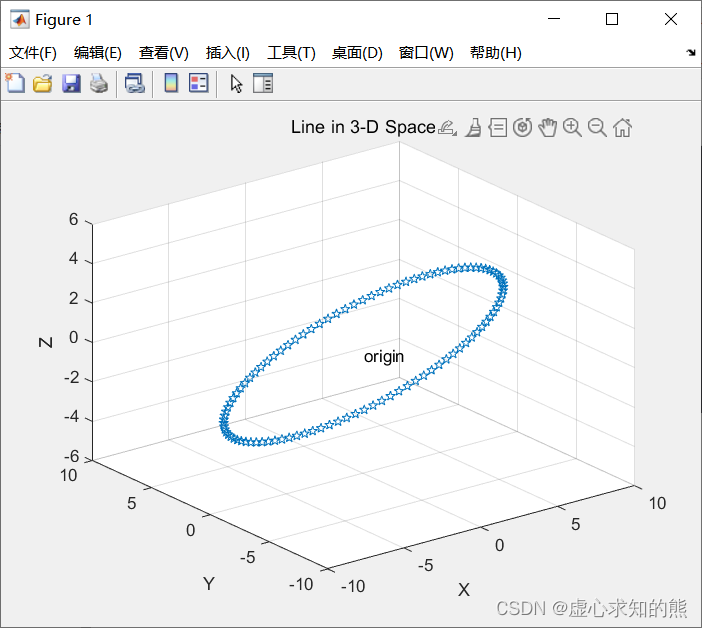
        例如，我们绘制空间曲线： { x 2 + y 2 + z 2 = 64 y + z = 0 \left\{\begin{matrix}x^{2}+y^{2}+z^{2}=64 \y+z=0 \end{matrix}\right. {x2+y2+z2=64y+z=0
        曲线对应的参数方程为 { x = 8 cos ⁡ t y = 4 2 sin ⁡ t z = − 4 2 sin ⁡ t , 0 ≤ t ≤ 2 π \left\{\begin{matrix}x=8\cos t \y=4\sqrt{2} \sin t \z=-4\sqrt{2} \sin t \end{matrix}\right.\begin{matrix},0\le t\le 2\pi \end{matrix} ⎩ ⎨ ⎧x=8costy=42 sintz=−42 sint,0≤t≤2π
        程序如下：
        t=0:pi/50:2*pi; x=8*cos(t); y=4*sqrt(2)*sin(t); z=-4*sqrt(2)*sin(t); plot3(x,y,z,'p'); title('Line in 3-D Space'); text(0,0,0,'origin'); axis ([-10,10,-10,10,-6,6]); xlabel('X'); ylabel('Y'); zlabel('Z'); grid;
        
        程序运行结果如下图所示。
        二、三维曲面
        1. 平面网格坐标矩阵的生成
        绘制 z = f ( x , y ) z=f(x,y) z=f(x,y) 所代表的三维曲面图，先要在 x y xy xy 平面选定一矩阵区域，假定矩形区域 D = [ a , b ] × [ c , d ] D=[a,b]×[c,d] D=[a,b]×[c,d]，然后将 [ a , b ] [a,b] [a,b] 在 x x x 方向分成 m m m 份，将 [ c , d ] [c,d] [c,d] 在 y y y 方向分成 n n n 份。
        由各划分点分别作平行于两坐标轴的直线，将区域 D D D 分成 m × n m×n m×n 个小矩形，生成代表每一个小矩形顶点坐标的平面网格坐标矩阵，最后利用有关函数进行绘图即可。
        产生平面区域内的网格坐标矩阵有以下两种方法。
        （1）利用矩阵运算生成。
        x=a:dx:b; y=(c:dy:d)'; X=ones(size(y))*x; Y=y*ones(size(x));
        
        在上述程序段中，矩阵 X 的 X的 X的每一行都是向量 x x x，行数等于向量 y y y 的元素的个数，矩阵 Y Y Y 的每一列都是向量 y y y，列数等于向量 x x x 的元素的个数。
        于是 X X X 和 Y Y Y相同位置上的元素 ( X ( i , j ) ， Y ( i , j ) (X(i, j)，Y(i, j) (X(i,j)，Y(i,j) 恰好是区域 D D D 的 ( i , j ) (i, j) (i,j) 网格点的坐标。若根据每一个网格点上的 x 、 y x、y x、y坐标求函数值 z z z，则得到函数值矩阵 Z Z Z。
        显然， X 、 Y 、 Z X、Y、Z X、Y、Z 各列或各行所对应坐标，对应于一条空间曲线，空间曲线的集合组成空间曲面。
        （2）利用 meshgrid 函数生成。
        x=a:dx:b; y=c:dy:d; [X,Y]=meshgrid(x,y);
        
        程序段运行后，所得到的网格坐标矩阵 X 、 Y X、Y X、Y与方法（1）得到的相同。当 x = y x=y x=y 时，meshgrid 函数可写成 meshgrid(x)。
        为了说明网格坐标矩阵的用法，下面举一个例子，该例子巧妙地利用网格坐标矩阵来解不定方程。
        例如，已知 6 cylinder(R,30);
        将生成一个正弦型柱面。另外，生成矩阵的大小与 R R R 向量的长度及 n n n 有关。其余用法与 sphere 函数相同。
        MATLAB 还有一个 peaks 函数，称为多峰函数，常用于三维曲面的演示。该函数可以用来生成绘图数据矩阵，矩阵元素由以下函数在矩形区域 [ − 3 , 3 ] × [ − 3 , 3 ] [-3,3]×[-3,3] [−3,3]×[−3,3] 的等分网格点上的函数值确定。 f ( x , y ) = 3 ( 1 − x 2 ) e − x 2 − ( y + 1 ) 2 − 10 ( x 5 − x 3 − y 5 ) e − x 2 − y 2 − 1 3 e − ( x + 1 ) 2 − y 2 f(x,y)=3(1-x^{2})e^{-x^{2}-(y+1)^{2}}-10(\frac{x}{5}-x^{3}-y^{5})e^{-x^{2}-y^{2}}-\frac{1}{3}e^{-(x+1)^{2}-y^{2}} f(x,y)=3(1−x2)e−x2−(y+1)2−10(5x−x3−y5)e−x2−y2−31e−(x+1)2−y2
        例如：
        z=peaks(30);
        
        将生成一个 30 × 30 30×30 30×30 的矩阵 z z z，即分别沿 x x x 和 y y y 方向将区间 [ − 3 , 3 ] [-3,3] [−3,3] 等分成 29 份，并计算这些网格点上的函数值。默认的等分数是 48，即 p=peaks 将生成一个 49 × 49 49×49 49×49 的矩阵 p p p。也可以根据网格坐标矩阵 x 、 y x、y x、y 重新计算函数矩阵。例如：
        >> [x,y]=meshgrid(-5:0.1:5); >> z=peaks(x,y);
        
        生成的数值矩阵可以作为 mesh、surf 等函数的参数而绘制出多峰函数曲面图。另外，若在调用 peaks 函数时不带输出参数，则直接绘制出多峰函数曲面图。
        例如，我们绘制标准三维曲面图形。
        程序如下：
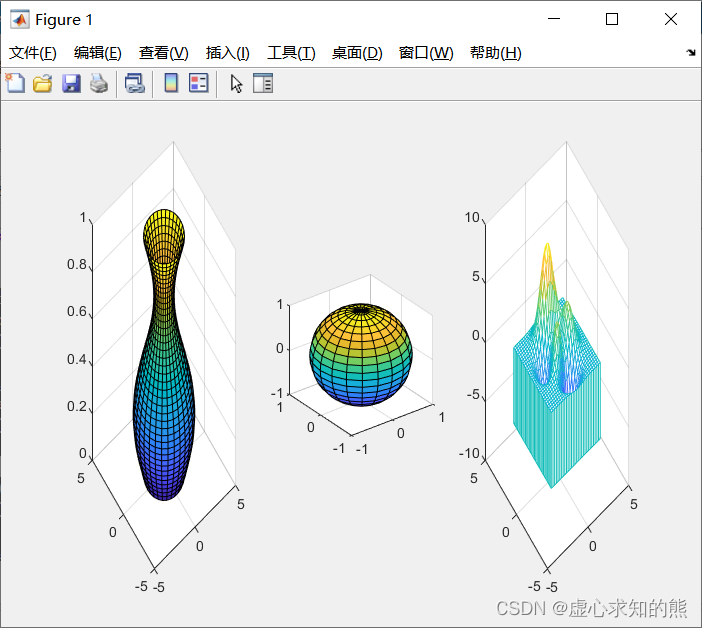
        t=0:pi/20:2*pi; [x,y,z]=cylinder(2+sin(t),30); subplot(1,3,1); surf(x,y,z); %生成一个正弦型柱面 axis([-5,5,-5,5,0,1]); [x,y,z]=sphere; subplot(1,3,2); surf(x,y,z); %生成一个球面 axis equal; [x,y,z]=peaks(30); subplot(1,3,3); meshz(x,y,z); %生成一个多峰曲面 axis([-5,5,-5,5,-10,10]);
        
        程序运行结果如下图所示。
        三、其他三维图形
        在介绍二维图形时，曾提到各种特殊图形，有些还可以以三维形式出现，使用的函数包括 bar3、bar3h、 pie3、 fill3、 scatter3、 stem3 和 quiver3。
        1. 三维条形图
        bar3 函数绘制三维条形图，常用格式如下：
        bar3 (y) bar3(x,y)
        
        在第一种格式中， y y y 的每个元素对应于一个条形。第二种格式在 x x x 指定的位置上绘制 y y y 中元素的条形图。
        bar3h 的用法与 bar3 相同。
        2. 三维饼图
        pie3 函数绘制三维饼图，常用格式如下：
        pie3(x,explode)
        
        其中 x x x 为向量，用 x x x 中的数据绘制一个三维饼图，explode 设置相应的扇形是否偏离整体图形。
        3. 三维实心图
        fill3 函数可在三维饼图内绘制出填充过的多边形，常用格式如下：
        fill3(x,y,z,c)
        
        其中使用 x 、 y 、 z x、y、z x、y、z 作为多边形的顶点，而 c c c 指定了填充的颜色。
        4. 三维散点图
        scatter3 函数可在三维空间内绘制散点图，常用格式如下：
        scatter3(x,y,z,c)
        
        其中 x 、 y 、 z x、y、z x、y、z 必须时等长度的向量，而 c c c 指定了填充的颜色。
        5. 三维杆图
        stem3 函数绘制离散序列数据的三维杆图，常用格式如下：
        stem3(z) stem3(x,y,z)
        
        第一种将数据序列 z z z 表示为从 x y xy xy 平面向上延申的杆图， x x x 和 y y y 自动生成。第二种格式在 x x x 和 y y y 指定的位置上绘制数据序列 z z z 的杆图。
        6. 三维箭头图
        quiver3 函数绘制三维空间的矢量图，常用格式如下：
        quiver3(x,y,z,u,v,w)
        
        其中 x 、 y 、 z 、 u 、 v 、 w x、y、z、u、v、w x、y、z、u、v、w 必须长度一样，绘制三维矢量图。矢量由 ( u , v , w ) (u,v,w) (u,v,w) 决定，所在位置由 ( x , y , z ) (x,y,z) (x,y,z) 决定。例如，quiver3(1,2,3,4,5,6) 是以 (1,2,3) 为起点绘制一个矢量，即一个由 (1,2,3) 指向 (4,5,6) 的箭头。
        例如，我们绘制以下三维图形。
        （1）绘制魔方阵的三维条形图。
        （2）已知 x = [ 2347 , 1827 , 2043 , 3025 ] x=[2347,1827,2043,3025] x=[2347,1827,2043,3025]，绘制三维饼图。
        （3）用随机的顶点坐标值画出 5 个黄色三角形。
        （4）以三位杆图形式绘制曲线 y = sin ⁡ x y=\sin x y=sinx。
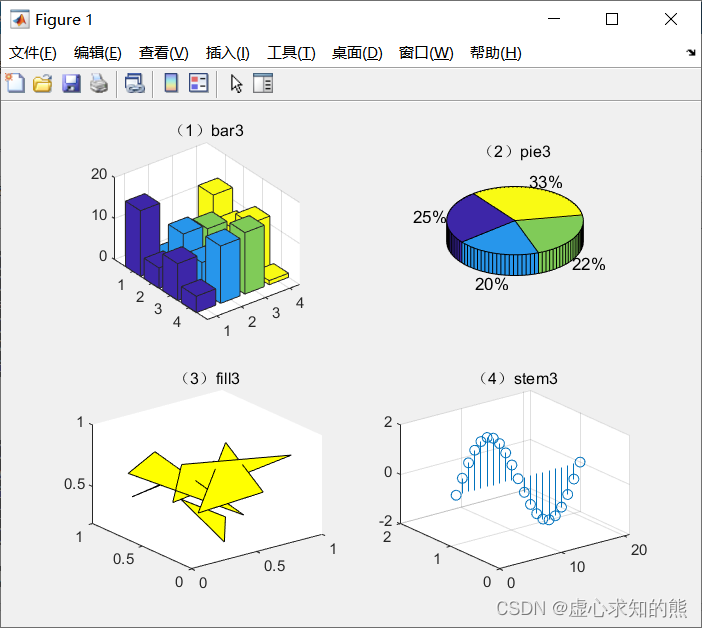
        整体程序如下：
        subplot(2,2,1); bar3(magic(4)); title('（1）bar3'); subplot(2,2,2); pie3([2347,1827,2043,3025]); title('（2）pie3'); a=rand(3,5); b=rand(3,5); c=rand(3,5); subplot(2,2,3); fill3(a,b,c,'y'); title('（3）fill3'); y=2*sin(0:pi/10:2*pi); subplot(2,2,4); stem3(y); title('（4）stem3');
        
        整体程序运行结果如下图所示。
        除了上面讨论的三维图形外，常用图形还有瀑布图、三维曲面的等高线图。
        绘制瀑布图用 watrall 函数，它的用法及图形效果与 meshz 函数相似，只是它的网格线是在 x x x 轴方向出现，具有瀑布效果。等高线图分二维和三维两种形式，分别使用函数 contour 和 contour3 绘制。
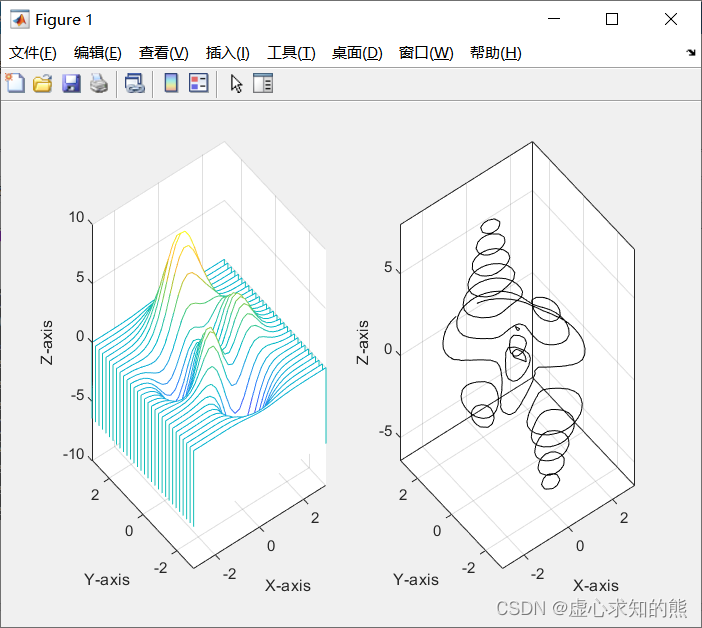
        例如，我们绘制多峰函数的瀑布图和等高线图。
        程序如下：
        subplot(1,2,1); [X,Y,Z]=peaks(30); waterfall(X,Y,Z) xlabel('X-axis'); ylabel('Y-axis'); zlabel('Z-axis'); subplot(1,2,2); contour3(X,Y,Z,12,'k'); %其中12代表高度的等级数 xlabel('X-axis'); ylabel('Y-axis'); zlabel('Z-axis');
        
        程序运行结果如下图所示。