【C++练级之路】【Lv.15】AVL树（双子旋转，领略绝对平衡之美），C++练级之路，AVL树的双子旋转与绝对平衡之美（Lv.15），C++练级之路，AVL树的双子旋转与绝对平衡之美（Lv.15详解）

摘要：本文介绍了C++练级之路中的Lv.15内容，聚焦于AVL树的双子旋转和绝对平衡之美。通过深入解析AVL树的平衡机制，展示了如何通过双子旋转实现树的平衡调整，使读者领略到AVL树在数据结构和算法领域的独特魅力。本文旨在为C++学习者提供AVL树的相关知识，帮助其在数据结构和算法领域进一步提升技能。

关于AVL树的概念

AVL树是一种自平衡二叉搜索树，由两位俄罗斯数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明，它的核心思想是通过对二叉搜索树的调整，使得树的高度保持在最低限度，从而实现高效的搜索、插入和删除操作，AVL树的左右子树都是AVL树，且任意节点的左右子树高度差的绝对值不超过1，这使得AVL树几乎完美接近于平衡，从而保证了其优良的搜索性能。

AVL树的模拟实现

在AVL树的实现中，我们可以使用三叉链结构，增加指向父节点的指针，以便在旋转操作时追踪节点，节点存储键值对和平衡因子，平衡因子用于记录左右子树的高度差，在实现AVL树时，我们需要定义根节点等成员变量。

AVL树的插入操作

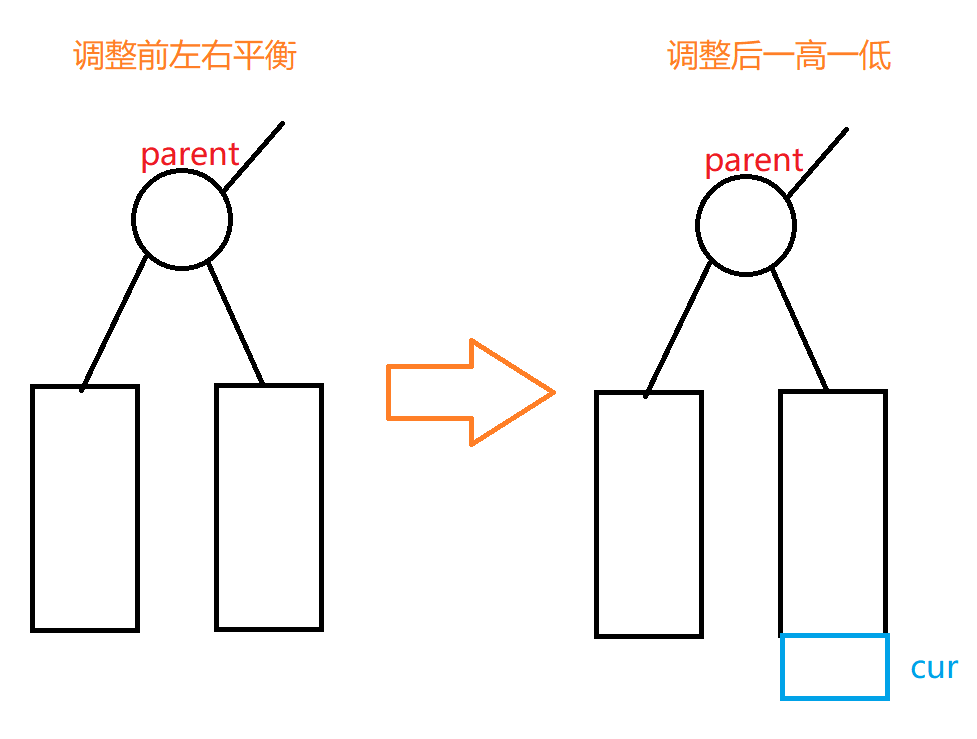
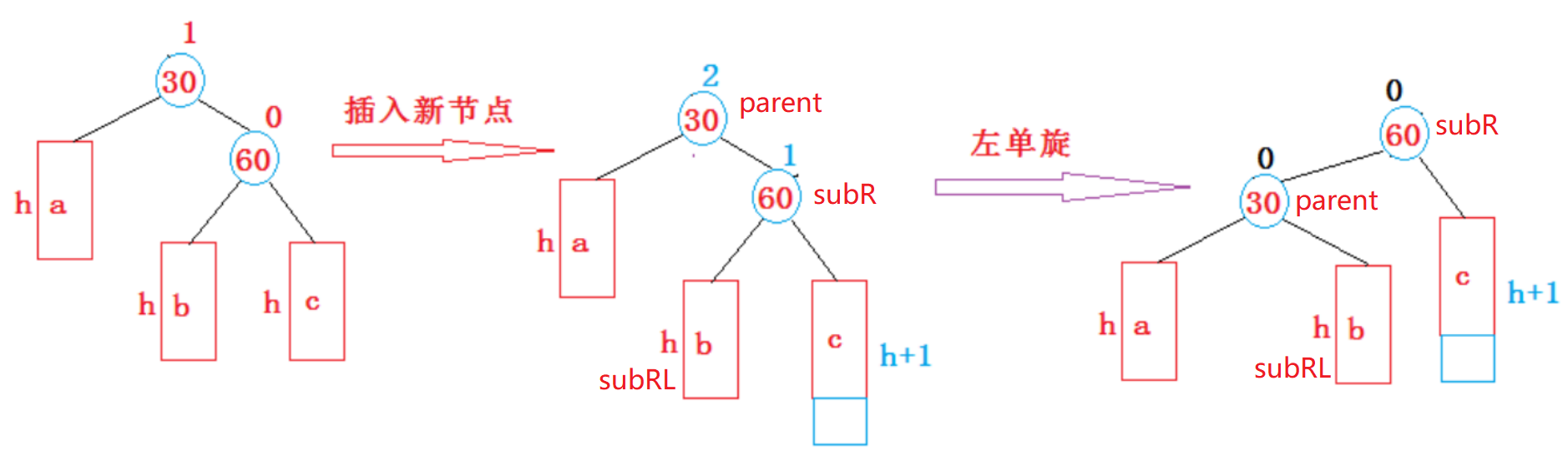
AVL树的插入操作首先遵循二叉搜索树的插入方式，然后关注平衡因子的变化，根据平衡因子的不同值，进行不同的旋转操作来保持树的平衡，旋转操作分为单旋和双旋，单旋包括左单旋和右单旋，双旋包括左右旋和右左旋，每种旋转操作都有其特定的应用场景和目的。

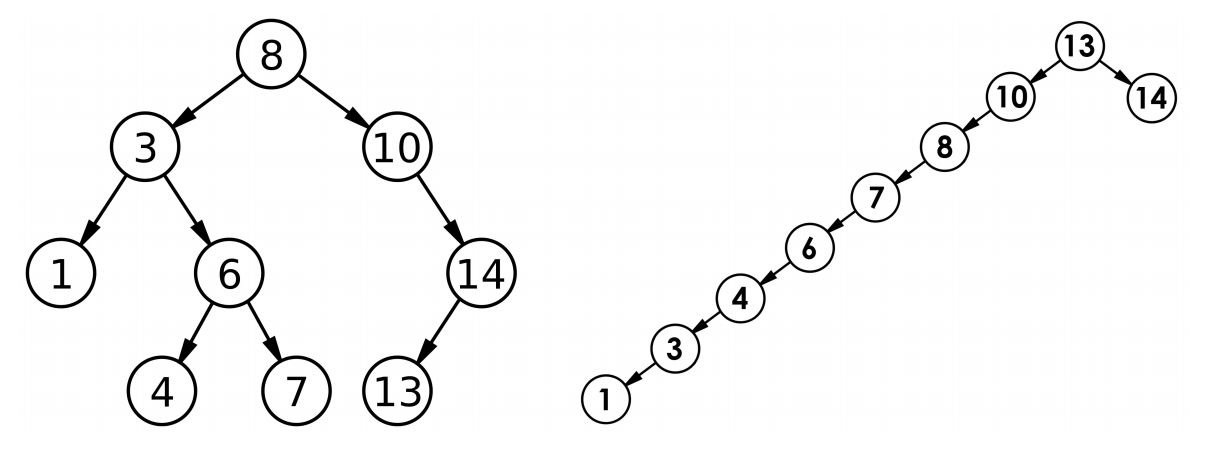
AVL树的验证与性能

验证AVL树的主要方式是检查其左右子树的高度是否平衡，通过递归的方式，我们可以验证整棵树的高度平衡性，AVL树的优势在于其优秀的搜索性能、动态调整特性以及良好的平均性能，旋转操作可能增加时间复杂度，并且在某些情况下可能需要更多的存储空间，尽管如此，AVL树在空间开销和性能之间取得了很好的平衡。

适用场景方面，AVL树适用于需要高效搜索、插入和删除操作的数据场景，特别是在数据动态变化的情况下，AVL树能够保持其平衡性，从而提供稳定的性能表现。

在个人主页部分，你可以进一步介绍自己的专栏，分享更多关于C语言、数据结构世界和进击的C++的主题，以及你的写作目的和心得，这将有助于吸引更多读者关注你的专栏，并与之互动。