【LeetCode】LeetCode 547. 省份数量（Java版 什么是并查集），Java实现LeetCode 547. 省份数量详解，并查集概念及应用

摘要：在LeetCode的第547题中，要求统计一个由省份组成的国家中的省份数量。这个问题可以通过使用并查集来解决。并查集是一种数据结构，用于处理一些不交集（Disjoint Sets）的合并及查询问题。在Java中，通过并查集可以有效地处理这种问题，通过合并和查找操作来确定省份的数量。

哈_

期待您的关注😊

题目描述

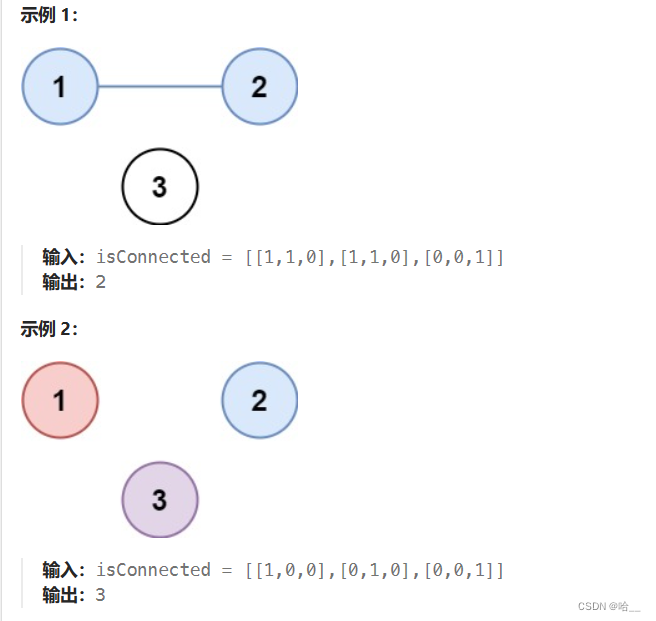
给定一个包含n个城市的连通性矩阵isConnected，其中isConnected[i][j] = 1表示第i个城市和第j个城市直接相连，而isConnected[i][j] = 0表示二者不直接相连，省份是一组直接或间接相连的城市，组内不含其他没有相连的城市，求矩阵中省份的数量。

思路讲解

这是一道关于图的算法的题目，我们需要理解题目的核心要求：将每个城市划分到其所属的省份中，为了实现这一目标，我们可以使用一种称为“并查集”的数据结构。

并查集是一种用于处理图的连通性问题的数据结构，它主要用于将图中的节点进行分类，同一类的节点属于同一个集合，在这个问题中，我们可以将每个城市看作是一个节点，如果两个城市直接相连，那么它们应该属于同一个集合（即同一个省份），我们的目标是找到所有独立的集合数量，这就是省份的数量。

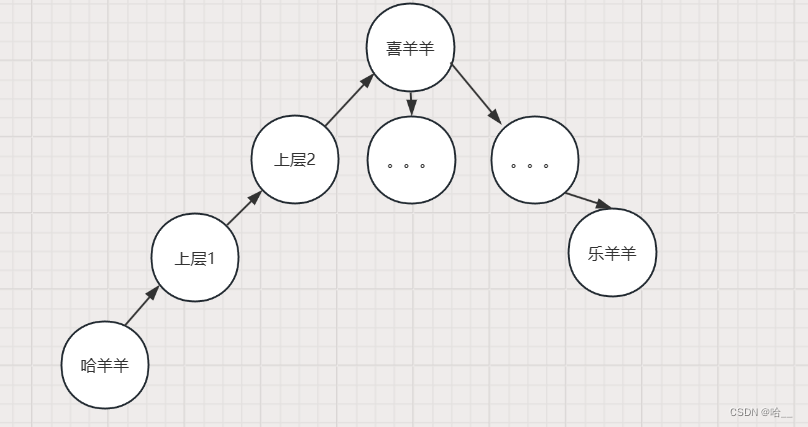
为了更好地理解并查集，我们可以以一个简单的例子来说明：假设有两群羊，一群是喜羊羊，另一群是沸羊羊，每只羊都有一个上层领导者（例如喜羊羊群的首领是喜羊羊），如果我们想知道某只羊属于哪个群体，只需找到它的上层领导者即可，这就是“查”的过程，如果我们想合并两个群体（例如喜羊羊和沸羊羊合并为一个群体），我们只需将其中一个群体的首领设置为另一个群体的首领即可，这就是“并”的过程，在这个问题中，我们将使用类似的逻辑来合并城市，直到所有城市都被分配到其所属的省份中。

接下来是具体的算法实现：

我们需要一个数组p来记录每个城市（节点）的上层领导者是谁，初始化时，每个城市都是独立的省份，所以每个城市都是自己的领导者（即上层领导者是自己），我们遍历连通性矩阵中的每一对直接相连的城市，并使用并查集将它们合并到同一个省份中，我们统计有多少个独立的领导者（即省份数量），这就是我们的答案。

下面是具体的代码实现（以Python为例）：

class Solution:
    def __init__(self):
        self.p = [i for i in range(n)]  # 初始化每个城市的上层领导者为自己
    
    def find(self, x):  # 查找节点x的领导者（省份代表）
        while x != self.p[x]:  # 如果节点的领导者不是它自己，继续查找它的领导者
            x = self.p[x]  # 沿着路径向上查找直到找到领导者（省份代表）
        return x  # 返回领导者的索引（即省份代表）
    
    def join(self, x, y):  # 将节点x和节点y合并到同一个省份中
        px = self.find(x)  # 找到节点x的省份代表
        py = self.find(y)  # 找到节点y的省份代表
        if px != py:  # 如果它们的省份代表不同（即它们不在同一个省份中）
            self.p[px] = py  # 将一个省份的代表设置为另一个省份的代表，完成合并操作
            return True  # 返回合并成功的信息（这里可以根据实际需求返回其他信息）
        return False  # 返回合并失败的信息（因为它们已经在同一个省份中）
    
    def findCircleNum(self, isConnected):  # 主函数入口点，计算省份数量
        for i in range(n):  # 遍历每个城市节点（节点索引从0开始）
            for j in range(i + 1, n):  # 对于每个城市节点，检查与其直接相连的城市节点（避免重复计算）
                if isConnected[i][j] == 1:  # 如果两个城市直接相连（即它们之间存在一条路径）则将它们合并到同一个省份中
                    self.join(i, j)  # 执行合并操作（使用并查集实现）
        count = 0  # 统计省份数量（独立领导者数量）的计数器初始化为0
        for i in range(n):  # 再次遍历每个城市节点以统计最终的省份数量（独立领导者数量）
            if self.find(i) == i:  # 如果节点的领导者是它自己（即它是一个独立的领导者或省份代表）则增加计数器值并继续下一个循环迭代直到遍历完所有节点为止最终返回计数器的值作为结果返回给调用者函数以完成整个算法的执行过程返回最终的省份数量作为结果输出给调用者函数以完成整个算法的执行过程返回最终的省份数量作为结果输出完成整个算法的执行过程返回最终的省份数量作为结果输出给调用者函数以完成整个