空间统计学，快速理解反距离加权法（IDW），空间统计学中的反距离加权法（IDW），原理与应用解析

摘要：空间统计学中的反距离加权法（IDW）是一种基于距离进行权重分配的插值方法。它通过计算样本点与待预测点之间的距离，并根据距离的倒数来分配权重，从而实现空间数据的快速预测和分析。IDW简单易行，适用于处理具有空间相关性的数据，特别是在样本点分布不均或数据缺失的情况下表现出较高的应用价值。

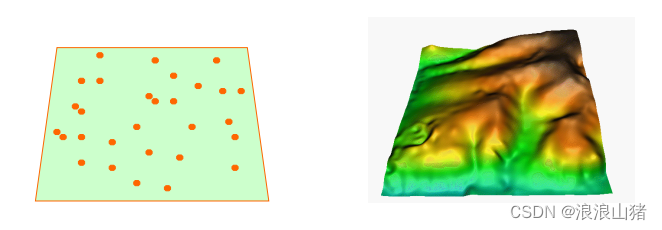
空间插值是一种通过已知数据点来估算未知区域数据值的方法，对于一个平面，我们并不能获取所有区域的精确信息，因此通常通过采样的方式获取部分点的信息，然后通过空间插值计算整个区域的数据。

以反距离加权法（IDW）为例，它是一种常见的空间插值方法，常用于将已知分散的样点数据插值为连续的地表或地下场景，下面是反距离加权法的简要步骤：

1、确定待插值位置和已知样点位置。

2、根据待插值位置与已知样点的距离，计算每个样点的权重，权重与距离的倒数成正比，即距离越近，样点对插值结果的影响越大。

3、使用每个样点的权重对其函数值进行加权平均，得到插值结果。

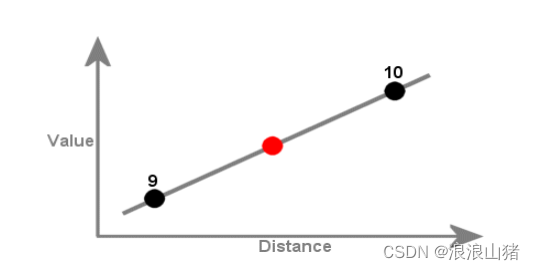
具体地，对于空间上的点来说，未知值的点与样本点之间的距离决定了其最终值的估计，反距离加权法通过结合距离数据和本身的值来计算机位置数据，除了反距离加权法，还有克里金（Kriging）等其他插值方法。

反距离加权法（IDW）的优点是简单易用，在样点分布相对均匀的情况下效果较好，但该方法也存在一些缺点，如插值结果可能呈现出锯齿状特征、函数值抖动等问题，为解决这些问题，可以考虑采用其他空间插值方法，如径向基函数插值（RBF）。

下面是用Python的Matplotlib库生成反距离加权法（IDW）插值示意图的代码：

import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import Rbf  # 引入径向基函数插值库
构造样点数据
np.random.seed(0)  # 设置随机数种子，以便获得可重复的结果
x = np.random.rand(20) * 10 - 5  # 生成20个随机x坐标
y = np.random.rand(20) * 10 - 5  # 生成20个随机y坐标
z = np.sin(np.sqrt(x2 + y2))  # 计算每个样点的函数值
xi, yi = np.meshgrid(np.linspace(-5, 5, 50), np.linspace(-5, 5, 50))  # 生成待插值的网格点坐标
计算插值结果
rbf = Rbf(x, y, z, function='inverse')  # 使用径向基函数插值进行IDW插值计算
zi = rbf(xi, yi)  # 计算网格点的插值结果
绘制示意图
plt.imshow(zi, cmap='rainbow', extent=(-5, 5, -5, 5))  # 绘制插值结果图
plt.colorbar()  # 显示颜色条
plt.scatter(x, y, c=z, cmap='rainbow', edgecolors='black', linewidths=1)  # 绘制样点图
plt.title('Inverse Distance Weighting Interpolation')  # 设置图表标题
plt.xlabel('X')  # 设置X轴标签
plt.ylabel('Y')  # 设置Y轴标签
plt.show()  # 显示图表

在这段代码中：

第一部分通过numpy库生成了随机的二维坐标点和对应的函数值，这些点被视为已知样点，同时生成了待插值的网格点坐标。

第二部分使用scipy库中的Rbf函数进行反距离加权法插值计算，这里的“inverse”参数指定了使用反距离加权法进行计算。

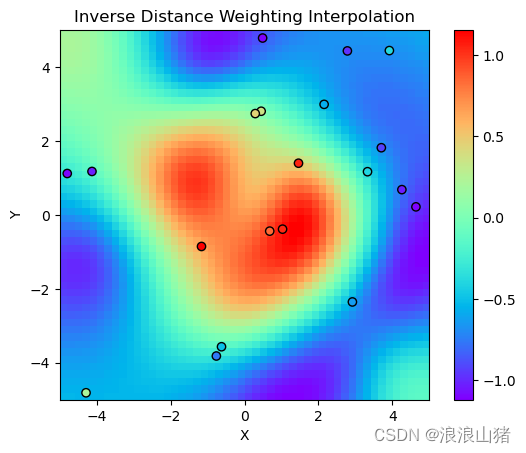
第三部分将插值结果可视化，通过彩虹色来表现不同数值的大小，并添加了散点图来展示已知样点的位置和其对应的函数值，最终生成的图表展示了反距离加权法的插值结果，通过该图可以观察到插值结果的形状和变化趋势，以及样点对插值结果的影响。