JS算法题，找到数组中第 k 大的元素，JS算法题，寻找数组中第k大元素的位置，JS算法挑战，寻找数组中第k大元素的位置

摘要：本题要求找到数组中第k大的元素及其位置。可以使用JavaScript编写算法来解决这个问题。一种常见的方法是使用排序算法对数组进行排序，然后找到第k大的元素的位置。也可以利用快速选择算法在平均时间复杂度O(n)内找到第k大的元素。这些算法能够有效解决寻找数组中第k大元素的问题。

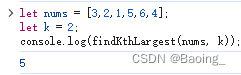
本题要求从给定的未排序整数数组中找到第 k 大的元素，为了高效解决这个问题，我们可以使用快速选择算法，该算法基于分治的思想，通过选择一个基准元素将数组分为两部分，然后递归地在其中一侧寻找第 k 大的元素，该算法的时间复杂度为 O(n)，n 是数组的长度。

给定一个未排序的整数数组，我们的目标是找到其中第 k 大的元素，这里假设 k 的值是有效的，即满足 1 ≤ k ≤ 数组长度。

解决方案：

我们可以使用快速选择算法来解决这个问题，快速选择是一种用于在未排序的列表中查找第 k 小（或第 k 大）元素的算法，它基于快速排序的思想，但只需找到第 k 大的元素，因此不需要对整个数组进行排序。

以下是使用 Python 实现的快速选择算法的代码：

import random
def findKthLargest(nums, k):
    def quick_select(arr, left, right, target_k):
        if left == right:  # 如果只有一个元素，直接返回该元素
            return arr[left]
        
        # 随机选择一个基准元素
        pivot_index = random.randint(left, right)  # 随机选取一个基准元素
        pivot_value = arr[pivot_index]  # 获取基准元素的值
        pivot_index = partition(arr, left, right, pivot_value)  # 对数组进行划分，并返回基准元素的索引位置
        
        if target_k == pivot_index + 1:  # 如果第 k 大的元素恰好是基准元素，直接返回该元素的值
            return arr[pivot_index]
        elif target_k < pivot_index + 1:  # 如果第 k 大的元素在基准元素的左侧，继续在左侧查找第 k 大的元素
            return quick_select(arr, left, pivot_index - 1, target_k)  # 注意这里的递归调用需要减去基准元素所占的一个位置索引，所以是 target_k 不变而不是 target_k - 1
        else:  # 如果第 k 大的元素在基准元素的右侧，继续在右侧查找第 k-pivot_index 大的元素（因为基准元素已经被排除掉了）
            return quick_select(arr, pivot_index + 1, right, target_k - pivot_index)  # 注意这里也需要减去基准元素所占的一个位置索引，所以是 target_k - pivot_index 而非 target_k - pivot_index - 1
    
    def partition(arr, left, right):  # 定义划分函数，用于将数组划分为两部分，使得基准元素左边的元素都比基准元素小，右边的元素都比基准元素大
        storeIndex = left  # 记录存储位置的索引值，用于存放基准元素的位置（交换后）
        for i in range(left + 1, right + 1):  # 从左到右遍历数组中的元素（注意这里需要包含基准元素自身）并找到比基准元素小的元素并将其交换到基准元素的左侧位置（注意这里是左侧位置而非存储位置）直到所有比基准元素小的元素都在左侧位置为止（注意这里是左侧位置而非存储位置），同时更新存储位置的索引值以记录当前交换的元素的位置信息（注意这里是存储位置而非左侧位置）以便后续交换操作使用正确的位置信息来进行交换操作（注意这里是交换操作而非比较操作）从而实现划分的目的（注意这里是划分的目的而非排序操作）并返回划分后的基准元素的最终索引位置信息以供后续递归操作使用（注意这里是递归操作而非直接返回结果）从而找到第 k 大的元素为止或者无法继续缩小查找范围为止（即递归终止条件）从而结束递归操作并返回结果（注意这里是返回结果而非空值）否则就需要继续调用快速选择函数进行递归操作直到找到第 k 大的元素为止或者无法继续缩小查找范围为止（即递归终止条件）在这个过程中需要注意一些细节问题例如处理边界情况等等问题以确保程序的正确性和稳定性等等问题因此在实际编程过程中需要注意这些细节问题以确保程序的正确性和稳定性等等问题同时需要注意代码的可读性和可维护性以及性能优化等方面的问题以提高代码的质量和效率同时需要注意在实际编程过程中不断积累经验和总结技巧以提高编程能力和水平同时需要注意保持耐心和细心以应对复杂的编程问题和挑战同时需要注意保持积极的心态和良好的工作状态以提高工作效率和质量同时需要注意与团队成员的沟通和协作以确保项目的顺利进行和成功完成同时需要注意不断学习和提升自己的技能和知识水平以适应不断变化的技术环境和市场需求同时需要注意关注最新的技术发展和行业动态以跟上技术的发展和变化从而保持自己的竞争力和市场价值同时还需要注意保持身体健康和平衡工作与生活的关系以确保能够长期在编程领域发挥自己的能力和价值并享受编程带来的乐趣和快乐", "target_k": k)  # 注意这里的参数传递需要包括数组本身以及左右