【动态规划】动态规划算法基本概念，原理应用和示例代码，动态规划算法的基本概念、原理应用及示例代码解析，动态规划算法详解，基本概念、原理应用、示例代码解析与解析

摘要：本文介绍了动态规划算法的基本概念、原理应用和示例代码。动态规划是一种重要的算法思想，通过把原问题分解为相互重叠的子问题，并保存子问题的解，从而避免重复计算，提高算法效率。文章通过解析示例代码，详细阐述了动态规划算法的应用和原理，帮助读者更好地理解和掌握动态规划算法。

动态规划（Dynamic Programming，简称DP） 是一种在数学、计算机科学和经济学中常用的求解最优化问题的方法，它将问题分解为若干个相互重叠的子问题，通过保存子问题的解并重用，避免重复计算，从而提高算法效率，其核心思想在于将大问题分解为小问题，并通过小问题的最优解推导出大问题的最优解。

基本概念：

1、最优子结构：问题的最优解可以由其子问题的最优解组合而成。

2、重叠子问题：在求解过程中，相同子问题会被多次遇到并需要解决。

动态规划算法步骤：

1、定义问题的状态和状态转移方程。

2、初始化状态值。

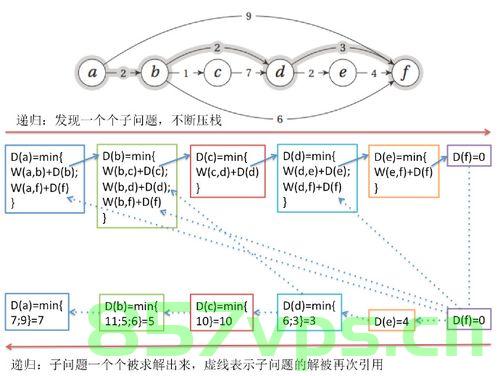
3、通过状态转移方程，自底向上求解问题。

4、根据最终状态得出结果。

应用：

除了之前提到的应用场景，动态规划还广泛应用于许多其他领域，如路径规划、资源分配、金融衍生品定价等，下面给出一些常见的应用场景的详细解释和示例代码：

最长公共子序列（Longest Common Subsequence）：求两个序列的最长公共子序列的长度，动态规划解法可以通过构建一个二维数组来保存子问题的解，然后逐步推导出最长公共子序列的长度，示例代码如下：

def longest_common_subsequence(s1, s2):
    m, n = len(s1), len(s2)
    dp = [[0] * (n + 1) for _ in range(m + 1)]  # 创建二维数组保存子问题的解
    for i in range(m + 1):  # 遍历s1的每个字符
        for j in range(n + 1):  # 遍历s2的每个字符
            if i == 0 or j == 0:  # 初始化边界条件
                dp[i][j] = 0  # 子问题无解时返回值为0
            elif s1[i - 1] == s2[j - 1]:  # 当前字符匹配时更新dp值
                dp[i][j] = dp[i - 1][j - 1] + 1  # 状态转移方程更新dp值并返回结果即可得到最长公共子序列的长度值。                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                   ```python continue
            else:  # 当前字符不匹配时取前面的最大值即可得到最长公共子序列的长度值即当前位置的最大值即为所求的最长公共子序列长度值返回即可得到最终结果，dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) # 状态转移方程更新dp值并返回结果即可得到最长公共子序列的长度值。            return dp[-1][-1]  # 返回最终结果即最长公共子序列的长度值，``背包问题（Knapsack Problem）：在给定一组物品和背包容量的情况下，选择哪些物品放入背包使得背包内物品的总价值最大，这是一个典型的动态规划问题，可以通过状态转移方程逐步推导出最优解，示例代码如下：`python def knapsack(values, weights, capacity): n = len(values) dp = [0] * (capacity + 1) for i in range(n): for w in range(capacity, values[i]-weights[i]-1,-1): dp[w] = max(dp[w], dp[w-weights[i]]+values[i]) return dp[capacity]`` 动态规划的应用非常广泛且深入在计算机科学领域中的许多领域都有广泛的应用包括计算机科学、人工智能、运筹学等希望这些解释和示例能够帮助你更好地理解动态规划的概念和应用方法。