万字长文精解目标检测中的TP、FP、FN、TN、Precision、Recall 、 F1 Score、AP、mAP与AR 。附代码实现。，万字深度解析，目标检测中的关键指标与代码实现详解——TP、FP、FN、TN、Precision、Recall、F1 Score、AP、mAP与AR全解析。

摘要：，，本文详细解析了目标检测中的关键概念，包括TP（真正例）、FP（假正例）、FN（假负例）、TN（真负例）、精确度（Precision）、召回率（Recall）、F1分数（F1 Score）、平均精度（AP）、平均准确率（mAP）和区域召回率（AR）。文章以简洁明了的方式对这些概念进行了全面解读，并附带了代码实现。通过阅读本文，读者可以深入了解目标检测中的评估指标，以便更准确地进行模型性能评估和结果分析。

YOLO目标检测创新改进与实战案例专栏

目录： YOLO有效改进系列及项目实战目录包含卷积，主干注意力，检测头等创新机制以及各种目标检测分割项目实战案例

万字长文精解目标检测中的TP、FP、FN、TN、Precision、Recall 、 F1 Score、AP、mAP与AR 。附代码实现。，万字深度解析，目标检测中的关键指标与代码实现详解——TP、FP、FN、TN、Precision、Recall、F1 Score、AP、mAP与AR全解析。第1张

文章目录

YOLO目标检测创新改进与实战案例专栏
1 .前言
2. “优秀”的目标检测器？

2.1. 两个标准
2.2. 六个指标
2.3 评价步骤
2.4 补充：置信度

总结
2.5 示例
3. COCO评价指标
4. IoU：交并比

4.1 概念
4.2 IoU阈值
**5. 目标检测中的TP、FP、FN、TN**

5.1 二元分类中的TP、FP、FN、TN
5.2 多类分类中的TP、FP、FN、TN
5.3 在目标检测中的TP、FP、FN、TN

5.3.1 **True Positive 真阳性**
5.3.2 **False Positive 假阳性**
5.3.3 **False Negative 假阴性**
5.3.4 **模棱两可的例子**
6. Precision, Recall and F1 Score

6.1 Precision 精确度
6.2 Recall 召回
6.3 F1 Score
6.3 **Precision-Recall** （精确率-召回率，PR）曲线

创建精确率-召回率曲线的具体步骤
代码实现：
更实用的计算PR曲线算法
7. AP — 平均精确度

7.1 COCO11点插值法：COCO 11-Point Interpolation
7.2 代码实现
8. COCO mAP — 平均精度均值

8.1不同IoU阈值下的mAP
8.2 不同物体尺寸的平均精度均值（mAP）

总结
8.3 代码实现
9. 平均召回率（AR）

9.1 如何计算 AR
COCO 评估 API

总结

1 .前言

mAP（Mean Average Precision）是用于评估对象检测和信息检索系统性能的重要指标。它综合考虑了检测结果的精确度（Precision）和召回率（Recall），提供了一个整体的性能评价。

你是否见过下面的表格？这是COCO版本的mAP（即平均精度，他们简称之为AP）。但这个指标到底代表什么呢？这些符号又都代表什么含义呢？在本文中，我们将详细讲解所有必要的理论知识，不仅帮助你解读表格中的数据，还能让你理解采用这种复杂指标的必要性。

Average Precision  (AP) @[ IoU=0.50:0.95 | area=   all | maxDets=100 ] = 0.309
Average Precision  (AP) @[ IoU=0.50      | area=   all | maxDets=100 ] = 0.519
Average Precision  (AP) @[ IoU=0.75      | area=   all | maxDets=100 ] = 0.327
Average Precision  (AP) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = 0.173
Average Precision  (AP) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.462
Average Precision  (AP) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.547
Average Recall     (AR) @[ IoU=0.50:0.95 | area=   all | maxDets=  1 ] = 0.297
Average Recall     (AR) @[ IoU=0.50:0.95 | area=   all | maxDets= 10 ] = 0.456
Average Recall     (AR) @[ IoU=0.50:0.95 | area=   all | maxDets=100 ] = 0.511
Average Recall     (AR) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = 0.376
Average Recall     (AR) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.686
Average Recall     (AR) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.686

2. “优秀”的目标检测器？

2.1. 两个标准

当我们评价一个目标检测器的质量时，主要考虑两个标准：

模型是否预测了物体的正确类别。
预测的边界框是否与真实值非常接近。

2.2. 六个指标

当我们评价一个目标检测器的质量时，通常会使用多种指标来全面评估其性能。以下是常用的评价指标：

Precision（精确度）：
- 精确度表示检测出的对象中，实际为正样本的比例。
- 公式： Precision = True Positives True Positives + False Positives \text{Precision} = \frac{\text{True Positives}}{\text{True Positives} + \text{False Positives}} Precision=True Positives+False PositivesTrue Positives
- Recall（召回率）：
  - 召回率表示所有实际存在的正样本中，被正确检测出来的比例。
  - 公式： Recall = True Positives True Positives + False Negatives \text{Recall} = \frac{\text{True Positives}}{\text{True Positives} + \text{False Negatives}} Recall=True Positives+False NegativesTrue Positives
  - F1-Score：
    - F1分数是精确度和召回率的调和平均值，用来综合衡量模型的性能。
    - 公式： F1-Score = 2 × Precision × Recall Precision + Recall \text{F1-Score} = 2 \times \frac{\text{Precision} \times \text{Recall}}{\text{Precision} + \text{Recall}} F1-Score=2×Precision+RecallPrecision×Recall
    - IoU（Intersection over Union）：
      - IoU 衡量的是预测边界框和真实边界框之间的重叠程度。
      - 公式： IoU = Area of Overlap Area of Union \text{IoU} = \frac{\text{Area of Overlap}}{\text{Area of Union}} IoU=Area of UnionArea of Overlap
      - 通常在计算 True Positives 时会设定一个 IoU 阈值（如 0.5 或 0.75），当预测框与真实框的 IoU 大于等于阈值时，视为正确检测。
      - AP（Average Precision）：
        平均精确度是精确度-召回率曲线下的面积，用来评价单个类别的检测性能。通常在多个不同的 IoU 阈值下计算 AP。
        mAP（Mean Average Precision）：
        平均精确度均值是对所有类别的 AP 取平均值，综合反映整个模型的检测性能。

2.3 评价步骤

在具体的评估过程中，我们通常会按照以下步骤进行：

生成检测结果：
- 对测试数据集进行检测，生成预测边界框及其对应的置信度分数和类别标签。
- 匹配真实框和预测框：
  - 依据 IoU 阈值，将预测框与真实框进行匹配，确定 True Positives、False Positives 和 False Negatives。
  - 绘制精确度-召回率曲线：
    - 计算不同置信度阈值下的精确度和召回率，并绘制精确度-召回率曲线。
    - 计算 AP 和 mAP：
      - 通过插值方法计算每个类别的 AP，再取所有类别的平均值得到 mAP。

通过这些评价指标，我们可以全面了解目标检测器在不同方面的性能，从而指导模型的优化和改进。

2.4 补充：置信度

置信度（Confidence）是机器学习和统计学中的一个概念，用于表示模型对其预测结果的确定程度。在分类问题中，置信度通常表示模型认为某个实例属于某个类别的概率。置信度越高，表示模型对其预测结果越有信心。

例子

假设我们使用一个分类模型来预测图片中的物体类型，模型的输出结果包含每个类别的置信度分数。例如，一张包含水果的图片，模型预测如下：

苹果：置信度 0.8
香蕉：置信度 0.15

橙子：置信度 0.05

在这个例子中，模型认为图片中的物体是苹果的置信度最高（0.8），因此模型预测该物体是苹果。

使用置信度的场景

阈值设置：可以设定一个置信度阈值，仅当置信度超过该阈值时才接受模型的预测。例如，如果置信度低于 0.6，模型可能会输出“不确定”或请求人工验证。
排序和选择：在信息检索或推荐系统中，可以根据置信度对结果进行排序，优先展示置信度高的结果。
模型评估：在评估模型性能时，可以分析不同置信度下的精确率、召回率和 F1 Score，以确定模型在不同置信度水平下的表现。

置信度与置信区间

置信度与置信区间不同。置信区间在统计学中用于估计参数的范围，并附有一个置信水平（例如95%），表示估计的可靠性。而置信度是一个单一的概率值，表示模型对某个具体预测的信心。

总结

置信度在机器学习中是一个重要指标，用于衡量模型对其预测结果的确定程度。理解和正确使用置信度可以帮助提高模型的实际应用效果和决策准确性。

2.5 示例

先看看下面的猫咪检测结果。凭感觉1和2都挺准确的，但是到底哪个更准确呢？这个决策好像很难，这是因为这确实是一个复杂的问题，而且还会变得更加繁琐。我们通常对检测器处理不同尺寸物体的能力感兴趣。有些检测器在识别小型物体时可能表现不佳，但对大型物体的识别则较为出色。而另一些检测器虽然整体表现一般，但在小物体的识别上可能更为精准。那么，一个模型同时检测多个物体的能力如何？正如你所见，这并不是一个简单的问题。COCO评估指标就是为了全面评估这些性能而设计的。

在目标检测任务中，图像中的绿框和红框分别代表以下含义：

Ground Truth（绿框）：
- 定义：绿框表示图像中真实存在的目标的边界框。这些框通常是由人工标注或通过其他准确的标注方法获得的，是对图像中物体位置和类别的准确描述。
- 用途：绿框用于评估检测模型的性能。通过与预测框进行比较，可以判断模型的检测准确性。
- Prediction（红框）：
  - 定义：红框表示目标检测模型预测出的物体边界框。这些框由模型根据输入图像生成，并附带一个置信度分数，表示模型对该预测的信心程度。
  - 用途：红框用于与真实框（绿框）进行比较，从而评估模型的性能指标如平均精确度（AP）和平均召回率（AR）。

万字长文精解目标检测中的TP、FP、FN、TN、Precision、Recall 、 F1 Score、AP、mAP与AR 。附代码实现。，万字深度解析，目标检测中的关键指标与代码实现详解——TP、FP、FN、TN、Precision、Recall、F1 Score、AP、mAP与AR全解析。第2张

3. COCO评价指标

下面这些名词你可以先不用理解，等看完文章后在回过头来看看。

COCO评估指标是用于评估目标检测算法性能的一套标准，广泛应用于计算机视觉领域。COCO（Common Objects in Context）是一个著名的数据集和挑战赛，包含大量不同场景中的物体。COCO评估指标设计精细，能够全面评估目标检测模型的各方面性能。

多样性：
- COCO 数据集包含了多种类、多尺度、多样化的场景和物体，覆盖了自然场景中广泛存在的物体类型和环境，能够更好地反映目标检测器在实际应用中的表现。
- 全面性：
  - COCO 评价指标不仅考虑了平均精确度（AP），还包括了不同 IoU 阈值（如 AP50 和 AP75）下的精确度，以及对不同大小物体（小物体、中等物体、大物体）的检测性能，提供了全面的评估维度。
  - 除了精确度，COCO 还提供了召回率（AR）的评估，使得对模型的检测能力有更全面的了解。
  - 严格性：
    - 主指标 AP@[IoU=0.50:0.95] 要求在多个 IoU 阈值下计算平均精确度，从而避免了仅关注单一阈值可能带来的偏差，更加严格地评估了模型的精度和稳定性。
    - 这种严格的评估方法能够有效防止模型在某些特定条件下表现优异，但在其他条件下表现不佳的情况。
    - 标准化：
      - COCO 数据集和其评价指标已成为目标检测领域的标准，广泛应用于学术研究和工业界。使用 COCO 评价指标可以方便地与其他模型进行对比，促进了公平和标准化的比较。
      - 考虑实际应用需求：
        在实际应用中，目标检测器需要处理不同大小、不同置信度和不同复杂度的物体，COCO 的多维度评价指标能够更好地模拟和衡量这种复杂性。
        例如，小物体（AP_S）、中等物体（AP_M）和大物体（AP_L）的评估，可以帮助开发者发现模型在不同尺寸物体检测上的优缺点，从而进行有针对性的改进。

4. IoU：交并比

4.1 概念

要深入了解mAP（平均精度均值），首先需从IoU（intersection over Union ）开始。

IoU（交并比）是用于衡量两个边界框匹配程度的一个指标，通常用来评估预测边界框相对于真实边界框的准确性。

按照定义，IoU是预测框 P 和真实框 G两个边界框的交集与它们的并集之比：

万字长文精解目标检测中的TP、FP、FN、TN、Precision、Recall 、 F1 Score、AP、mAP与AR 。附代码实现。，万字深度解析，目标检测中的关键指标与代码实现详解——TP、FP、FN、TN、Precision、Recall、F1 Score、AP、mAP与AR全解析。第3张

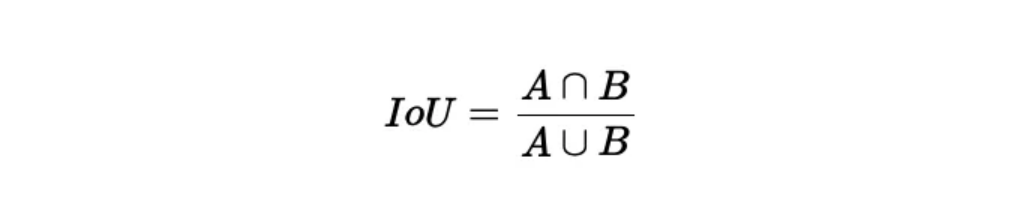
如下图所示，你可以这样理解交集与并集：中间图表示的是并集，右边图标识交集

交集面积（Intersection Area）：P 和 G 重叠的区域。
并集面积（Union Area）：P 和 G 的总面积，去除重叠部分的重复计算。

万字长文精解目标检测中的TP、FP、FN、TN、Precision、Recall 、 F1 Score、AP、mAP与AR 。附代码实现。，万字深度解析，目标检测中的关键指标与代码实现详解——TP、FP、FN、TN、Precision、Recall、F1 Score、AP、mAP与AR全解析。第4张

我们来分析一下这个公式。以下几点值得注意：

并集的大小永远大于或等于交集。
如果两个边界框没有重合部分，交集为零，从而IoU为0。
如果两个边界框完全重合，交集与并集相等，从而IoU为1。
IoU的值总在0到1之间，包括0和1。

IoU的值越大，说明预测框 P 和真实框 G重合越多，说明匹配效果越好！

你可能有时会听到IoU被用一个更专业的名字来称呼：Jaccard指数或Jaccard相似度。

在目标检测领域中，这两者是相同的概念。Jaccard指数是一个更为广泛的数学形式，用于衡量两个有限集合之间的相似性。

在Python中，可以这样计算IoU：

def calculate_iou(box1, box2):
    # box1 and box2 are (x1, y1, x2, y2) format
    x1 = max(box1[0], box2[0])
    y1 = max(box1[1], box2[1])
    x2 = min(box1[2], box2[2])
    y2 = min(box1[3], box2[3])
    
    # Calculate the area of intersection rectangle
    intersection_area = max(0, x2 - x1 + 1) * max(0, y2 - y1 + 1)
    
    # Calculate the area of both the prediction and ground-truth rectangles
    box1_area = (box1[2] - box1[0] + 1) * (box1[3] - box1[1] + 1)
    box2_area = (box2[2] - box2[0] + 1) * (box2[3] - box2[1] + 1)
    
    # Calculate the union area
    union_area = box1_area + box2_area - intersection_area
    
    # Calculate the IoU
    iou = intersection_area / union_area
    
    return iou
# 示例边界框 (x1, y1, x2, y2)
box1 = [50, 50, 150, 150]
box2 = [100, 100, 200, 200]
iou = calculate_iou(box1, box2)
print(f"IoU: {iou}")

现在我们有了一个衡量指标，可以描述一个预测的边界框与实际边界框相比的优劣。在目标检测任务中，选择合适的 IoU 阈值是评估预测边界框是否有效的关键。

4.2 IoU阈值

让我们继续看看下面猫咪检测的例子。很明显，最右边的预测结果偏差较大，而左边的则是可以接受的。我们的大脑是如何这么快地做出这种判断的呢？那中间的预测结果呢？在比较模型性能时，我们不能仅依赖于主观判断。

万字长文精解目标检测中的TP、FP、FN、TN、Precision、Recall 、 F1 Score、AP、mAP与AR 。附代码实现。，万字深度解析，目标检测中的关键指标与代码实现详解——TP、FP、FN、TN、Precision、Recall、F1 Score、AP、mAP与AR全解析。第5张

通常你会看到这个阈值定义为IoU@0.5，这意味着：“只有那些与真实边界框的交并比大于或等于0.5（即50%）的边界框被认为是正确的。”

常见的 IoU 阈值

IoU @ 0.5：
- 常用阈值：在许多目标检测任务中，IoU ≥ 0.5 被视为一个预测边界框与真实边界框的合理重叠。
- 解释：如果预测边界框与真实边界框的 IoU 大于等于 0.5，则认为该预测是有效的；否则认为是无效的或错误的预测。
- IoU@0.75：
  - 高精度阈值：在一些要求较高精度的应用中，IoU ≥ 0.75 更为严格，用于过滤掉低质量的预测结果。
  - 解释：要求预测边界框与真实边界框高度重叠，以保证检测结果的准确性。
  - IoU@0.9 及以上：
    - 非常高精度阈值：在一些特定的高精度应用（如医疗图像分析）中，可能需要 IoU ≥ 0.9
    - IoU@[0.5:0.05:0.95]
      前三种现在应该很清楚了。最后一种虽然看起来有些复杂，其实很好理解。它指的是多个阈值，意味着：“所有从0.5到0.9的IoU阈值，每隔0.05变化一次。” 如果展开这个表达式，
      你会看到它包括了10个不同的IoU阈值：IoU@[0.5:0.05:0.95] = IoU@0.5, IoU@0.55, IoU@0.60, …, IoU@0.85, IoU@0.90, IoU@0.95
      有时候作者可能会简化这种表达，仅写成IoU@[0.5:0.95]。

在评估目标检测器的性能时，如果作者没有明确指定IoU阈值，通常默认采用的是IoU=0.5。你可能会觉得将0.5作为默认阈值似乎太低了。但实际上，这正反映了目标检测问题的复杂性和挑战性！

以下是一个过滤低质量预测结果的示例代码：

def filter_predictions_by_iou(predictions, ground_truths, iou_threshold=0.5):
    """
    过滤掉 IoU 低于指定阈值的预测结果。
    参数:
    - predictions: 预测边界框列表，每个元素为 (x1, y1, x2, y2) 格式。
    - ground_truths: 真实边界框列表，每个元素为 (x1, y1, x2, y2) 格式。
    - iou_threshold: IoU 阈值，低于该值的预测结果将被过滤掉。
    返回:
    - 高质量预测边界框列表。
    """
    def calculate_iou(box1, box2):
        x1 = max(box1[0], box2[0])
        y1 = max(box1[1], box2[1])
        x2 = min(box1[2], box2[2])
        y2 = min(box1[3], box2[3])
        intersection_area = max(0, x2 - x1 + 1) * max(0, y2 - y1 + 1)
        box1_area = (box1[2] - box1[0] + 1) * (box1[3] - box1[1] + 1)
        box2_area = (box2[2] - box2[0] + 1) * (box2[3] - box2[1] + 1)
        union_area = box1_area + box2_area - intersection_area
        iou = intersection_area / union_area
        return iou
    
    high_quality_predictions = []
    for pred in predictions:
        for gt in ground_truths:
            iou = calculate_iou(pred, gt)
            if iou >= iou_threshold:
                high_quality_predictions.append(pred)
                break  # 只要有一个 IoU 满足条件，就保留该预测
    
    return high_quality_predictions
# 示例数据
predictions = [[50, 50, 150, 150], [100, 100, 200, 200], [200, 200, 300, 300]]
ground_truths = [[55, 55, 145, 145], [105, 105, 195, 195]]
# 过滤低于 IoU 阈值 0.5 的预测
filtered_predictions = filter_predictions_by_iou(predictions, ground_truths, iou_threshold=0.5)
print(filtered_predictions)

5. 目标检测中的TP、FP、FN、TN

True Positives,TP：预测为正样本，实际也为正样本的特征数
False Positives,FP：预测为正样本，实际为负样本的特征数
True Negatives,TN：预测为负样本，实际也为负样本的特征数

False Negatives,FN：预测为负样本，实际为正样本的特征数

在机器学习中，分类问题可以根据类别的数量分为二元分类和多类分类：

二元分类（Binary Classification）：
- 这是最简单的分类类型，其中只有两个类别，通常被标记为正类（positive class）和负类（negative class）。
- 任务是预测给定输入数据点属于这两个类别中的哪一个。
- 例如，一个二元分类器可以用来判断电子邮件是否为垃圾邮件，或者一个患者是否患有特定疾病。
- 多类分类（Multi-class Classifiers）：
  - 在多类分类中，有三个或更多的类别，任务是将输入数据点分类到这些类别中的一个。
  - 多类分类器不仅要识别数据点属于正类还是负类，还要确定它属于哪一个具体的类别。
  - 例如，一个多类分类器可以用来识别图像中的物体，如猫、狗、车辆等。

在实际应用中，二元分类可以看作是多类分类的一个特例。在二元分类中，每个数据点的类别是相互排斥的，即要么是A要么是B。在多类分类中，每个数据点同样只能被分类到一个类别，但可选的类别数量大于两个。在一些更复杂的情形中，还有多标签分类（Multi-label Classification），其中一个数据点可以同时属于多个类别。

5.1 二元分类中的TP、FP、FN、TN

我们接下来将探讨的概念包括TP（真阳性）、FP（假阳性）、TN（真阴性）和FN（假阴性），这些术语均来源于二元分类任务。

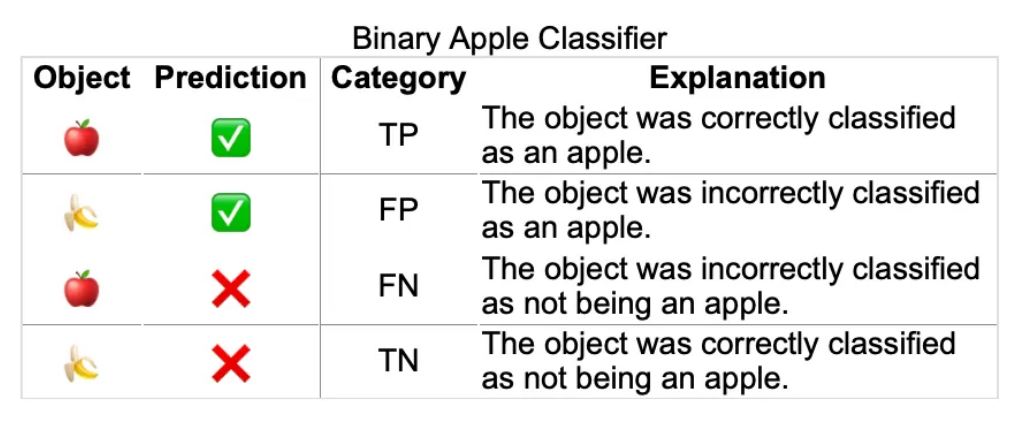
假定我们现在有一个苹果分类器，他是二元分类任务，我们的目标是正确的找到苹果,

定义

True Positive (TP)：把苹果认成了苹果。
False Positive (FP)：把香蕉认成了苹果；
False Negative (FN)：把苹果认成了香蕉。
True Negative (TN)：把香蕉认成了香蕉。也就是没有把香蕉是识别为苹果。

万字长文精解目标检测中的TP、FP、FN、TN、Precision、Recall 、 F1 Score、AP、mAP与AR 。附代码实现。，万字深度解析，目标检测中的关键指标与代码实现详解——TP、FP、FN、TN、Precision、Recall、F1 Score、AP、mAP与AR全解析。第6张

5.2 多类分类中的TP、FP、FN、TN

上述概念在多类分类器中并不完全适用。二元分类器的问题是“此对象是否属于该类别？”，而多类分类器的问题是“此对象属于哪些类别之一？”。幸运的是，我们可以通过采用“一对所有(One-vs-All )”或“一对余(One-vs-Rest )”方法进行推广。这个思路很简单：我们单独评估每个类别，并将其视作一个二元分类器。然后，以下情况成立：

正例：正确预测该对象为讨论中的类别

反例：预测该对象为其他任何类别

在多类模型中，通常不常用TN(真阴性)这一术语，但其可以理解为“那些被正确识别为其他类别的样本”。

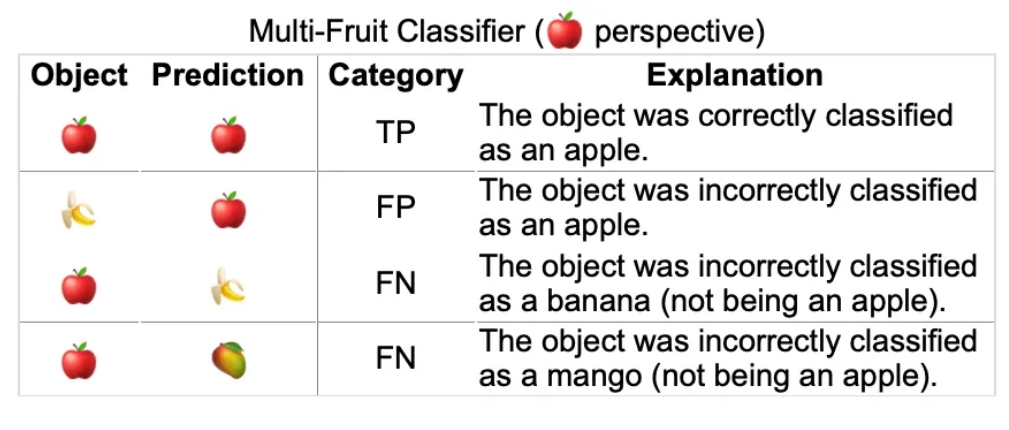
以下是从苹果类的视角出发的示例。也就是我们需要找出苹果是正例。

定义

True Positive (TP)：把苹果认成了苹果。
False Positive (FP)：把香蕉认成了苹果（我们需要找的苹果是正例。但香蕉是不对的。所有叫假阳或假正）；
False Negative (FN)：把苹果认成了香蕉。
True Negative (TN)：把苹果认成了芒果。

万字长文精解目标检测中的TP、FP、FN、TN、Precision、Recall 、 F1 Score、AP、mAP与AR 。附代码实现。，万字深度解析，目标检测中的关键指标与代码实现详解——TP、FP、FN、TN、Precision、Recall、F1 Score、AP、mAP与AR全解析。第7张

现在让我们从香蕉的角度来做一个相似的练习，也就是香蕉是正例。

定义

True Positive (TP)：把香蕉认成了香蕉。
False Negative (FN)：把香蕉认成了苹果。
False Positive (FP)：把苹果认成了香蕉（我们需要找的苹果是正例。但香蕉是不对的。所有叫假阳或假正）；

万字长文精解目标检测中的TP、FP、FN、TN、Precision、Recall 、 F1 Score、AP、mAP与AR 。附代码实现。，万字深度解析，目标检测中的关键指标与代码实现详解——TP、FP、FN、TN、Precision、Recall、F1 Score、AP、mAP与AR全解析。第8张

你是否注意到了什么？

在苹果类的视角中，（🍌, 🍎）组合是一个假阳性FP。但在香蕉类的视角中则是一个假阴性FN。

类似地，（🍎, 🍌）组合在苹果类的视角中是一个假阴性FN，但在香蕉类的视角中是一个假阳性FP。

这里用一种比较无赖的方法去理解：

在苹果类的视角中，苹果是正例。则香蕉是反例。（🍌, 🍎）识别错了，确识别为正例。所以（🍌, 🍎）是假-阳

在香蕉类的视角中，香蕉是正例。则苹果是反例。（🍌, 🍎）识别错了，确识别为反例。所以（🍌, 🍎）是假-阴

5.3 在目标检测中的TP、FP、FN、TN

接下来的问题是：我们该如何将前述概念应用于目标检测器。目标检测器通常属于多类分类器，同时还包括对象定位功能。幸运的是，我们已经拥有了交并比（IoU）这一度量指标！

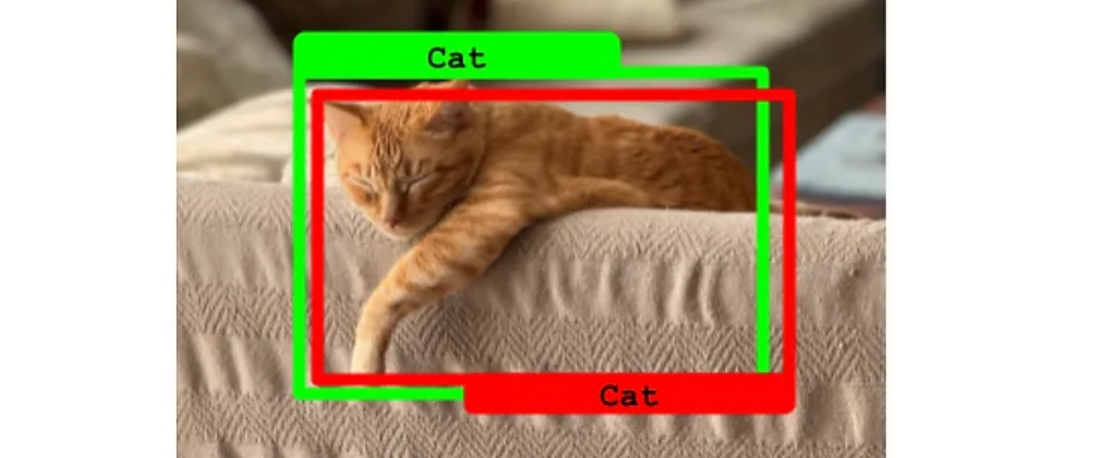
下面我们开始讨论在目标检测中的TP、FP、FN、TN 。并且设定IoU阈值为50%

5.3.1 True Positive 真阳性

当预测的边界框与真实标注的IoU超过50%，并且预测类别与真实类别匹配时，这是一个真阳性的情况。

万字长文精解目标检测中的TP、FP、FN、TN、Precision、Recall 、 F1 Score、AP、mAP与AR 。附代码实现。，万字深度解析，目标检测中的关键指标与代码实现详解——TP、FP、FN、TN、Precision、Recall、F1 Score、AP、mAP与AR全解析。第9张

5.3.2 False Positive 假阳性

预测的边界框与真实标注的IoU低于50%，或者不存在相应的真实标注，或者预测的类别与真实类别不匹配时，这是一个假阳性的情况。

如下图，第一个IoU低于50%，第二个把其他的识别为猫，第三个把猫识别为狮子。

万字长文精解目标检测中的TP、FP、FN、TN、Precision、Recall 、 F1 Score、AP、mAP与AR 。附代码实现。，万字深度解析，目标检测中的关键指标与代码实现详解——TP、FP、FN、TN、Precision、Recall、F1 Score、AP、mAP与AR全解析。第10张

5.3.3 False Negative 假阴性

所有未被预测到的真实标注都是假阴性。如下图，有只猫，没被是被为猫。

万字长文精解目标检测中的TP、FP、FN、TN、Precision、Recall 、 F1 Score、AP、mAP与AR 。附代码实现。，万字深度解析，目标检测中的关键指标与代码实现详解——TP、FP、FN、TN、Precision、Recall、F1 Score、AP、mAP与AR全解析。第11张

5.3.4 模棱两可的例子

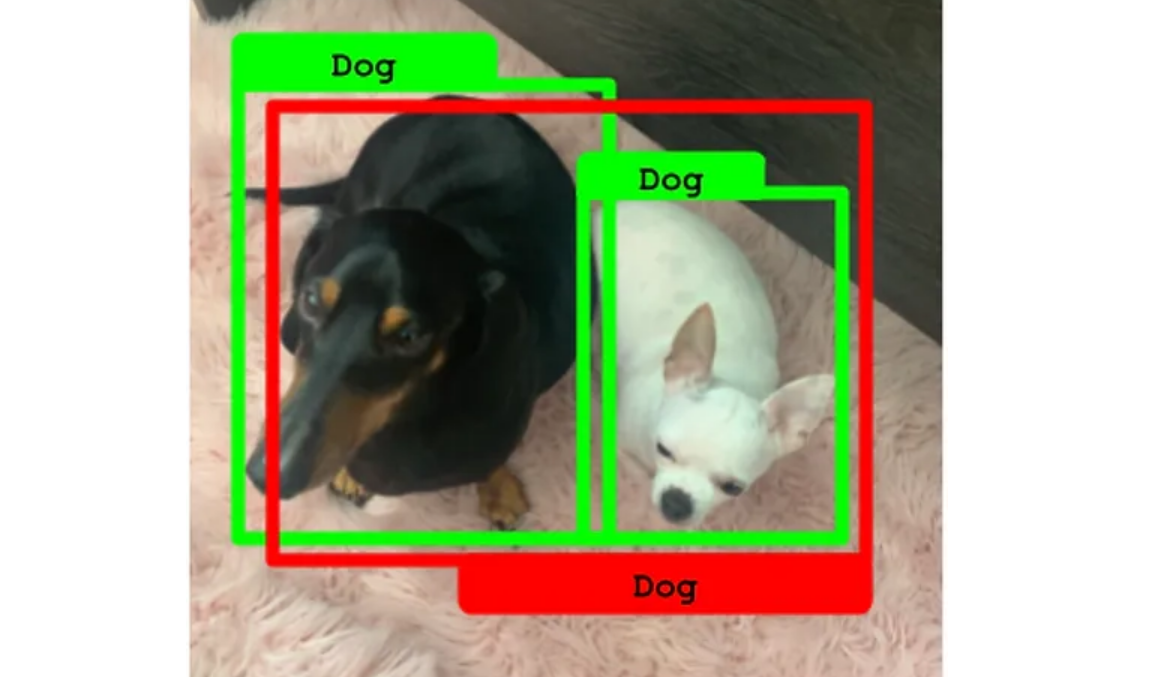
如下图，我们有两个狗子，以及正确的绿色标注。但是但只有一个红色预测框。这种情况下，该预测只能归因于其中一个真实标注（其交并比IoU超过50%）。遗憾的是，另一个真实标注因未被预测到而成为假阴性。这展示了对象检测中对真实标注覆盖不足的处理，强调了提高检测算法的预测覆盖率的重要性。

万字长文精解目标检测中的TP、FP、FN、TN、Precision、Recall 、 F1 Score、AP、mAP与AR 。附代码实现。，万字深度解析，目标检测中的关键指标与代码实现详解——TP、FP、FN、TN、Precision、Recall、F1 Score、AP、mAP与AR全解析。第12张

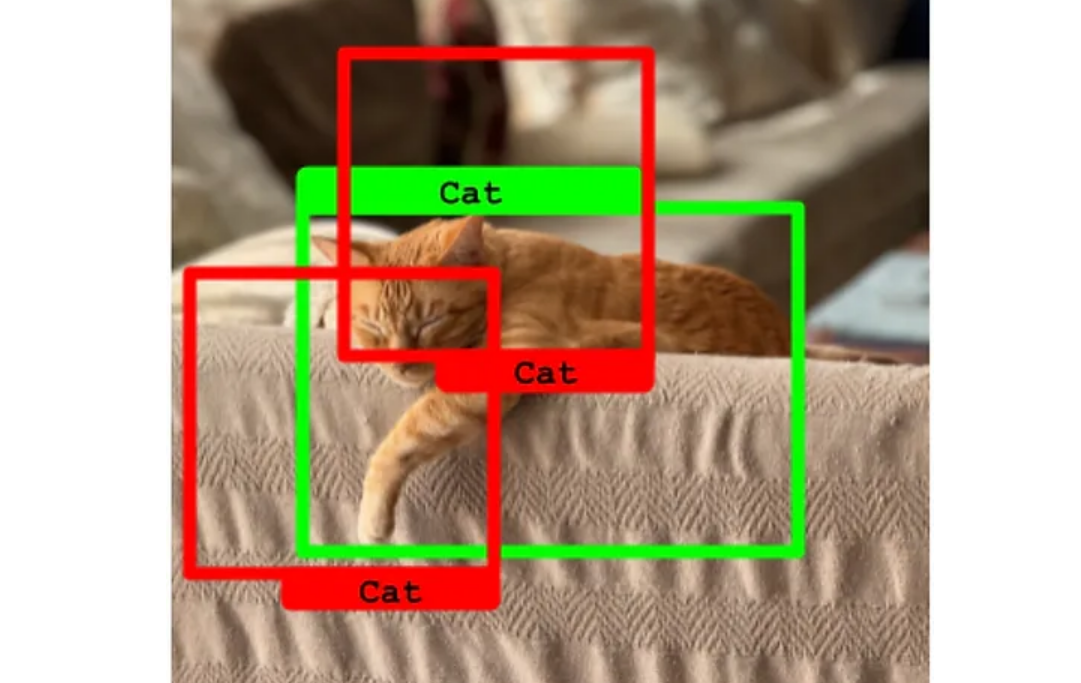
在下面例子中，对同一个真实标注做出了两个预测（红色框），但它们的交并比（IoU）均低于50%。在这种情况下，这两个预测都被视为假阳性，而未能正确预测的真实标注（绿色框）则成为假阴性。这种情况突显了预测的精确度不足，表明了优化预测模型以提高预测质量和准确性的必要性。

万字长文精解目标检测中的TP、FP、FN、TN、Precision、Recall 、 F1 Score、AP、mAP与AR 。附代码实现。，万字深度解析，目标检测中的关键指标与代码实现详解——TP、FP、FN、TN、Precision、Recall、F1 Score、AP、mAP与AR全解析。第13张

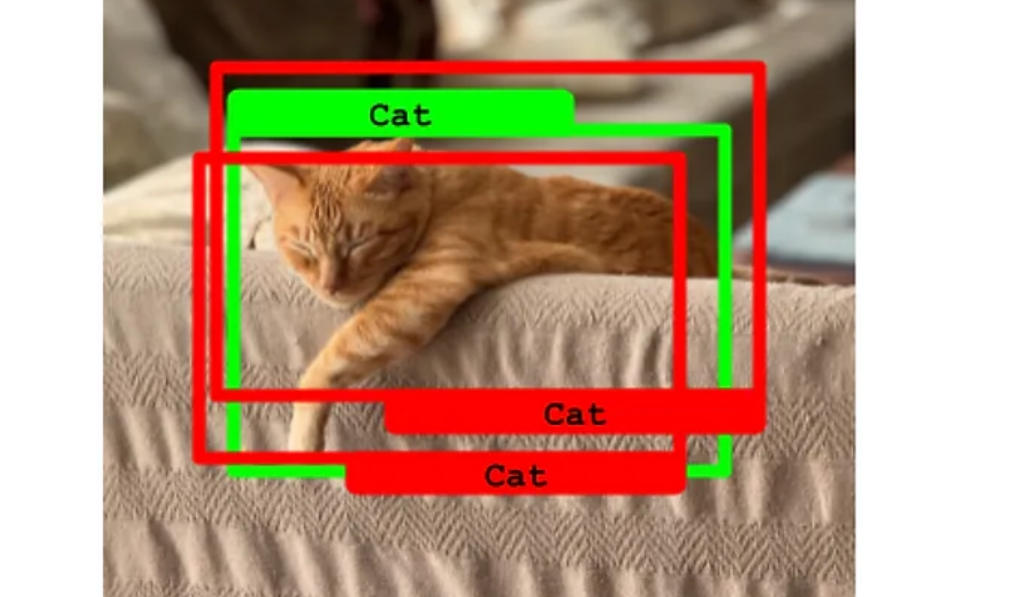
在这最后一个例子中，情况与前述类似，不同之处在于两个预测的交并比（IoU）都高于50%。在这种情况下，交并比最高的那个预测被认为是真阳性，而另一个则被视为假阳性。这种情况说明了在目标检测中，即使多个预测都与真实标注有较高的交并比，我们也需要选择最佳匹配的预测作为真阳性，以优化模型的性能和准确度。

万字长文精解目标检测中的TP、FP、FN、TN、Precision、Recall 、 F1 Score、AP、mAP与AR 。附代码实现。，万字深度解析，目标检测中的关键指标与代码实现详解——TP、FP、FN、TN、Precision、Recall、F1 Score、AP、mAP与AR全解析。第14张

6. Precision, Recall and F1 Score

上面我们已经了解了如何将真正例（TP）、假正例（FP）、真阴性（TN）和假阴性（FN）应用到目标检测器中，我们可以借用其他一些用于分类器的评估指标。这些包括精确率（Precision）、召回率（Recall）和F1分数（F1 Score）。再次强调，这些指标是按类别来衡量的。下面的表格对这些指标进行了总结：

指标	定义	计算公式
精确率	预测为正类中实际为正类的比例	( P r e c i s i o n = T P T P + F P ) ( Precision = \frac{TP}{TP + FP} ) (Precision=TP+FPTP)
召回率	实际为正类中被预测为正类的比例	( R e c a l l = T P T P + F N ) ( Recall = \frac{TP}{TP + FN} ) (Recall=TP+FNTP)
F1分数	精确率和召回率的调和平均数，用于平衡两者之间的关系	( F 1 = 2 ⋅ P r e c i s i o n × R e c a l l P r e c i s i o n + R e c a l l ) ( F1 = 2 \cdot \frac{Precision \times Recall}{Precision + Recall} ) (F1=2⋅Precision+RecallPrecision×Recall)

这些指标帮助我们从不同角度评估目标检测模型的性能，确保模型在准确识别目标的同时，也能尽可能地覆盖所有相关的目标。

6.1 Precision 精确度

精确率（Precision），也称为准确率，是评估分类模型性能的另一个重要指标。精确率表示在所有被模型预测为正类的样本中，实际为正类的比例。其计算公式如下：

精确率 = TP TP + FP \text{精确率} = \frac{\text{TP}}{\text{TP} + \text{FP}} 精确率=TP+FPTP

其中：

TP（True Positive）：模型正确检测到的正样本数量。
FP（False Positive）：模型错误检测到的正样本数量。
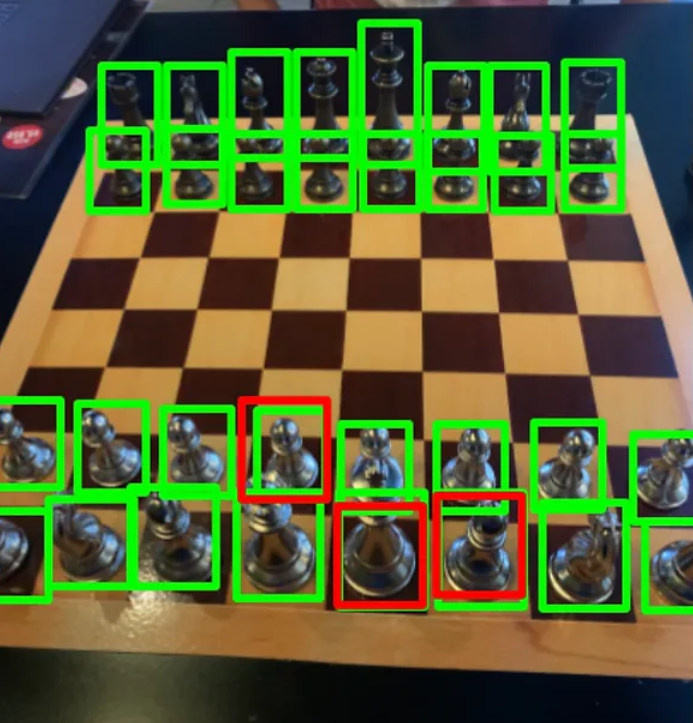
对于一个给定的类别，精确率告诉我们预测为该类别的结果中实际属于该类别的百分比。以下图像显示了一个检测器的结果，其中有3个真正例（True Positives）和1个假正例（False Positive）。因此，精确率的计算如下：
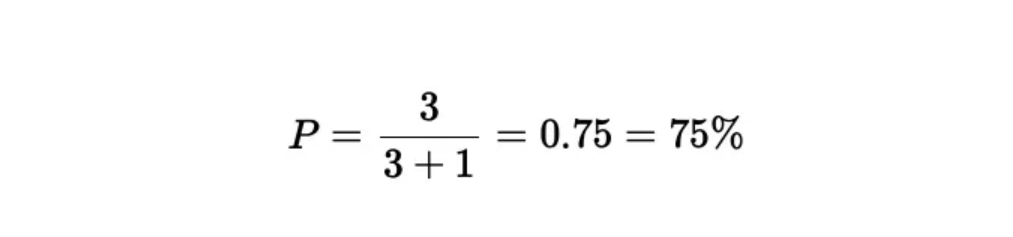
这意味着，精确率为75%，即预测为这个类别的结果中，有75%实际上是正确的。这个指标对于理解模型在特定类别上的预测准确性非常有用。
细心的读者可能已经注意到，精确率的公式并没有考虑假阴性（False Negatives）。仅关注精确率可能会产生误导。
如下示例：正如你所观察到的，尽管精确度指标显示为100%，但模型的整体表现仍不尽人意，主要是由于存在大量的假阴性现象。
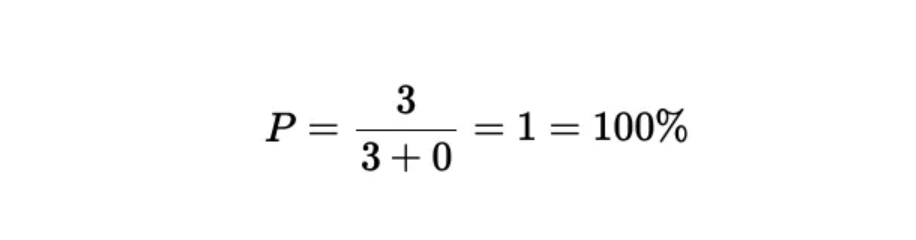
结论：请不要仅通过精确度来评估模型，因为这一指标并未包含假阴性的考量。
6.2 Recall 召回
召回率（Recall），也称为敏感性（Sensitivity），是评估分类模型性能的一个重要指标。召回率表示在所有实际为正类的样本中，被模型正确预测为正类的比例。其计算公式如下：
召回率 = TP TP + FN \text{召回率} = \frac{\text{TP}}{\text{TP} + \text{FN}} 召回率=TP+FNTP
其中：
- TP（True Positive）：模型正确检测到的正样本数量。
- FN（False Negative）：模型未能检测到的正样本数量。
  在下图中像中，正确预测了3个类别实例（真阳性），但还有3个实例未被检测到（假阴性）：
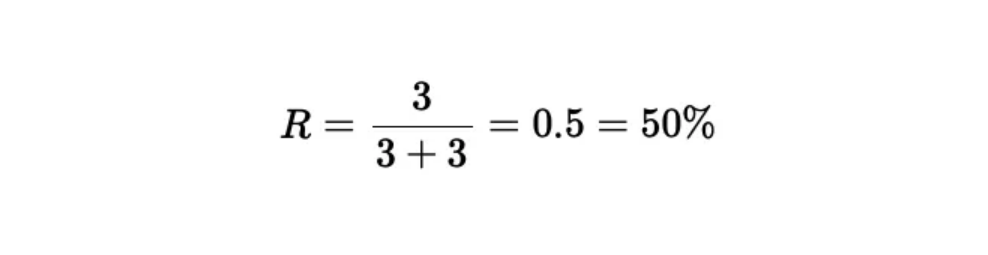
  需要再次强调的是，召回率并未包括假阳性的情况，所以如果单独评估召回率，可能会导致误解。
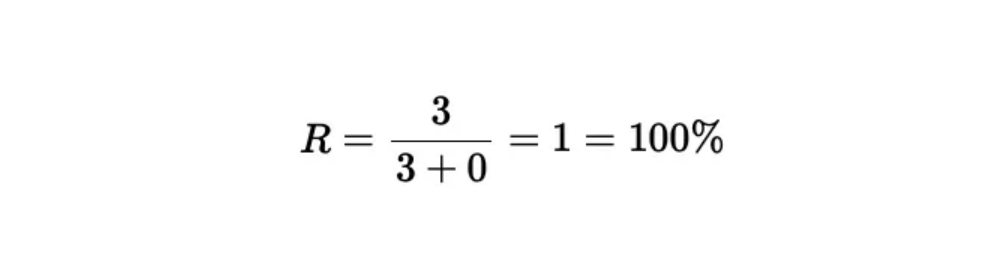
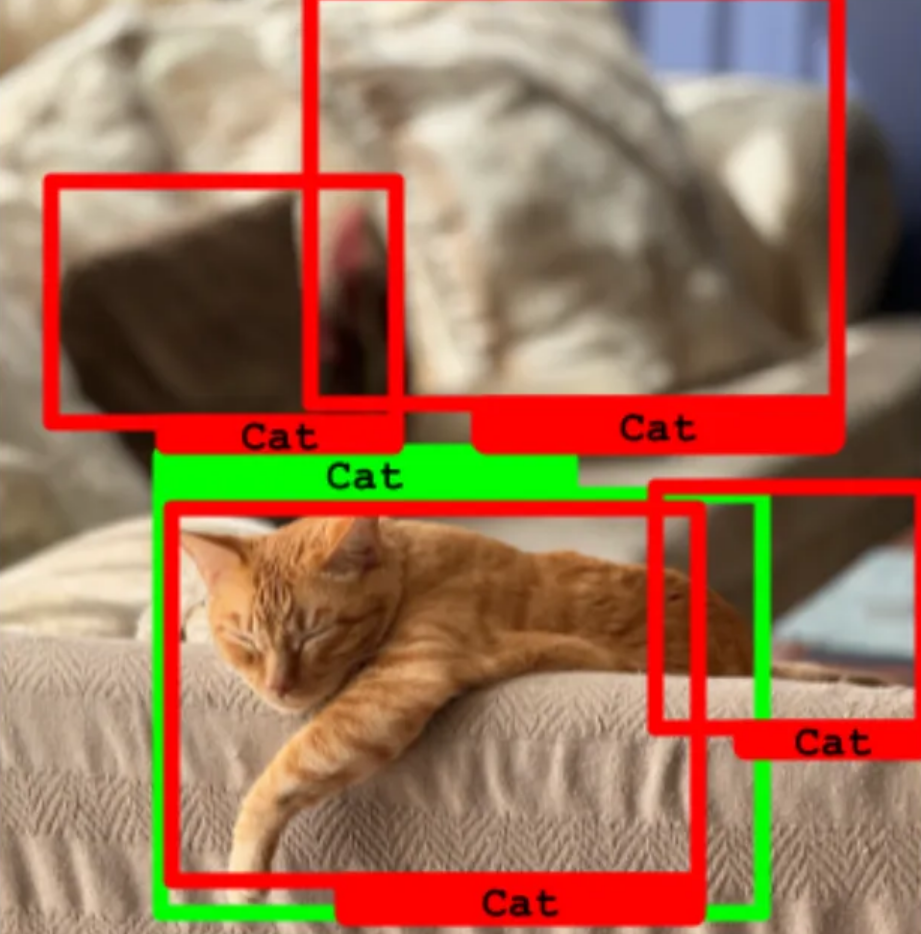
  正如所观察到的，尽管召回率为100%，但模型由于大量假阳性的存在，实际表现较差。
  结论：不应单独评估召回率，因为这种衡量方式未包括假阳性的影响。
  6.3 F1 Score
  F1 Score 是精确率（Precision）和召回率（Recall）的调和平均数，用于综合评估分类模型的性能。F1 Score 在模型的精确率和召回率之间取得平衡，是一个有效的单一指标，尤其在数据类别不平衡的情况下。其计算公式如下：
  F 1 Score = 2 × Precision × Recall Precision + Recall F1 \text{ Score} = 2 \times \frac{\text{Precision} \times \text{Recall}}{\text{Precision} + \text{Recall}} F1 Score=2×Precision+RecallPrecision×Recall
  6.3 Precision-Recall （精确率-召回率，PR）曲线
  至此，我们已经认识到精确度和召回率体现了模型的不同特征。在一些场景下，较高的精确度更有优势；而在其他场景下，则需要较高的召回率。通过调节检测器的目标置信度阈值，可以适当调整这些度量指标。
  实际上，有一种十分便捷的方法能够可视化模型对于特定类别在不同分类阈值下的反应。这种方法就是绘制精确度-召回率曲线，详见下图所示：
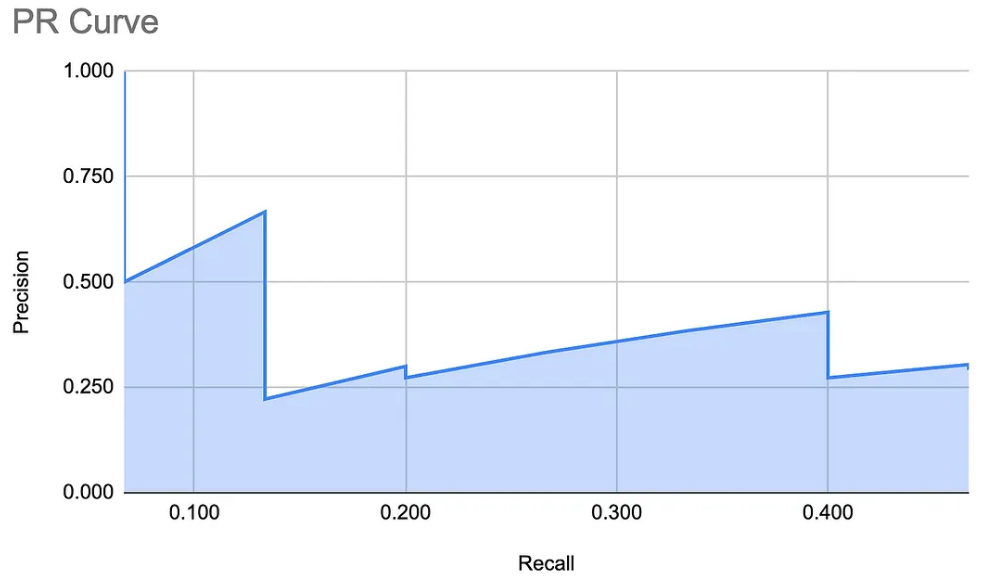
  创建精确率-召回率曲线的具体步骤
  1. 起始点：
    - 将置信度（Confidence Level）设置为 1，这意味着模型只会在非常确定的情况下做出正类预测。
    - 初始精确率（Precision）为 1，因为模型在高置信度下不会有误检（False Positives）。
    - 此时的召回率（Recall）为 0，因为模型可能没有检测到任何实际为正类的样本。
    - 在曲线上标注这一点 (Recall=0, Precision=1)。
      解释此时的召回率（Recall）为 0，置信度为1，表示只有是百分百确定的情况下，才会预测为正类。这样会导致大部分样本识别为反类。按照公式计算，召回率基本到0。可以默认模型可能没有检测到任何实际为正类的样本
    - 降低置信度直到首次检测：
      - 逐渐降低置信度阈值，直到模型首次检测到一个正类样本。
      - 此时的精确率仍为 1，因为没有误检。
      - 计算此时的召回率，并在曲线上标注这一点。
      - 继续降低阈值，直到发生新的检测：
        进一步降低置信度阈值，使得模型检测到更多的正类样本。
        计算新的精确率和召回率，并在曲线上标注相应的点。
        重复这个步骤。
        重复以上步骤，直使得召回率达到 1：
        继续降低阈值，直到所有实际为正类的样本都被模型检测到。
        此时的召回率为 1，精确率可能会降低到接近 0.5（视具体情况而定）。
  代码实现：
```
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import precision_recall_curve, average_precision_score
# 生成数据集
X, y = make_classification(n_samples=1000, n_features=20, random_state=42)
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# 训练逻辑回归模型
model = LogisticRegression()
model.fit(X_train, y_train)
# 预测测试集的概率
y_scores = model.predict_proba(X_test)[:, 1]
# 计算不同阈值下的精确率和召回率
precision, recall, thresholds = precision_recall_curve(y_test, y_scores)
# 计算平均精度
average_precision = average_precision_score(y_test, y_scores)
# 绘制精确率-召回率曲线
plt.figure()
# 逐点绘制精确率-召回率曲线
plt.plot(recall, precision, label=f'Precision-Recall curve (AP={average_precision:.2f})')
# 设置图形标题和标签
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.title('Precision-Recall Curve')
plt.legend(loc='best')
plt.show()
```
  下图显示了在几个特定点评估阈值的精确率-召回率曲线。
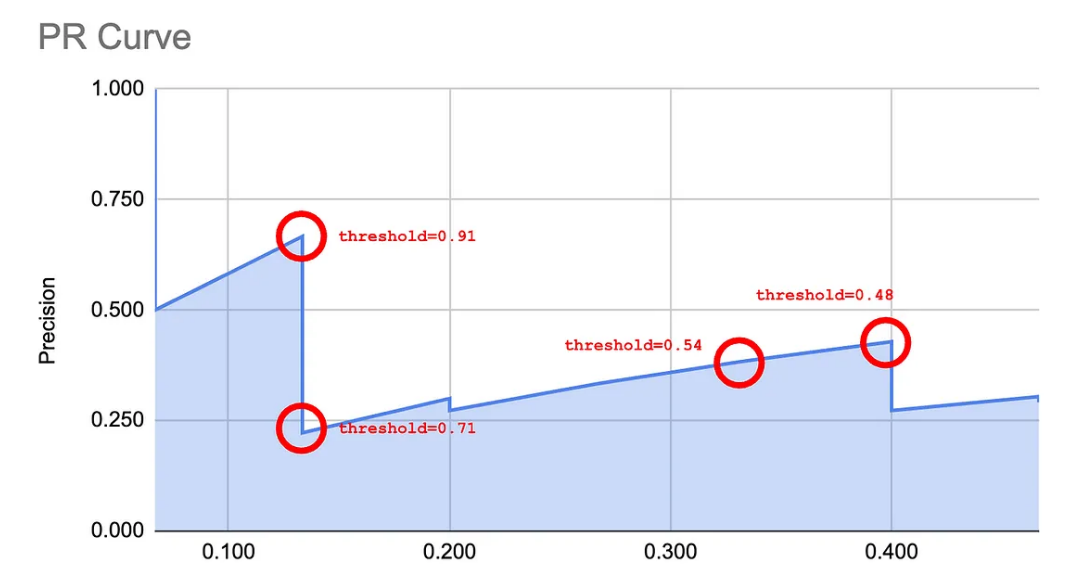
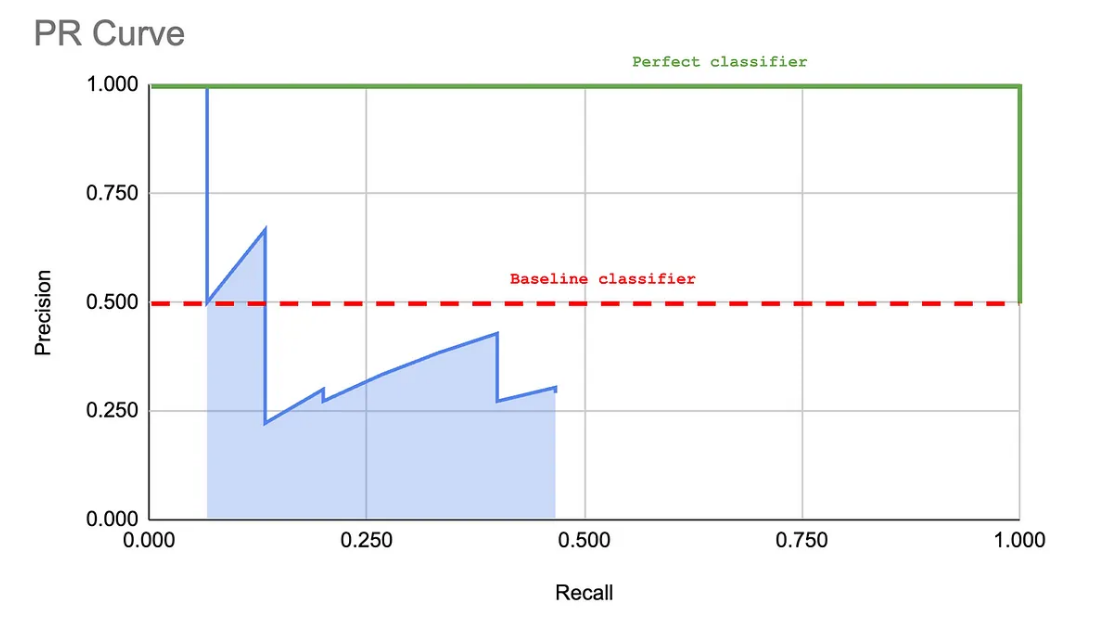
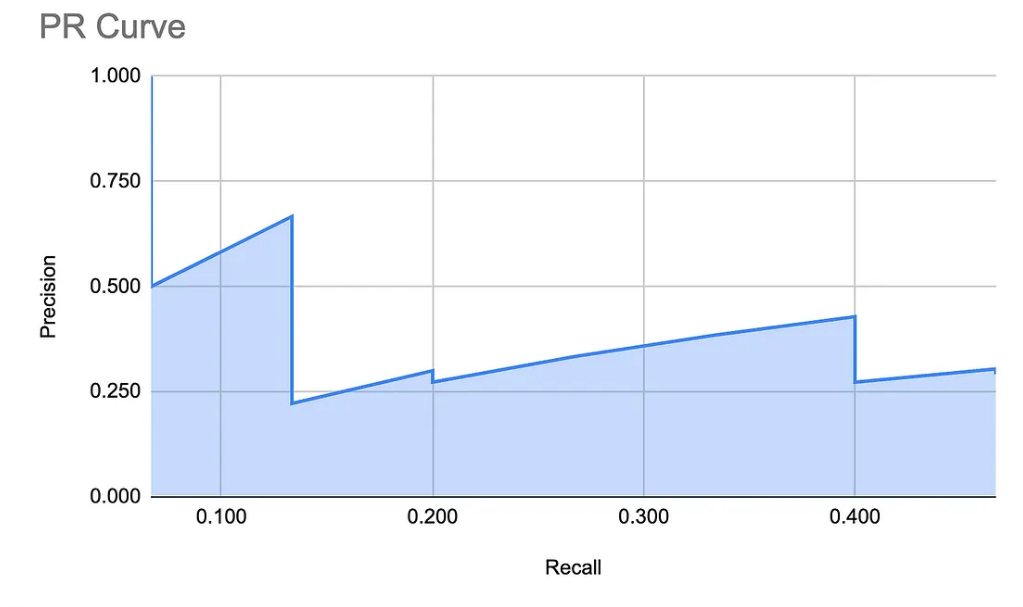
  可以观察到，此曲线的形态能够描述模型的表现。接下来的图形展示了一个“基线”分类器与一个“完美”分类器的对比。分类器越靠近“完美”曲线，其效果越佳。
  更实用的计算PR曲线算法
  事实上，有一个更实用的方法可以计算PR曲线。尽管这看起来可能有些违反直觉，但其结果与之前的步骤相同，只是更加适合脚本操作：
  1. 将所有图像的预测结果根据置信度从高到低进行排序。
  2. 对每一个预测计算真正例（TP）、假正例（FP），以及至此为止的累计真假正例总数。
  3. 使用这些累计数值计算每个预测的精确率和召回率。
  4. 绘制一个显示这些精确率和召回率结果的散点图。
  下表显示了在包含 15 个对象的小型数据集上运行算法的结果：
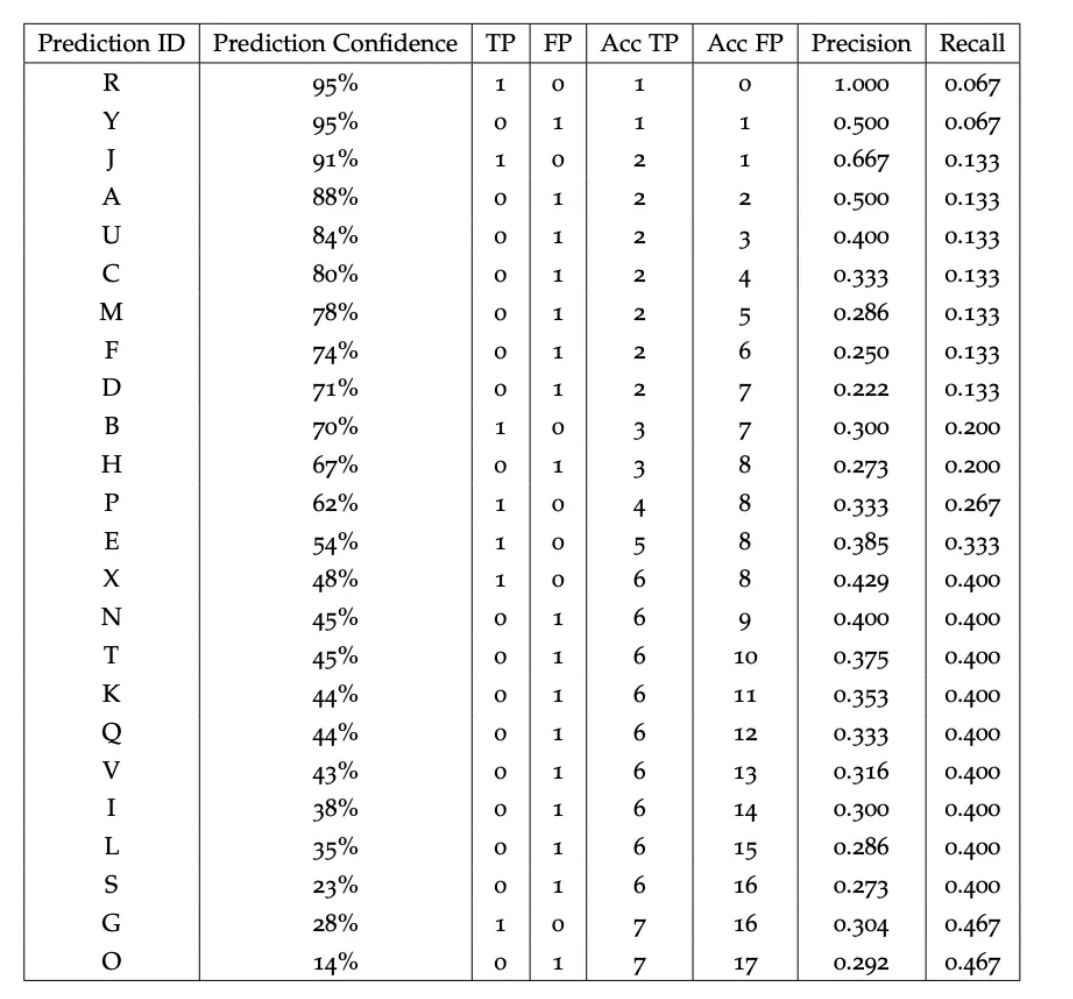
  以一个例子来说明，假设我们需要计算标识符为K的检测结果的精确率和召回率。需要注意的是，数据集中总共有15个真实对象，这意味着真正例和假负例的和为15。
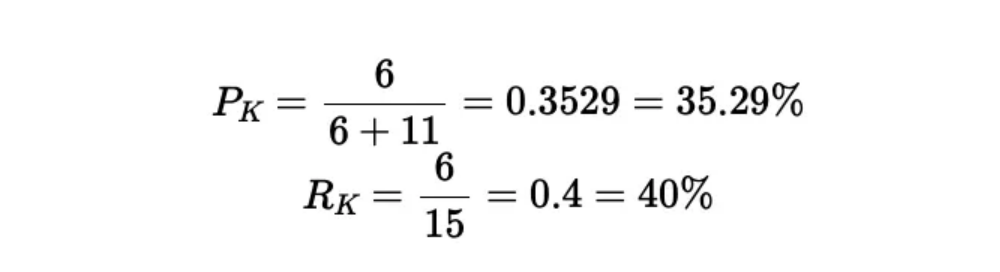
  这里展示的PR曲线（精确率与召回率曲线）是我们之前已经展示过的。为了便于查看，我们再次提供了这个图表：
  7. AP — 平均精确度
  到目前为止，我们已经掌握了为每个类别绘制PR曲线的方法。现在，我们将进行平均精确度的计算。
  平均精度（Average Precision，AP）是用于评估分类模型特别是二分类模型性能的指标。它结合了精确率（Precision）和召回率（Recall）的信息，通过计算在不同阈值下精确率-召回率曲线的面积来衡量模型的性能。
  平均精确度（AP）是指PR曲线（精确率-召回率曲线）下的面积，也称为AUC。
  而，你可能已经注意到，由于PR曲线的不规则形状和尖峰，计算其下的面积相当困难。为此，COCO采用了一种11点插值方法，以简化这一计算过程。
  7.1 COCO11点插值法：COCO 11-Point Interpolation
  给定类别C的11点插值包含三个步骤：
  1. 定义11个等间距的召回评估点：[0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0]。
  2. 对每个召回评估点r，找到所有召回率r’ >= r中的最高精度p。用数学语言表示：
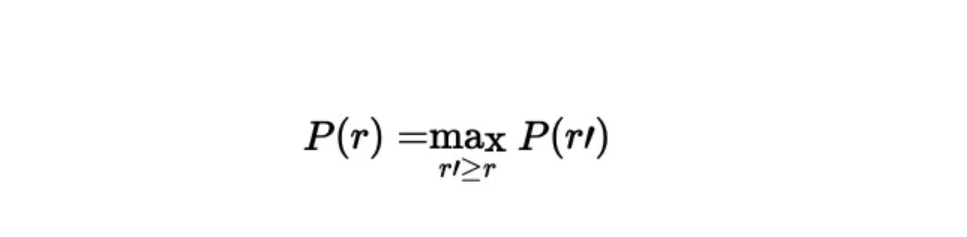
    从图形的角度看，这实际上是一种消除图表中尖峰的方法，效果大致如下：
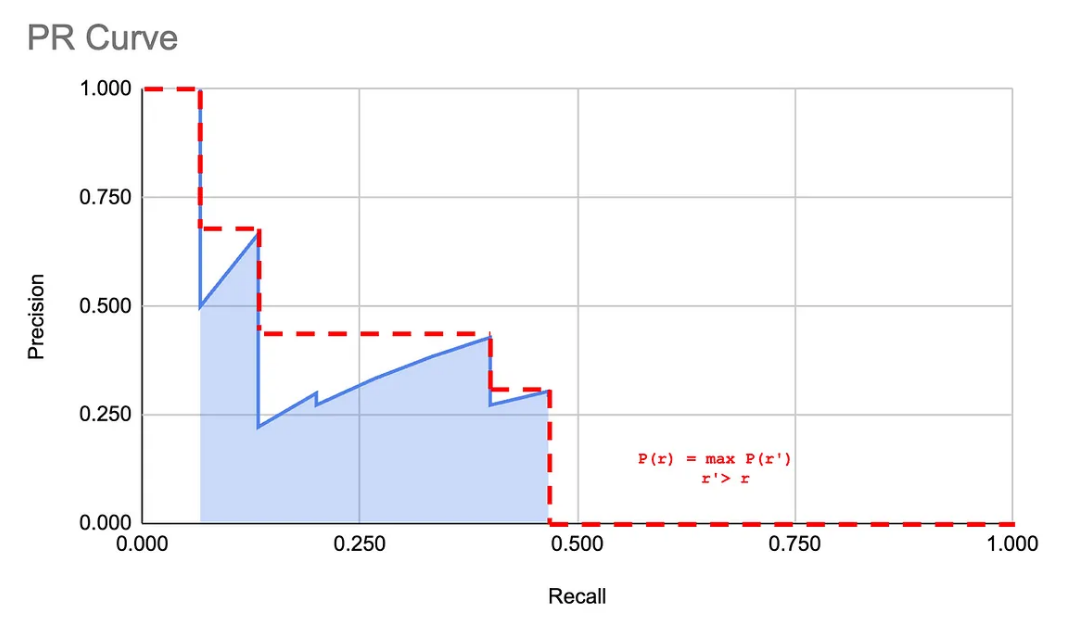
  3. 对这些召回评估点上获得的精度取平均，从而计算出该类别的平均精度AP_C：
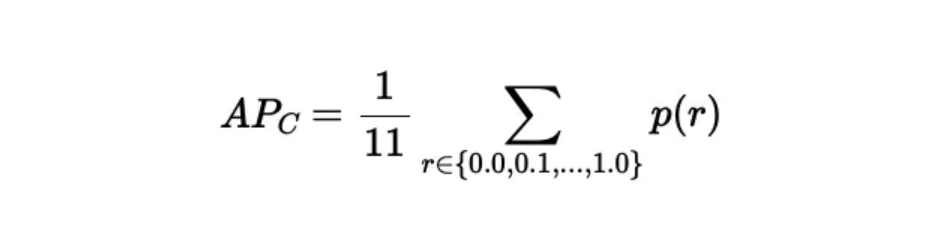
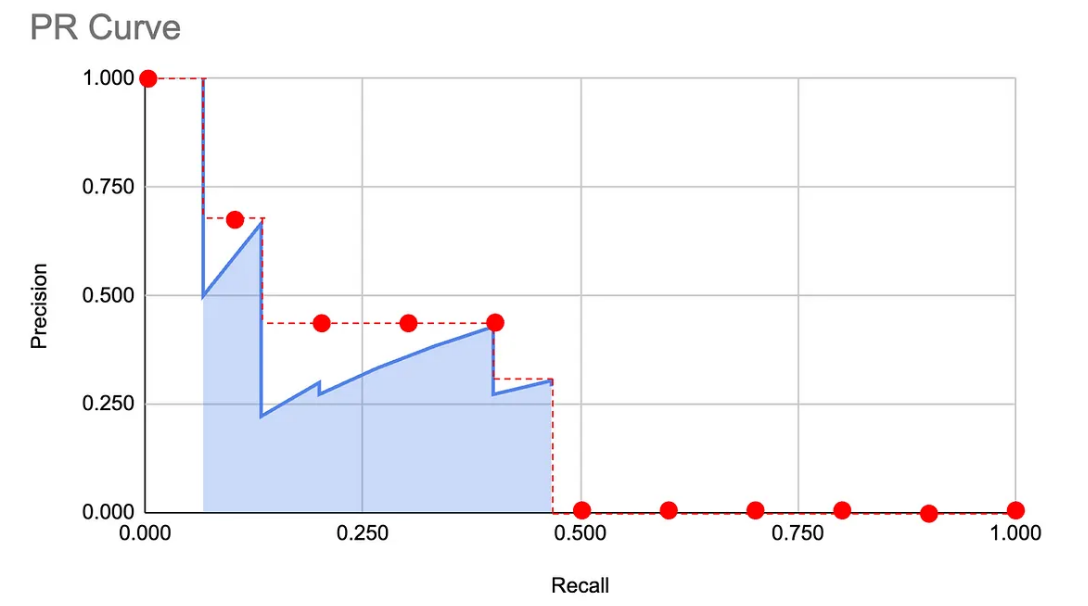
    我们以同一图表为例，来计算平均精度（AP）。
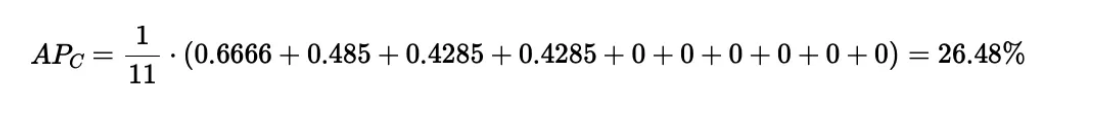
  7.2 代码实现
```
import numpy as np
from sklearn.metrics import precision_recall_curve
from sklearn.metrics import auc
def calculate_11_point_ap(precision, recall):
    """
    Calculate the 11-point interpolated Average Precision (AP) as per the COCO evaluation method.
    """
    recall_levels = np.linspace(0.0, 1.0, 11)
    precision_at_recall = []
    for recall_level in recall_levels:
        precision_values = precision[recall >= recall_level]
        if precision_values.size == 0:
            precision_at_recall.append(0.0)
        else:
            precision_at_recall.append(max(precision_values))
    ap = np.mean(precision_at_recall)
    return ap
# Generate synthetic data (for demonstration purposes)
np.random.seed(42)
y_true = np.random.randint(0, 2, size=1000)
y_scores = np.random.rand(1000)
# Calculate precision-recall pairs for different probability thresholds
precision, recall, _ = precision_recall_curve(y_true, y_scores)
# Calculate the 11-point interpolated AP
ap_11_point = calculate_11_point_ap(precision, recall)
print(f'11-Point Interpolated Average Precision (AP): {ap_11_point:.4f}')
# Plotting Precision-Recall curve
import matplotlib.pyplot as plt
plt.figure()
plt.plot(recall, precision, label=f'Precision-Recall curve (11-Point AP={ap_11_point:.2f})')
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.title('Precision-Recall Curve')
plt.legend(loc='best')
plt.show()
```
  8. COCO mAP — 平均精度均值
  我们终于准备好计算本文重点讨论的指标——mAP了。
  mAP（Mean Average Precision，平均平均精度）是用于评估目标检测模型性能的指标。它结合了所有类别的平均精度（AP），并计算所有类别的平均值。mAP 通常用于多类别目标检测任务，其中每个类别都需要计算单独的 AP，然后求其平均值。
  在上一节中，我们已经为一个特定类别计算了AP。mAP实际上就是所有类别AP的平均值。换言之：
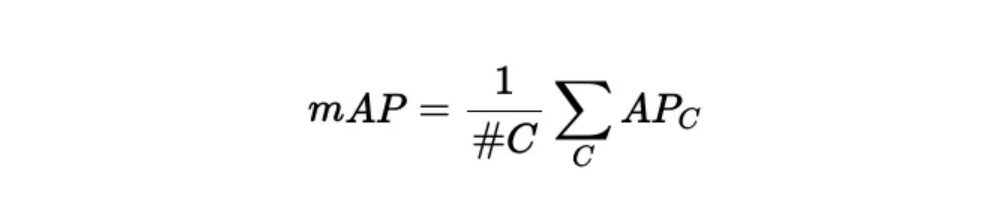
  因此，可以说，mAP是精度的“平均的平均”。接下来，我们将详细介绍前言部分COCO生成的报告内容。
  8.1不同IoU阈值下的mAP
  报告的第一部分如下所示：
```
Average Precision  (AP) @[ IoU=0.50:0.95 | area=   all | maxDets=100 ] = 0.309
Average Precision  (AP) @[ IoU=0.50      | area=   all | maxDets=100 ] = 0.519
Average Precision  (AP) @[ IoU=0.75      | area=   all | maxDets=100 ] = 0.327
```
  术语解释
  - area：评估模型在不同目标大小上的性能，常见的值有 “all”（所有大小），“small”（小目标），“medium”（中等目标），“large”（大目标）。
  - maxDets：评估时允许的最大检测数量，常见值为 1、10 和 100。
    现在让我们专注于 IoU。
    - AP @[ IoU=0.50:0.95 | area= all | maxDets=100 ] = 0.309
      - 这个指标表示在 IoU 从 0.50 到 0.95 的范围内（以 0.05 为步长），所有目标面积（area=all）和最大检测数为 100（maxDets=100）的条件下，模型的平均精度为 0.309。
      - 这是 COCO 基准中的主要评估指标之一，代表整体模型性能，考虑了各种 IoU 阈值。
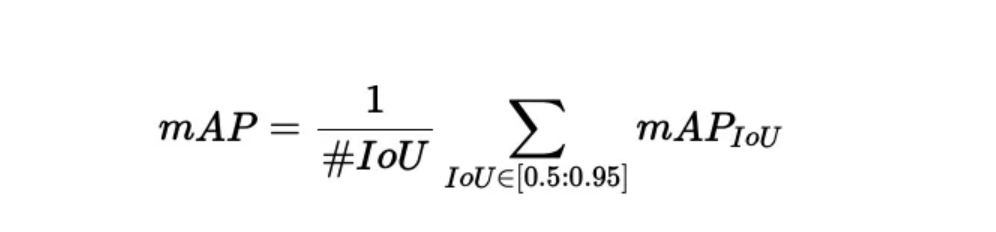
      - AP @[ IoU=0.50 | area= all | maxDets=100 ] = 0.519
        这个指标表示在 IoU 等于 0.50 的条件下，所有目标面积（area=all）和最大检测数为 100（maxDets=100）的条件下，模型的平均精度为 0.519。
        IoU=0.50 是一个较低的阈值，通常被认为是 “宽松” 标准，表示检测框和真实框只需有 50% 的重叠即可视为正确检测。
        AP @[ IoU=0.75 | area= all | maxDets=100 ] = 0.327
        这个指标表示在 IoU 等于 0.75 的条件下，所有目标面积（area=all）和最大检测数为 100（maxDets=100）的条件下，模型的平均精度为 0.327。
        IoU=0.75 是一个较高的阈值，通常被认为是 “严格” 标准，表示检测框和真实框需有 75% 的重叠才视为正确检测。
        8.2 不同物体尺寸的平均精度均值（mAP）
        报告的下一部分内容如下：
        
        Average Precision (AP) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = 0.173 Average Precision (AP) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.462 Average Precision (AP) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.547
        
        让我们现在关注面积部分
        AP @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = 0.173
        这个指标表示在 IoU 从 0.50 到 0.95 的范围内（以 0.05 为步长），小目标面积（area=small）和最大检测数为 100（maxDets=100）的条件下，模型的平均精度为 0.173。
        这个值表示模型在小目标检测上的性能，较低的 AP 值可能表明模型在检测小目标时的性能不太理想。
        AP @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.462
        这个指标表示在 IoU 从 0.50 到 0.95 的范围内（以 0.05 为步长），中等目标面积（area=medium）和最大检测数为 100（maxDets=100）的条件下，模型的平均精度为 0.462。
        这个值表示模型在中等目标检测上的性能，相对较高的 AP 值表明模型在检测中等大小目标时表现较好。
        AP @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.547
        这个指标表示在 IoU 从 0.50 到 0.95 的范围内（以 0.05 为步长），大目标面积（area=large）和最大检测数为 100（maxDets=100）的条件下，模型的平均精度为 0.547。
        这个值表示模型在大目标检测上的性能，较高的 AP 值表明模型在检测大目标时表现较为出色。
        总结
        这些指标分别反映了模型在不同目标大小上的检测性能：
        小目标（small）：模型性能较弱，AP 值较低。
        中等目标（medium）：模型性能良好，AP 值中等。
        大目标（large）：模型性能最佳，AP 值最高。
        小物体的面积范围是 [0², 32²[。
        中物体的面积范围是 [32², 96²[。
        大物体的面积范围是 [96², ∞[，其中，出于实际考虑，∞ 被定义为 1e⁵²。
        8.3 代码实现
        
        import numpy as np from sklearn.metrics import precision_recall_curve, average_precision_score # 假设有3个类别 num_classes = 3 np.random.seed(42) # 生成合成数据 y_true = np.random.randint(0, 2, size=(1000, num_classes)) y_scores = np.random.rand(1000, num_classes) # 计算每个类别的 AP average_precisions = [] for i in range(num_classes): precision, recall, _ = precision_recall_curve(y_true[:, i], y_scores[:, i]) ap = average_precision_score(y_true[:, i], y_scores[:, i]) average_precisions.append(ap) print(f'Class {i} - AP: {ap:.4f}') # 计算 mAP mAP = np.mean(average_precisions) print(f'Mean Average Precision (mAP): {mAP:.4f}')
        
        9. 平均召回率（AR）
        AR（Average Recall，平均召回率）：在不同 IoU 阈值下，模型召回率的平均值。AR 通过计算不同 IoU 阈值下的召回率，然后取平均值得到。
        高 AR：表示模型在各种 IoU 阈值下能够召回大多数的真实目标，漏检率较低，表明模型具有较强的检测能力。
        低 AR：表示模型在各种 IoU 阈值下漏检较多，召回能力较弱，可能需要进一步优化。
        9.1 如何计算 AR
        计算 AR 的步骤如下：
        确定 IoU 阈值：选择一系列 IoU 阈值（例如从 0.50 到 0.95，步长为 0.05），用于评估模型的召回率。
        计算每个 IoU 阈值下的召回率：对于每个 IoU 阈值，计算模型的召回率。
        求平均值：将所有 IoU 阈值下的召回率取平均值，即为 AR。
        假设有以下召回率数据：
        IoU = 0.50 时，召回率 = 0.75
        IoU = 0.55 时，召回率 = 0.74
        …
        IoU = 0.95 时，召回率 = 0.60
        将这些召回率值相加后取平均值，即为 AR。
        下面是报告中的最后一部分：
        
        Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets= 1 ] = 0.297 Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets= 10 ] = 0.456 Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets=100 ] = 0.511
        
        这三个平均召回率（AR）指标分别表示在不同的最大检测数（maxDets）限制下，模型在给定 IoU 阈值范围和所有目标面积（area=all）上的召回能力。以下是对每个指标的详细解读：
        Average Recall (AR) @[ IoU=0.50:0.95 | area=all | maxDets=1 ] = 0.297
        IoU范围：0.50 到 0.95，以 0.05 为步长。
        目标面积：所有目标（small, medium, large）。
        最大检测数：1，即每张图像最多只考虑一个检测框。
        AR 值：0.297。
        解读：在只允许每张图像最多检测一个目标的情况下，模型的平均召回率为 0.297。这表示模型在这种严格限制下漏检较多，只能召回约 29.7% 的真实目标。
        Average Recall (AR) @[ IoU=0.50:0.95 | area=all | maxDets=10 ] = 0.456
        IoU范围：0.50 到 0.95，以 0.05 为步长。
        目标面积：所有目标（small, medium, large）。
        最大检测数：10，即每张图像最多考虑十个检测框。
        AR 值：0.456。
        解读：在允许每张图像最多检测十个目标的情况下，模型的平均召回率为 0.456。这表示模型在这种限制下能够召回约 45.6% 的真实目标，漏检率有所减少，检测性能有所提高。
        Average Recall (AR) @[ IoU=0.50:0.95 | area=all | maxDets=100 ] = 0.511
        IoU范围：0.50 到 0.95，以 0.05 为步长。
        目标面积：所有目标（small, medium, large）。
        最大检测数：100，即每张图像最多考虑一百个检测框。
        AR 值：0.511。
        解读：在允许每张图像最多检测一百个目标的情况下，模型的平均召回率为 0.511。这表示模型在这种较宽松的限制下能够召回约 51.1% 的真实目标，漏检率进一步减少，检测性能较好。
        COCO 评估 API
        至此，希望你已经明白了不同版本的mAP的计算方式，更重要的是，了解它们各自的含义。COCO提供了一个Python模块，该模块能够在计算所有这些指标.
        
        # 导入所需库以下载示例数据集 import requests import zipfile from tqdm import tqdm # 导入一个示例模型 from ultralytics import YOLO # 导入COCO工具 from pycocotools.coco import COCO from pycocotools.cocoeval import COCOeval # 导入库以检查是否需要重新下载 import os # 定义一个辅助函数以下载文件 def download_file(url, file_path): # 发起HTTP GET请求以流式下载文件 response = requests.get(url, stream=True) # 获取文件的总大小（字节数） total_size_in_bytes = int(response.headers.get('content-length', 0)) # 定义块大小为1024字节（1 Kibibyte） block_size = 1024 # 初始化进度条 progress_bar = tqdm(total=total_size_in_bytes, unit='iB', unit_scale=True) # 以二进制写入模式打开目标文件 with open(file_path, 'wb') as file: # 分块写入文件内容 for data in response.iter_content(block_size): # 更新进度条 progress_bar.update(len(data)) # 写入数据块到文件 file.write(data) # 关闭进度条 progress_bar.close() # COCO数据集的下载链接和目标路径 coco_url = "https://github.com/ultralytics/yolov5/releases/download/v1.0/coco2017val.zip" coco_zip_path = 'coco2017val.zip' # 仅在coco目录不存在时下载并解压文件 if not os.path.exists('coco'): # 下载COCO数据集 download_file(coco_url, coco_zip_path) # 解压下载的zip文件 with zipfile.ZipFile(coco_zip_path, 'r') as zip_ref: zip_ref.extractall('.') # 加载预训练的YOLOv8模型 model = YOLO('./yolov8n.pt') # 加载COCO验证集图像的标注文件 coco_annotations_path = 'coco/annotations/instances_val2017.json' coco = COCO(coco_annotations_path) # 获取图像的ID列表 image_ids = coco.getImgIds() # 根据图像ID加载图像信息 images = coco.loadImgs(image_ids) # 处理图像并收集检测结果 results = [] for img in images: # 获取图像路径 image_path = f"coco/images/val2017/{img['file_name']}" # 使用模型进行预测 preds = model(image_path)[0].numpy().boxes # 将预测结果转换为COCO兼容的格式 for xyxy, conf, cls in zip(preds.xyxy, preds.conf, preds.cls): result = { 'image_id': img['id'], 'category_id': int(cls.item() + 1), # 类别ID从0开始，因此需要+1 'bbox': [xyxy[0].item(), xyxy[1].item(), xyxy[2].item() - xyxy[0].item(), xyxy[3].item() - xyxy[1].item()], # 计算宽和高 'score': conf.item() # 置信度得分 } # 将结果添加到结果列表 results.append(result) # 将结果转换为COCO格式对象 coco_dt = coco.loadRes(results) # 运行COCO评估 coco_eval = COCOeval(coco, coco_dt, 'bbox') coco_eval.evaluate() # 评估 coco_eval.accumulate() # 累积结果 coco_eval.summarize() # 汇总并打印评估结果
        
        运行脚本会得到下面的结果：
        
        Average Precision (AP) @[ IoU=0.50:0.95 | area= all | maxDets=100 ] = 0.053 Average Precision (AP) @[ IoU=0.50 | area= all | maxDets=100 ] = 0.071 Average Precision (AP) @[ IoU=0.75 | area= all | maxDets=100 ] = 0.058 Average Precision (AP) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = 0.021 Average Precision (AP) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.052 Average Precision (AP) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.083 Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets= 1 ] = 0.043 Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets= 10 ] = 0.061 Average Recall (AR) @[ IoU=0.50:0.95 | area= all | maxDets=100 ] = 0.061 Average Recall (AR) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = 0.027 Average Recall (AR) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.062 Average Recall (AR) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.094
        
        总结
        IoU是衡量边界框预测准确性的指标。
        IoU可作为决定是否舍弃或接受预测的阈值。
        依据IoU，对象检测器为每类定义了真阳性（TP）、假阳性（FP）、真阴性（TN）和假阴性（FN）。
        通过这些定义和IoU，我们能计算出检测器每个类别的精确度、召回率和F1得分。
        精确度衡量对某类预测中准确的占比。
        召回率衡量对于给定类别中的所有对象，有多少百分比被准确预测。
        单独衡量精确度和召回率可能会导致误解。
        F1得分平衡了精确度与召回率。
        PR曲线的形状和曲线下面积展示了检测器对于特定类别的性能。
        PR曲线的插值可以消除曲线的波峰。
        COCO通过在11个等距召回点上评估插值曲线的AP值。
        mAP是所有类别AP值的平均。
        mAP为不同情况下检测器的性能提供度量。
        COCOEval是计算Python脚本中COCO mAP的API。