【C++进阶06】红黑树图文详解及C++模拟实现红黑树，C++进阶，红黑树图文详解与模拟实现指南，C++进阶，红黑树图文详解与模拟实现指南

摘要：本内容主要介绍了红黑树的图文详解及C++模拟实现指南。作为C++进阶的重要内容之一，红黑树是一种平衡二叉搜索树，具有优秀的查找、插入和删除性能。本文通过图文结合的方式，详细讲解了红黑树的原理、性质和实现方法，并提供了C++模拟实现的指南，帮助读者更好地理解和掌握红黑树的相关知识。

红黑树的平衡性质

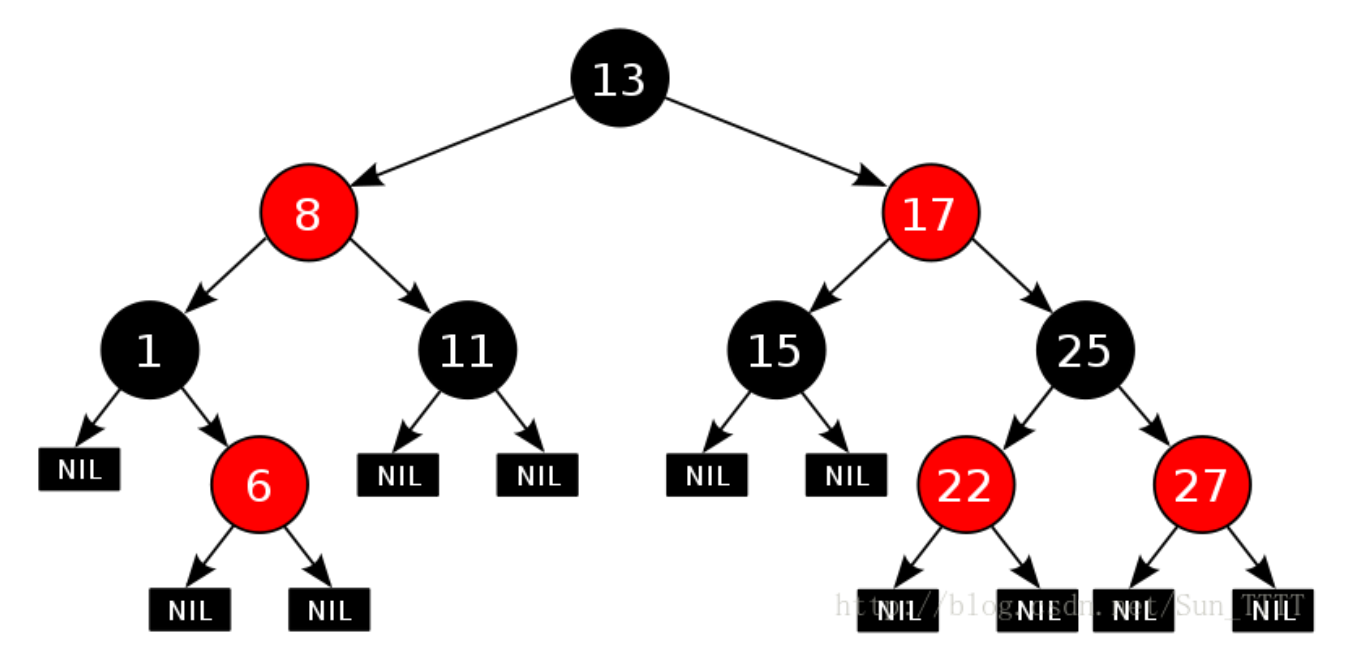
红黑树的核心特性是其平衡性质，保证了树的高度在log(N)级别，从而确保了查找、插入和删除操作的效率，红黑树的平衡性质体现在其节点颜色的规则和树的结构上，每个节点要么是红色要么是黑色，需满足以下性质：

1、每个叶子节点（NIL节点，空节点）是黑色的。

2、每个红色节点的两个子节点都是黑色的，即从每个叶子节点到根的所有路径上不能有两个连续红色节点。

3、从任一节点到其每个叶子的所有简单路径都包含相同数量的黑色节点，这些性质确保了红黑树在插入和删除节点后仍然保持平衡。

红黑树的插入操作

在插入新节点后，除了需要调整颜色以满足红黑树的性质外，还需要对新插入的节点进行旋转操作以确保树的形状满足红黑树的定义，旋转操作包括左旋和右旋，用于调整树的结构以满足红黑树的性质，在插入新节点后，可能需要进行多次旋转和颜色调整操作，以确保树仍然满足红黑树的性质。

红黑树的删除操作

除了插入操作，红黑树的删除操作也是其重要的部分，删除操作涉及到查找要删除的节点、更新节点的颜色以及进行旋转操作来保持树的平衡，删除操作同样需要满足红黑树的性质，可能需要调整节点的颜色和进行旋转操作。

红黑树的应用场景

红黑树是一种自平衡的二叉搜索树，广泛应用于需要频繁进行查找、插入和删除操作的场景，它适用于操作系统、数据库管理系统、网络路由等领域，用于维护数据的顺序和快速查找。

代码实现说明

你提供的代码实现部分已经相对完整，在实际应用中，还需要考虑错误处理、边界情况的处理等因素，为了代码的健壮性和可维护性，建议添加注释、文档和测试代码来验证实现的正确性，实现过程中应注意代码的清晰性和可读性，以便于他人理解和维护。

在实际应用中，除了红黑树的基本操作外，还可能涉及到其他相关内容，可以考虑研究其他自平衡二叉搜索树（如AVL树）的特性及实现方式，以了解不同数据结构的特点和适用场景，还可以探索红黑树在其他领域的应用，如计算机图形学、人工智能等。

希望这些补充内容能对你有所帮助！如果你还有其他问题或需要进一步的解释，请随时提问。