摘要:,,本文探讨了基于Matlab的多目标规划算法实现与优化策略。通过优化模型,结合多目标规划的特点,对算法进行实现与策略优化。文章介绍了如何在Matlab中实现多目标规划算法,并探究了优化策略,以提高算法效率和求解质量。对于解决复杂优化问题,本文提供了一种有效的方法和思路。
随着科技的发展,多目标规划问题在各个领域的应用越来越广泛,本文将介绍多目标规划的基本概念、数学模型以及求解方法,并通过案例分析,详细阐述如何使用MATLAB软件进行多目标规划模型的构建和求解。
多目标规划概述
多目标规划是一种数学优化方法,旨在同时优化多个目标函数,这些目标函数通常是相互矛盾的,多目标规划的目标是在满足一系列约束条件下,找到一组解,使得各个目标函数都能取得最优值。

多目标规划的数学模型
对于多个目标函数f1, f2, ..., fm,带有多个约束条件的多目标规划的一般形式为:
min/max F(x) = (f1(x), f2(x), ..., fm(x))
s.t. gi(x) ≤ 0, i = 1, ..., p
hj(x) = 0, j = 1, ..., q
lb ≤ x ≤ ub
F(x)是向量目标函数,gi(x)是不等式约束,hj(x)是等式约束,lb和ub分别是变量的上下界。

多目标规划的求解方法
常见的多目标规划求解方法包括加权法、序贯法、NSGA-II等,本文将主要介绍加权法,即将多目标问题转化为单目标问题的求解方法,具体地,通过引入权重因子,将多个目标函数加权求和,得到一个单一的目标函数,然后按照单目标优化问题的方法求解。
案例分析
考虑以下多目标线性规划问题:
max Z1 = 100x1 + 90x2 + 80x3 + 70x4
min Z2 = 3x2 + 2x4
s.t. 一系列线性约束条件...
使用MATLAB软件,我们可以方便地求解该多目标规划问题,得到最优解和最优值。
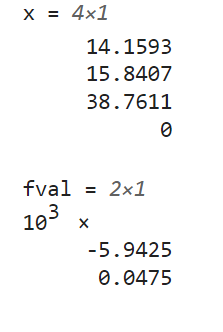
MATLAB代码实现
(在此处插入具体的MATLAB代码)
求解结果与分析
在约束条件下,只考虑第一个目标函数时,最优解为...;只考虑第二个目标函数时,最优解为...,若考虑两个目标同样重要,则通过加权法求得的多目标规划的最优解和最优值分别为...,通过对求解结果的分析,我们可以为实际工程设计和决策过程提供有力的支持。
本文详细介绍了多目标规划的基本概念、数学模型以及求解方法,并通过案例分析,阐述了如何使用MATLAB软件进行多目标规划模型的构建和求解,随着人工智能和大数据技术的发展,多目标规划问题将在更多领域得到应用,我们可以进一步研究多目标规划与其他优化方法的结合,以解决实际工程中遇到的复杂问题。






还没有评论,来说两句吧...