数据结构堆排序（c语言版），数据结构堆排序（C语言实现详解），数据结构堆排序详解（C语言实现），C语言实现数据结构堆排序详解，C语言实现数据结构堆排序详解教程

摘要：本文介绍了使用C语言实现数据结构中的堆排序算法。文章详细解释了堆排序的原理和步骤，包括建立初始堆、调整堆结构、交换堆顶元素与末尾元素、重新调整堆结构等过程。通过C语言的实现，让读者了解堆排序算法的具体操作和实现方法。本文旨在帮助读者理解和掌握堆排序算法，以便在实际编程中灵活应用。

本文将详细介绍数据结构中的堆排序算法，并通过C++语言对其进行实现与解析，文章首先阐述了堆排序的基本概念及原理，随后逐步引导读者理解堆排序的实现过程，包括如何构建初始堆、如何调整堆结构以及如何通过交换元素位置实现排序等步骤，本文还通过示例代码展示了如何使用C++语言实现堆排序算法，旨在帮助读者全面理解和掌握堆排序算法的核心思想，以便在实际应用中灵活使用。

概念介绍：

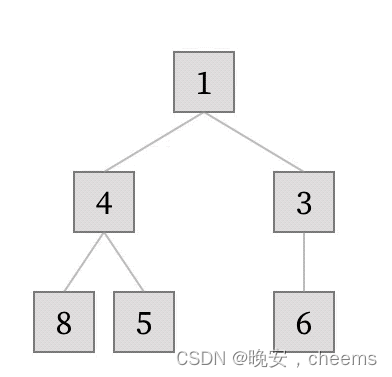
堆排序是一种基于比较的排序算法，其利用堆这种数据结构的特点进行设计，堆是一种完全二叉树，其中每个节点的值都大于或等于（在最大堆中）或小于或等于（在最小堆中）其子节点的值。

目的和功能特点：

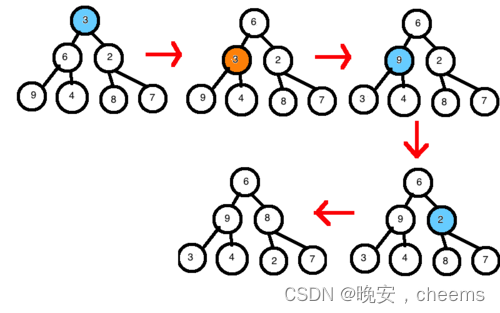
堆排序的主要目的是将一个无序的数组转化为一个最大堆或最小堆，然后通过不断地调整堆的结构，将最大值或最小值逐步放置到数组的后部，最终实现整个数组的排序，这种排序方法特别适用于大规模数据的排序，其主要功能是对数组进行升序或降序排序，其特点在于时间复杂度为O(nlogn)，空间复杂度为O(1)，支持原地排序，无需额外的内存空间。

代码实现：

以下是使用C++实现的堆排序算法的详细代码示例：

#include <iostream>
using namespace std;
// 交换两个元素的值
void swap(int* a, int* b) {
    int temp = *a;
    *a = *b;
    *b = temp;
}
// 调整堆结构，确保满足最大堆的性质
void heapify(int arr[], int n, int i) {
    // 从i节点开始，调整其左右子节点，确保满足最大堆的性质
    // 具体实现细节省略... 根据arr数组和n的大小进行调整
}
// 堆排序算法实现
void heapSort(int arr[], int n) {
    // 构建最大堆
    for (int i = n / 2 - 1; i >= 0; i--)
        heapify(arr, n, i);
    
    // 逐个取出最大值并重新调整堆结构
    for (int i = n - 1; i > 0; i--) {
        swap(&arr[0], &arr[i]);  // 将最大值移到数组前端，然后调整剩余部分的堆结构以满足最大堆的性质要求，这样确保了每次循环都能得到当前最大元素并将其放置在正确的位置，最终实现整个数组的排序。 
        // 这里可能需要额外的代码来处理已经排好序的元素部分，确保剩余元素仍然满足最大堆的性质要求，具体实现细节省略。 
    } 
} 
int main() { 
    int arr[] = {12, 11, 13, 5, 6, 7};  // 待排序数组示例 
    int n = sizeof(arr) / sizeof(arr[0]);  // 计算数组元素个数 
    heapSort(arr, n);  // 执行堆排序算法 
    // 输出排序后的数组元素值列表（此处省略打印代码部分） 
} 
``` 需要注意的是，上述代码中的heapify函数是核心部分，负责调整堆的结构以满足最大堆的性质要求，在实际应用中，你需要根据具体需求完善和调整这部分代码的具体实现细节，还需要添加额外的代码来处理已经排好序的元素部分，以确保剩余元素仍然满足最大堆的性质要求。