MATLAB 支持向量机（SVM），MATLAB中的支持向量机（SVM）应用，MATLAB中的支持向量机（SVM）应用与实践

摘要：MATLAB支持向量机（SVM）是一种广泛应用于机器学习领域的分类算法。在MATLAB环境中，SVM可用于数据分类、回归分析和异常检测等任务。通过构建超平面来分隔数据，SVM能够处理非线性数据并具有良好的泛化能力。在MATLAB中，SVM的使用简便，高效，为数据分析提供了强大的工具。

MATLAB支持向量机（SVM）简介

支持向量机（SVM）是一种基于统计学习理论的强大分类与回归方法，它通过构建超平面来分隔数据，利用训练数据中的样本点定义决策边界，并最大化不同类别之间的分隔距离，在机器学习和数据科学领域，SVM占有重要地位，广泛应用于图像识别、文本分类、手写数字识别等领域。

基础概念

SVM是一种监督学习模型，主要用于分类和回归分析，在SVM模型中，数据被划分到不同的类别中，每个类别都由一个超平面分隔，这些超平面是通过模型学习得到的，目的是最大化不同类别之间的间隔，称为最大间隔超平面。

线性可分情况

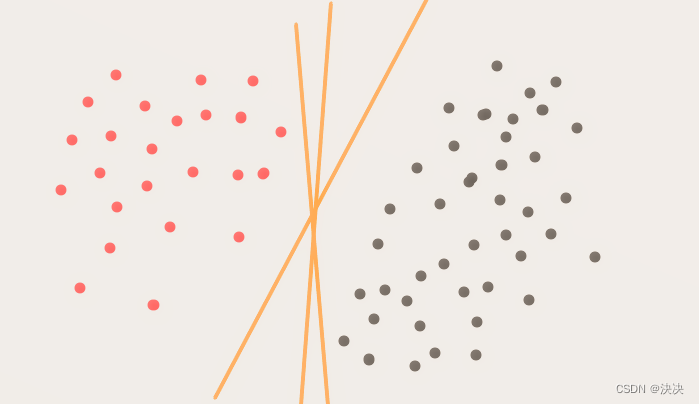
在简单的线性可分情况下，假设我们有一个二维数据集，两个类别的数据点可以通过一条直线（即超平面）进行分隔，对于非线性可分的数据，SVM会使用核方法将其映射到更高维的空间，以找到一个分隔超平面。

二分类问题

在二分类问题中，我们只有一个正类和一个负类。fitcsvm函数用于训练SVM模型，通过计算每个样本到超平面的距离来预测新样本的类别。

非线性及多分类问题

对于非线性可分的数据，可以使用核方法（如RBF核）来处理，对于多分类问题，常用的策略是一对多（one-versus-rest）的方法，其中每个类别都被视为一个独立的二分类问题，综合多个二分类器的结果来确定最终类别。

详细解释

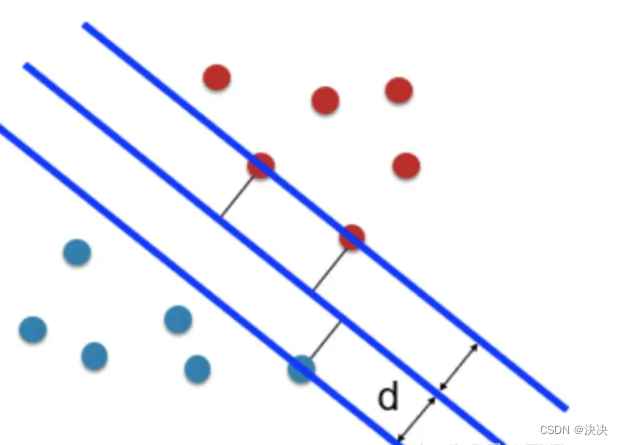
除了上述基本介绍，SVM还有以下值得深入了解的方面：

1、核函数：介绍不同的核函数（如线性核、多项式核、RBF核等）及其应用场景，选择合适的核函数对于SVM模型的性能至关重要。

2、参数选择：讨论如何选择适当的参数（如C、gamma等）以优化SVM模型，这些参数的选择对模型的泛化能力有很大影响。

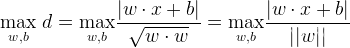
3、软间隔与硬间隔：解释软间隔SVM和硬间隔SVM的区别及应用场景，在现实世界的数据集中，往往存在噪声或异常值，软间隔SVM能更好地处理这些情况。

4、过拟合与欠拟合：讨论SVM模型中的过拟合和欠拟合问题，以及如何通过交叉验证、调整模型复杂度等方法来解决这些问题。

5、实例演示：提供实际的数据集，展示如何使用MATLAB进行SVM模型的训练、预测及性能评估，通过实例，让读者更好地理解和掌握SVM的应用。

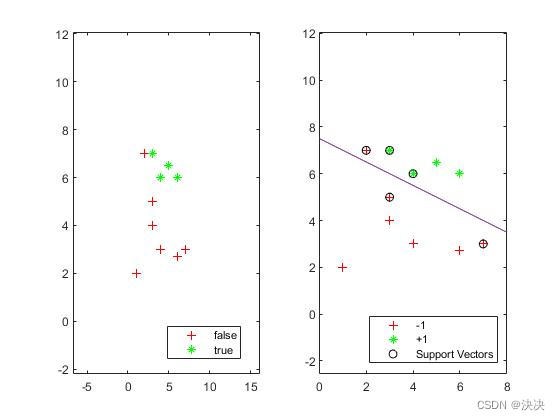
通过这篇解释和代码示例，读者可以全面了解SVM的基本原理、应用场景和实现方法，希望这些内容对读者有所帮助！